
- DSA - Home
- DSA - Overview
- DSA - Environment Setup
- DSA - Algorithms Basics
- DSA - Asymptotic Analysis
- Data Structures
- DSA - Data Structure Basics
- DSA - Data Structures and Types
- DSA - Array Data Structure
- DSA - Skip List Data Structure
- Linked Lists
- DSA - Linked List Data Structure
- DSA - Doubly Linked List Data Structure
- DSA - Circular Linked List Data Structure
- Stack & Queue
- DSA - Stack Data Structure
- DSA - Expression Parsing
- DSA - Queue Data Structure
- DSA - Circular Queue Data Structure
- DSA - Priority Queue Data Structure
- DSA - Deque Data Structure
- Searching Algorithms
- DSA - Searching Algorithms
- DSA - Linear Search Algorithm
- DSA - Binary Search Algorithm
- DSA - Interpolation Search
- DSA - Jump Search Algorithm
- DSA - Exponential Search
- DSA - Fibonacci Search
- DSA - Sublist Search
- DSA - Hash Table
- Sorting Algorithms
- DSA - Sorting Algorithms
- DSA - Bubble Sort Algorithm
- DSA - Insertion Sort Algorithm
- DSA - Selection Sort Algorithm
- DSA - Merge Sort Algorithm
- DSA - Shell Sort Algorithm
- DSA - Heap Sort Algorithm
- DSA - Bucket Sort Algorithm
- DSA - Counting Sort Algorithm
- DSA - Radix Sort Algorithm
- DSA - Quick Sort Algorithm
- Matrices Data Structure
- DSA - Matrices Data Structure
- DSA - Lup Decomposition In Matrices
- DSA - Lu Decomposition In Matrices
- Graph Data Structure
- DSA - Graph Data Structure
- DSA - Depth First Traversal
- DSA - Breadth First Traversal
- DSA - Spanning Tree
- DSA - Topological Sorting
- DSA - Strongly Connected Components
- DSA - Biconnected Components
- DSA - Augmenting Path
- DSA - Network Flow Problems
- DSA - Flow Networks In Data Structures
- DSA - Edmonds Blossom Algorithm
- DSA - Maxflow Mincut Theorem
- Tree Data Structure
- DSA - Tree Data Structure
- DSA - Tree Traversal
- DSA - Binary Search Tree
- DSA - AVL Tree
- DSA - Red Black Trees
- DSA - B Trees
- DSA - B+ Trees
- DSA - Splay Trees
- DSA - Range Queries
- DSA - Segment Trees
- DSA - Fenwick Tree
- DSA - Fusion Tree
- DSA - Hashed Array Tree
- DSA - K-Ary Tree
- DSA - Kd Trees
- DSA - Priority Search Tree Data Structure
- Recursion
- DSA - Recursion Algorithms
- DSA - Tower of Hanoi Using Recursion
- DSA - Fibonacci Series Using Recursion
- Divide and Conquer
- DSA - Divide and Conquer
- DSA - Max-Min Problem
- DSA - Strassen's Matrix Multiplication
- DSA - Karatsuba Algorithm
- Greedy Algorithms
- DSA - Greedy Algorithms
- DSA - Travelling Salesman Problem (Greedy Approach)
- DSA - Prim's Minimal Spanning Tree
- DSA - Kruskal's Minimal Spanning Tree
- DSA - Dijkstra's Shortest Path Algorithm
- DSA - Map Colouring Algorithm
- DSA - Fractional Knapsack Problem
- DSA - Job Sequencing with Deadline
- DSA - Optimal Merge Pattern Algorithm
- Dynamic Programming
- DSA - Dynamic Programming
- DSA - Matrix Chain Multiplication
- DSA - Floyd Warshall Algorithm
- DSA - 0-1 Knapsack Problem
- DSA - Longest Common Sub-sequence Algorithm
- DSA - Travelling Salesman Problem (Dynamic Approach)
- Hashing
- DSA - Hashing Data Structure
- DSA - Collision In Hashing
- Disjoint Set
- DSA - Disjoint Set
- DSA - Path Compression And Union By Rank
- Heap
- DSA - Heap Data Structure
- DSA - Binary Heap
- DSA - Binomial Heap
- DSA - Fibonacci Heap
- Tries Data Structure
- DSA - Tries
- DSA - Standard Tries
- DSA - Compressed Tries
- DSA - Suffix Tries
- Treaps
- DSA - Treaps Data Structure
- Bit Mask
- DSA - Bit Mask In Data Structures
- Bloom Filter
- DSA - Bloom Filter Data Structure
- Approximation Algorithms
- DSA - Approximation Algorithms
- DSA - Vertex Cover Algorithm
- DSA - Set Cover Problem
- DSA - Travelling Salesman Problem (Approximation Approach)
- Randomized Algorithms
- DSA - Randomized Algorithms
- DSA - Randomized Quick Sort Algorithm
- DSA - Karger’s Minimum Cut Algorithm
- DSA - Fisher-Yates Shuffle Algorithm
- Miscellaneous
- DSA - Infix to Postfix
- DSA - Bellmon Ford Shortest Path
- DSA - Maximum Bipartite Matching
- DSA Useful Resources
- DSA - Questions and Answers
- DSA - Selection Sort Interview Questions
- DSA - Merge Sort Interview Questions
- DSA - Insertion Sort Interview Questions
- DSA - Heap Sort Interview Questions
- DSA - Bubble Sort Interview Questions
- DSA - Bucket Sort Interview Questions
- DSA - Radix Sort Interview Questions
- DSA - Cycle Sort Interview Questions
- DSA - Quick Guide
- DSA - Useful Resources
- DSA - Discussion
Binary Search Tree
A Binary Search Tree (BST) is a tree in which all the nodes follow the below-mentioned properties −
The left sub-tree of a node has a key less than or equal to its parent node's key.
The right sub-tree of a node has a key greater than or equal to its parent node's key.
Thus, BST divides all its sub-trees into two segments; the left sub-tree and the right sub-tree and can be defined as −
left_subtree (keys) ≤ node (key) ≤ right_subtree (keys)
Binary Tree Representation
BST is a collection of nodes arranged in a way where they maintain BST properties. Each node has a key and an associated value. While searching, the desired key is compared to the keys in BST and if found, the associated value is retrieved.
Following is a pictorial representation of BST −
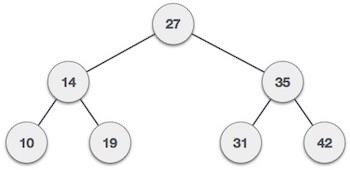
We observe that the root node key (27) has all less-valued keys on the left sub-tree and the higher valued keys on the right sub-tree.
Basic Operations
Following are the basic operations of a Binary Search Tree −
Search − Searches an element in a tree.
Insert − Inserts an element in a tree.
Pre-order Traversal − Traverses a tree in a pre-order manner.
In-order Traversal − Traverses a tree in an in-order manner.
Post-order Traversal − Traverses a tree in a post-order manner.
Defining a Node
Define a node that stores some data, and references to its left and right child nodes.
struct node {
int data;
struct node *leftChild;
struct node *rightChild;
};
Search Operation
Whenever an element is to be searched, start searching from the root node. Then if the data is less than the key value, search for the element in the left subtree. Otherwise, search for the element in the right subtree. Follow the same algorithm for each node.
Algorithm
1. START 2. Check whether the tree is empty or not 3. If the tree is empty, search is not possible 4. Otherwise, first search the root of the tree. 5. If the key does not match with the value in the root, search its subtrees. 6. If the value of the key is less than the root value, search the left subtree 7. If the value of the key is greater than the root value, search the right subtree. 8. If the key is not found in the tree, return unsuccessful search. 9. END
Example
Following are the implementations of this operation in various programming languages −
#include <stdio.h>
#include <stdlib.h>
struct node {
int data;
struct node *leftChild, *rightChild;
};
struct node *root = NULL;
struct node *newNode(int item){
struct node *temp = (struct node *)malloc(sizeof(struct node));
temp->data = item;
temp->leftChild = temp->rightChild = NULL;
return temp;
}
void insert(int data){
struct node *tempNode = (struct node*) malloc(sizeof(struct node));
struct node *current;
struct node *parent;
tempNode->data = data;
tempNode->leftChild = NULL;
tempNode->rightChild = NULL;
//if tree is empty
if(root == NULL) {
root = tempNode;
} else {
current = root;
parent = NULL;
while(1) {
parent = current;
//go to left of the tree
if(data < parent->data) {
current = current->leftChild;
//insert to the left
if(current == NULL) {
parent->leftChild = tempNode;
return;
}
}//go to right of the tree
else {
current = current->rightChild;
//insert to the right
if(current == NULL) {
parent->rightChild = tempNode;
return;
}
}
}
}
}
struct node* search(int data){
struct node *current = root;
while(current->data != data) {
//go to left tree
if(current->data > data) {
current = current->leftChild;
}//else go to right tree
else {
current = current->rightChild;
}
//not found
if(current == NULL) {
return NULL;
}
}
return current;
}
void printTree(struct node* Node){
if(Node == NULL)
return;
printTree(Node->leftChild);
printf(" --%d", Node->data);
printTree(Node->rightChild);
}
int main(){
insert(55);
insert(20);
insert(90);
insert(50);
insert(35);
insert(15);
insert(65);
printf("Insertion done");
printf("\nBST: \n");
printTree(root);
struct node* k;
int ele = 35;
printf("\nElement to be searched: %d", ele);
k = search(35);
if(k != NULL)
printf("\nElement %d found", k->data);
else
printf("\nElement not found");
return 0;
}
Output
Insertion done BST: --15 --20 --35 --50 --55 --65 --90 Element to be searched: 35 Element 35 found
#include <iostream>
using namespace std;
struct Node {
int data;
struct Node *leftChild, *rightChild;
};
Node *root = NULL;
Node *newNode(int item){
Node *temp = (Node *)malloc(sizeof(Node));
temp->data = item;
temp->leftChild = temp->rightChild = NULL;
return temp;
}
void insert(int data){
Node *tempNode = (Node*) malloc(sizeof(Node));
Node *current;
Node *parent;
tempNode->data = data;
tempNode->leftChild = NULL;
tempNode->rightChild = NULL;
//if tree is empty
if(root == NULL) {
root = tempNode;
} else {
current = root;
parent = NULL;
while(1) {
parent = current;
//go to left of the tree
if(data < parent->data) {
current = current->leftChild;
//insert to the left
if(current == NULL) {
parent->leftChild = tempNode;
return;
}
}//go to right of the tree
else {
current = current->rightChild;
//insert to the right
if(current == NULL) {
parent->rightChild = tempNode;
return;
}
}
}
}
}
Node* search(int data){
Node *current = root;
while(current->data != data) {
//go to left tree
if(current->data > data) {
current = current->leftChild;
}//else go to right tree
else {
current = current->rightChild;
}
//not found
if(current == NULL) {
return NULL;
}
}
return current;
}
void printTree(Node* Node) {
if (Node == nullptr)
return;
printTree(Node->leftChild);
cout << " --" << Node->data;
printTree(Node->rightChild);
}
int main(){
insert(55);
insert(20);
insert(90);
insert(50);
insert(35);
insert(15);
insert(65);
cout<<"Insertion done";
cout<<"\nBST: "<<endl;
printTree(root);
struct node* k;
int ele = 35;
cout<<"\nElement to be searched: "<<ele;
Node* result = search(35);
if(k != NULL)
cout<<"\nElement "<<result->data<<" found ";
else
cout<<"\nElement not found";
return 0;
}
Output
Insertion done BST: --15 --20 --35 --50 --55 --65 --90 Element to be searched: 35 Element 35 found
import java.util.Scanner;
class BSTNode {
BSTNode left, right;
int data;
public BSTNode(int n) {
left = null;
right = null;
data = n;
}
}
public class BST {
static BSTNode root;
public BST() {
root = null;
}
private BSTNode insert(BSTNode node, int data) {
if(node == null)
node = new BSTNode(data);
else {
if(data <= node.data)
node.left = insert(node.left, data);
else
node.right = insert(node.right, data);
}
return node;
}
private boolean search(BSTNode r, int val) {
boolean found = false;
while ((r != null) && !found) {
int rval = r.data;
if(val < rval)
r = r.left;
else if (val > rval)
r = r.right;
else {
found = true;
break;
}
found = search(r, val);
}
return found;
}
void printTree(BSTNode node, String prefix) {
if(node == null)
return;
printTree(node.left , " " + prefix);
System.out.print(prefix + "--" + node.data + " ");
printTree(node.right , prefix);
}
public static void main(String args[]) {
Scanner sc = new Scanner(System.in);
BST bst = new BST();
root = bst.insert(root, 55);
root = bst.insert(root, 20);
root = bst.insert(root, 90);
root = bst.insert(root, 80);
root = bst.insert(root, 50);
root = bst.insert(root, 35);
root = bst.insert(root, 15);
root = bst.insert(root, 65);
System.out.print("Insertion Done");
System.out.print("\nBST:\n");
bst.printTree(root, "");
int ele = 80;
System.out.print("\nElement to be searched: " + ele);
System.out.println("\nElement found: " + bst.search(root, 80));
}
}
Output
Insertion Done BST: --15 --20 --35 --50 --55 --65 --80 --90 Element to be searched: 80 Element found: true
class Node:
def __init__(self, data):
self.left = None
self.right = None
self.data = data
# Insert method to create nodes
def insert(self, data):
if self.data:
if data < self.data:
if self.left is None:
self.left = Node(data)
else:
self.left.insert(data)
elif data > self.data:
if self.right is None:
self.right = Node(data)
else:
self.right.insert(data)
else:
self.data = data
# search method to compare the value with nodes
def search(self, key):
if key < self.data:
if self.left is None:
return str(key)+" Not Found"
return self.left.search(key)
elif key > self.data:
if self.right is None:
return str(key)+" Not Found"
return self.right.search(key)
else:
print(str(self.data) + ' is found')
root = Node(54)
root.insert(34)
root.insert(46)
root.insert(12)
root.insert(23)
root.insert(5)
print(root.search(17))
print(root.search(12))
Output
17 Not Found 12 is found None
Insertion Operation
Whenever an element is to be inserted, first locate its proper location. Start searching from the root node, then if the data is less than the key value, search for the empty location in the left subtree and insert the data. Otherwise, search for the empty location in the right subtree and insert the data.
Algorithm
1. START 2. If the tree is empty, insert the first element as the root node of the tree. The following elements are added as the leaf nodes. 3. If an element is less than the root value, it is added into the left subtree as a leaf node. 4. If an element is greater than the root value, it is added into the right subtree as a leaf node. 5. The final leaf nodes of the tree point to NULL values as their child nodes. 6. END
Example
Following are the implementations of this operation in various programming languages −
#include <stdio.h>
#include <stdlib.h>
struct node {
int data;
struct node *leftChild, *rightChild;
};
struct node *root = NULL;
struct node *newNode(int item){
struct node *temp = (struct node *)malloc(sizeof(struct node));
temp->data = item;
temp->leftChild = temp->rightChild = NULL;
return temp;
}
void insert(int data){
struct node *tempNode = (struct node*) malloc(sizeof(struct node));
struct node *current;
struct node *parent;
tempNode->data = data;
tempNode->leftChild = NULL;
tempNode->rightChild = NULL;
//if tree is empty
if(root == NULL) {
root = tempNode;
} else {
current = root;
parent = NULL;
while(1) {
parent = current;
//go to left of the tree
if(data < parent->data) {
current = current->leftChild;
//insert to the left
if(current == NULL) {
parent->leftChild = tempNode;
return;
}
}//go to right of the tree
else {
current = current->rightChild;
//insert to the right
if(current == NULL) {
parent->rightChild = tempNode;
return;
}
}
}
}
}
void printTree(struct node* Node){
if(Node == NULL)
return;
printTree(Node->leftChild);
printf(" --%d", Node->data);
printTree(Node->rightChild);
}
int main(){
insert(55);
insert(20);
insert(90);
insert(50);
insert(35);
insert(15);
insert(65);
printf("Insertion done\n");
printf("BST: \n");
printTree(root);
return 0;
}
Output
Insertion done BST: --15 --20 --35 --50 --55 --65 --90
#include <iostream>
using namespace std;
struct node {
int data;
struct node *leftChild, *rightChild;
};
struct node *root = NULL;
struct node *newNode(int item){
struct node *temp = (struct node *)malloc(sizeof(struct node));
temp->data = item;
temp->leftChild = temp->rightChild = NULL;
return temp;
}
void insert(int data){
struct node *tempNode = (struct node*) malloc(sizeof(struct node));
struct node *current;
struct node *parent;
tempNode->data = data;
tempNode->leftChild = NULL;
tempNode->rightChild = NULL;
//if tree is empty
if(root == NULL) {
root = tempNode;
} else {
current = root;
parent = NULL;
while(1) {
parent = current;
//go to left of the tree
if(data < parent->data) {
current = current->leftChild;
//insert to the left
if(current == NULL) {
parent->leftChild = tempNode;
return;
}
}//go to right of the tree
else {
current = current->rightChild;
//insert to the right
if(current == NULL) {
parent->rightChild = tempNode;
return;
}
}
}
}
}
void printTree(struct node* Node){
if(Node == NULL)
return;
printTree(Node->leftChild);
cout<<" --"<<Node->data;
printTree(Node->rightChild);
}
int main(){
insert(55);
insert(20);
insert(90);
insert(50);
insert(35);
insert(15);
insert(65);
cout<<"Insertion done\n";
cout<<"BST:"<<endl;
printTree(root);
return 0;
}
Output
Insertion done BST: --15 --20 --35 --50 --55 --65 --90
import java.util.Scanner;
class BSTNode {
BSTNode left, right;
int data;
public BSTNode(int n) {
left = null;
right = null;
data = n;
}
}
public class BST {
static BSTNode root;
public BST() {
root = null;
}
private BSTNode insert(BSTNode node, int data) {
if(node == null)
node = new BSTNode(data);
else {
if(data <= node.data)
node.left = insert(node.left, data);
else
node.right = insert(node.right, data);
}
return node;
}
void printTree(BSTNode node, String prefix) {
if(node == null)
return;
printTree(node.left , " " + prefix);
System.out.print(prefix + "--" + node.data);
printTree(node.right , prefix + " ");
}
public static void main(String args[]) {
Scanner sc = new Scanner(System.in);
BST bst = new BST();
root = bst.insert(root, 55);
root = bst.insert(root, 20);
root = bst.insert(root, 90);
root = bst.insert(root, 80);
root = bst.insert(root, 50);
root = bst.insert(root, 35);
root = bst.insert(root, 15);
root = bst.insert(root, 65);
System.out.print("Insertion done\n");
System.out.print("BST:\n");
bst.printTree(root, " ");
}
}
Output
Insertion done BST: --15 --20 --35 --50 --55 --65 --80 --90
class Node:
def __init__(self, data):
self.left = None
self.right = None
self.data = data
# Insert method to create nodes
def insert(self, data):
if self.data:
if data self.data:
if self.right is None:
self.right = Node(data)
else:
self.right.insert(data)
else:
self.data = data
def printTree(self, prefex):
if self is None:
return
self.left.printTree(prefex + "") if self.left else None
print(prefex + "--", str(self.data),"", end = "")
self.right.printTree(prefex + "") if self.right else None
root = Node(54)
root.insert(34)
root.insert(46)
root.insert(12)
root.insert(23)
root.insert(5)
print("Insertion Done")
print("BST: ")
root.printTree('')
Output
Insertion Done BST: -- 5 -- 12 -- 23 -- 34 -- 46 -- 54
Inorder Traversal
The inorder traversal operation in a Binary Search Tree visits all its nodes in the following order −
Firstly, we traverse the left child of the root node/current node, if any.
Next, traverse the current node.
Lastly, traverse the right child of the current node, if any.
Algorithm
1. START 2. Traverse the left subtree, recursively 3. Then, traverse the root node 4. Traverse the right subtree, recursively. 5. END
Example
Following are the implementations of this operation in various programming languages −
#include <stdio.h>
#include <stdlib.h>
struct node {
int key;
struct node *left, *right;
};
struct node *newNode(int item){
struct node *temp = (struct node *)malloc(sizeof(struct node));
temp->key = item;
temp->left = temp->right = NULL;
return temp;
}
// Inorder Traversal
void inorder(struct node *root){
if (root != NULL) {
inorder(root->left);
printf("%d -> ", root->key);
inorder(root->right);
}
}
// Insertion operation
struct node *insert(struct node *node, int key){
if (node == NULL) return newNode(key);
if (key < node->key)
node->left = insert(node->left, key);
else
node->right = insert(node->right, key);
return node;
}
int main(){
struct node *root = NULL;
root = insert(root, 55);
root = insert(root, 20);
root = insert(root, 90);
root = insert(root, 50);
root = insert(root, 35);
root = insert(root, 15);
root = insert(root, 65);
printf("Inorder traversal: ");
inorder(root);
}
Output
Inorder traversal: 15 -> 20 -> 35 -> 50 -> 55 -> 65 -> 90 ->
#include <iostream>
struct node {
int key;
struct node *left, *right;
};
struct node *newNode(int item){
struct node *temp = (struct node *)malloc(sizeof(struct node));
temp->key = item;
temp->left = temp->right = NULL;
return temp;
}
// Inorder Traversal
void inorder(struct node *root){
if (root != NULL) {
inorder(root->left);
printf("%d -> ", root->key);
inorder(root->right);
}
}
// Insertion operation
struct node *insert(struct node *node, int key){
if (node == NULL) return newNode(key);
if (key < node->key)
node->left = insert(node->left, key);
else
node->right = insert(node->right, key);
return node;
}
int main(){
struct node *root = NULL;
root = insert(root, 55);
root = insert(root, 20);
root = insert(root, 90);
root = insert(root, 50);
root = insert(root, 35);
root = insert(root, 15);
root = insert(root, 65);
printf("Inorder traversal: ");
inorder(root);
}
Output
Inorder traversal: 15 -> 20 -> 35 -> 50 -> 55 -> 65 -> 90 ->
class Node {
int data;
Node leftChild;
Node rightChild;
public Node(int key) {
data = key;
leftChild = rightChild = null;
}
}
public class TreeDataStructure {
Node root = null;
void inorder_traversal(Node node) {
if(node != null) {
inorder_traversal(node.leftChild);
System.out.print(node.data + " ->");
inorder_traversal(node.rightChild);
}
}
public static void main(String args[]) {
TreeDataStructure tree = new TreeDataStructure();
tree.root = new Node(27);
tree.root.leftChild = new Node(12);
tree.root.rightChild = new Node(30);
tree.root.leftChild.leftChild = new Node(4);
tree.root.leftChild.rightChild = new Node(17);
tree.root.rightChild.leftChild = new Node(56);
System.out.println("Inorder traversal: ");
tree.inorder_traversal(tree.root);
}
}
Output
Inorder traversal: 4 ->12 ->17 ->27 ->56 ->30 ->
class Node:
def __init__(self, data):
self.left = None
self.right = None
self.data = data
# Insert method to create nodes
def insert(self, data):
if self.data:
if data < self.data:
if self.left is None:
self.left = Node(data)
else:
self.left.insert(data)
elif data > self.data:
if self.right is None:
self.right = Node(data)
else:
self.right.insert(data)
else:
self.data = data
# Print the tree
def Inorder(self):
if self.left:
self.left.Inorder()
print(self.data, "->", end = " ")
if self.right:
self.right.Inorder()
root = Node(54)
root.insert(34)
root.insert(46)
root.insert(12)
root.insert(23)
root.insert(5)
print("Inorder Traversal: ")
root.Inorder()
Output
Inorder Traversal: 12 -> 34 -> 54 ->
Preorder Traversal
The preorder traversal operation in a Binary Search Tree visits all its nodes. However, the root node in it is first printed, followed by its left subtree and then its right subtree.
Algorithm
1. START 2. Traverse the root node first. 3. Then traverse the left subtree, recursively 4. Later, traverse the right subtree, recursively. 5. END
Example
Following are the implementations of this operation in various programming languages −
#include <stdio.h>
#include <stdlib.h>
struct node {
int key;
struct node *left, *right;
};
struct node *newNode(int item){
struct node *temp = (struct node *)malloc(sizeof(struct node));
temp->key = item;
temp->left = temp->right = NULL;
return temp;
}
// Preorder Traversal
void preorder(struct node *root){
if (root != NULL) {
printf("%d -> ", root->key);
preorder(root->left);
preorder(root->right);
}
}
// Insertion operation
struct node *insert(struct node *node, int key){
if (node == NULL) return newNode(key);
if (key < node->key)
node->left = insert(node->left, key);
else
node->right = insert(node->right, key);
return node;
}
int main(){
struct node *root = NULL;
root = insert(root, 55);
root = insert(root, 20);
root = insert(root, 90);
root = insert(root, 50);
root = insert(root, 35);
root = insert(root, 15);
root = insert(root, 65);
printf("Preorder traversal: ");
preorder(root);
}
Output
Preorder traversal: 55 -> 20 -> 15 -> 50 -> 35 -> 90 -> 65 ->
#include <iostream>
struct node {
int key;
struct node *left, *right;
};
struct node *newNode(int item){
struct node *temp = (struct node *)malloc(sizeof(struct node));
temp->key = item;
temp->left = temp->right = NULL;
return temp;
}
// Preorder Traversal
void preorder(struct node *root){
if (root != NULL) {
printf("%d -> ", root->key);
preorder(root->left);
preorder(root->right);
}
}
// Insertion operation
struct node *insert(struct node *node, int key){
if (node == NULL) return newNode(key);
if (key < node->key)
node->left = insert(node->left, key);
else
node->right = insert(node->right, key);
return node;
}
int main(){
struct node *root = NULL;
root = insert(root, 55);
root = insert(root, 20);
root = insert(root, 90);
root = insert(root, 50);
root = insert(root, 35);
root = insert(root, 15);
root = insert(root, 65);
printf("Preorder traversal: ");
preorder(root);
}
Output
Preorder traversal: 55 -> 20 -> 15 -> 50 -> 35 -> 90 -> 65 ->
class Node {
int data;
Node leftChild;
Node rightChild;
public Node(int key) {
data = key;
leftChild = rightChild = null;
}
}
public class TreeDataStructure {
Node root = null;
void preorder_traversal(Node node) {
if(node != null) {
System.out.print(node.data + " ->");
preorder_traversal(node.leftChild);
preorder_traversal(node.rightChild);
}
}
public static void main(String args[]) {
TreeDataStructure tree = new TreeDataStructure();
tree.root = new Node(27);
tree.root.leftChild = new Node(12);
tree.root.rightChild = new Node(30);
tree.root.leftChild.leftChild = new Node(4);
tree.root.leftChild.rightChild = new Node(17);
tree.root.rightChild.leftChild = new Node(56);
System.out.println("Preorder traversal: ");
tree.preorder_traversal(tree.root);
}
}
Output
Preorder traversal: 27 ->12 ->4 ->17 ->30 ->56 ->
class Node:
def __init__(self, data):
self.left = None
self.right = None
self.data = data
# Insert method to create nodes
def insert(self, data):
if self.data:
if data < self.data:
if self.left is None:
self.left = Node(data)
else:
self.left.insert(data)
elif data > self.data:
if self.right is None:
self.right = Node(data)
else:
self.right.insert(data)
else:
self.data = data
# Print the tree
def Preorder(self):
print(self.data, "->", end = "")
if self.left:
self.left.Preorder()
if self.right:
self.right.Preorder()
root = Node(54)
root.insert(34)
root.insert(46)
root.insert(12)
root.insert(23)
root.insert(5)
print("Preorder Traversal: ")
root.Preorder()
Output
Preorder Traversal: 54 ->34 ->12 ->5 ->23 ->46 ->
Postorder Traversal
Like the other traversals, postorder traversal also visits all the nodes in a Binary Search Tree and displays them. However, the left subtree is printed first, followed by the right subtree and lastly, the root node.
Algorithm
1. START 2. Traverse the left subtree, recursively 3. Traverse the right subtree, recursively. 4. Then, traverse the root node 5. END
Example
Following are the implementations of this operation in various programming languages −
#include <stdio.h>
#include <stdlib.h>
struct node {
int key;
struct node *left, *right;
};
struct node *newNode(int item){
struct node *temp = (struct node *)malloc(sizeof(struct node));
temp->key = item;
temp->left = temp->right = NULL;
return temp;
}
// Postorder Traversal
void postorder(struct node *root){
if (root != NULL) {
printf("%d -> ", root->key);
postorder(root->left);
postorder(root->right);
}
}
// Insertion operation
struct node *insert(struct node *node, int key){
if (node == NULL) return newNode(key);
if (key < node->key)
node->left = insert(node->left, key);
else
node->right = insert(node->right, key);
return node;
}
int main(){
struct node *root = NULL;
root = insert(root, 55);
root = insert(root, 20);
root = insert(root, 90);
root = insert(root, 50);
root = insert(root, 35);
root = insert(root, 15);
root = insert(root, 65);
printf("Postorder traversal: ");
postorder(root);
}
Output
Postorder traversal: 55 -> 20 -> 15 -> 50 -> 35 -> 90 > 65 ->
#include <iostream>
struct node {
int key;
struct node *left, *right;
};
struct node *newNode(int item){
struct node *temp = (struct node *)malloc(sizeof(struct node));
temp->key = item;
temp->left = temp->right = NULL;
return temp;
}
// Postorder Traversal
void postorder(struct node *root){
if (root != NULL) {
printf("%d -> ", root->key);
postorder(root->left);
postorder(root->right);
}
}
// Insertion operation
struct node *insert(struct node *node, int key){
if (node == NULL) return newNode(key);
if (key < node->key)
node->left = insert(node->left, key);
else
node->right = insert(node->right, key);
return node;
}
int main(){
struct node *root = NULL;
root = insert(root, 55);
root = insert(root, 20);
root = insert(root, 90);
root = insert(root, 50);
root = insert(root, 35);
root = insert(root, 15);
root = insert(root, 65);
printf("Postorder traversal: ");
postorder(root);
}
Output
Postorder traversal: 55 -> 20 -> 15 -> 50 -> 35 -> 90 -> 65 ->
class Node {
int data;
Node leftChild;
Node rightChild;
public Node(int key) {
data = key;
leftChild = rightChild = null;
}
}
public class TreeDataStructure {
Node root = null;
void postorder_traversal(Node node) {
if(node != null) {
postorder_traversal(node.leftChild);
postorder_traversal(node.rightChild);
System.out.print(node.data + " ->");
}
}
public static void main(String args[]) {
TreeDataStructure tree = new TreeDataStructure();
tree.root = new Node(27);
tree.root.leftChild = new Node(12);
tree.root.rightChild = new Node(30);
tree.root.leftChild.leftChild = new Node(4);
tree.root.leftChild.rightChild = new Node(17);
tree.root.rightChild.leftChild = new Node(56);
System.out.println("Postorder traversal: ");
tree.postorder_traversal(tree.root);
}
}
Output
Postorder traversal: 4 ->17 ->12 ->56 ->30 ->27 ->
class Node:
def __init__(self, data):
self.left = None
self.right = None
self.data = data
# Insert method to create nodes
def insert(self, data):
if self.data:
if data < self.data:
if self.left is None:
self.left = Node(data)
else:
self.left.insert(data)
elif data > self.data:
if self.right is None:
self.right = Node(data)
else:
self.right.insert(data)
else:
self.data = data
# Print the tree
def Postorder(self):
if self.left:
self.left.Postorder()
if self.right:
self.right.Postorder()
print(self.data, "->", end = "")
root = Node(54)
root.insert(34)
root.insert(46)
root.insert(12)
root.insert(23)
root.insert(5)
print("Postorder Traversal: ")
root.Postorder()
Output
Postorder Traversal: 5 ->23 ->12 ->46 ->34 ->54 ->
Complete implementation
Following are the complete implementations of Binary Search Tree in various programming languages −
#include <stdio.h>
#include <stdlib.h>
struct node {
int data;
struct node *leftChild, *rightChild;
};
struct node *root = NULL;
struct node *newNode(int item){
struct node *temp = (struct node *)malloc(sizeof(struct node));
temp->data = item;
temp->leftChild = temp->rightChild = NULL;
return temp;
}
void insert(int data){
struct node *tempNode = (struct node*) malloc(sizeof(struct node));
struct node *current;
struct node *parent;
tempNode->data = data;
tempNode->leftChild = NULL;
tempNode->rightChild = NULL;
//if tree is empty
if(root == NULL) {
root = tempNode;
} else {
current = root;
parent = NULL;
while(1) {
parent = current;
//go to left of the tree
if(data < parent->data) {
current = current->leftChild;
//insert to the left
if(current == NULL) {
parent->leftChild = tempNode;
return;
}
}//go to right of the tree
else {
current = current->rightChild;
//insert to the right
if(current == NULL) {
parent->rightChild = tempNode;
return;
}
}
}
}
}
struct node* search(int data){
struct node *current = root;
while(current->data != data) {
if(current != NULL) {
//go to left tree
if(current->data > data) {
current = current->leftChild;
}//else go to right tree
else {
current = current->rightChild;
}
//not found
if(current == NULL) {
return NULL;
}
}
}
return current;
}
// Inorder Traversal
void inorder(struct node *root){
if (root != NULL) {
inorder(root->leftChild);
printf("%d -> ", root->data);
inorder(root->rightChild);
}
}
// Preorder Traversal
void preorder(struct node *root){
if (root != NULL) {
printf("%d -> ", root->data);
preorder(root->leftChild);
preorder(root->rightChild);
}
}
// Postorder Traversal
void postorder(struct node *root){
if (root != NULL) {
printf("%d -> ", root->data);
postorder(root->leftChild);
postorder(root->rightChild);
}
}
int main(){
insert(55);
insert(20);
insert(90);
insert(50);
insert(35);
insert(15);
insert(65);
printf("Insertion done");
printf("\nPreorder Traversal: ");
preorder(root);
printf("\nInorder Traversal: ");
inorder(root);
printf("\nPostorder Traversal: ");
postorder(root);
struct node* k;
int ele = 35;
printf("\nElement to be searched: %d", ele);
k = search(35);
if(k != NULL)
printf("\nElement %d found", k->data);
else
printf("\nElement not found");
return 0;
}
Output
Insertion done Preorder Traversal: 55 -> 20 -> 15 -> 50 -> 35 -> 90 -> 65 -> Inorder Traversal: 15 -> 20 -> 35 -> 50 -> 55 -> 65 -> 90 -> Postorder Traversal: 55 -> 20 -> 15 -> 50 -> 35 -> 90 -> 65 -> Element to be searched: 35 Element 35 found
#include <iostream>
using namespace std;
struct node {
int data;
struct node *leftChild, *rightChild;
};
struct node *root = NULL;
struct node *newNode(int item){
struct node *temp = (struct node *)malloc(sizeof(struct node));
temp->data = item;
temp->leftChild = temp->rightChild = NULL;
return temp;
}
void insert(int data){
struct node *tempNode = (struct node*) malloc(sizeof(struct node));
struct node *current;
struct node *parent;
tempNode->data = data;
tempNode->leftChild = NULL;
tempNode->rightChild = NULL;
//if tree is empty
if(root == NULL) {
root = tempNode;
} else {
current = root;
parent = NULL;
while(1) {
parent = current;
//go to left of the tree
if(data < parent->data) {
current = current->leftChild;
//insert to the left
if(current == NULL) {
parent->leftChild = tempNode;
return;
}
}//go to right of the tree
else {
current = current->rightChild;
//insert to the right
if(current == NULL) {
parent->rightChild = tempNode;
return;
}
}
}
}
}
struct node* search(int data){
struct node *current = root;
while(current->data != data) {
//go to left tree
if(current->data > data) {
current = current->leftChild;
}//else go to right tree
else {
current = current->rightChild;
}
//not found
if(current == NULL) {
return NULL;
}
}
return current;
}
// Inorder Traversal
void inorder(struct node *root){
if (root != NULL) {
inorder(root->leftChild);
cout<<root->data<<" ->";
inorder(root->rightChild);
}
}
// Preorder Traversala
void preorder(struct node *root){
if (root != NULL) {
cout<<root->data<<" ->";
preorder(root->leftChild);
preorder(root->rightChild);
}
}
// Postorder Traversal
void postorder(struct node *root){
if (root != NULL) {
cout<<" -> "<<root->data;
postorder(root->leftChild);
postorder(root->rightChild);
}
}
int main(){
insert(55);
insert(20);
insert(90);
insert(50);
insert(35);
insert(15);
insert(65);
cout<<"Insertion done ";
cout<<"\nPreorder Traversal: ";
preorder(root);
cout<<"\nInorder Traversal: ";
inorder(root);
cout<<"\nPostorder Traversal: ";
postorder(root);
struct node* k;
int ele = 35;
cout<<"\nElement tonbe searched: "<<ele;
k = search(35);
if(k != NULL)
cout<<"\nElement "<<k->data<<" found";
else
cout<<"\nElement not found";
return 0;
}
Output
Insertion done Preorder Traversal: 55 ->20 ->15 ->50 ->35 ->90 ->65 -> Inorder Traversal: 15 ->20 ->35 ->50 ->55 ->65 ->90 -> Postorder Traversal: -> 55 -> 20 -> 15 -> 50 -> 35 -> 90 -> 65 Element tonbe searched: 35 Element 35 found
import java.util.Scanner;
class BSTNode {
BSTNode left, right;
int data;
public BSTNode(int n) {
left = null;
right = null;
data = n;
}
}
public class BST {
static BSTNode root;
public BST() {
root = null;
}
public boolean isEmpty() {
return root == null;
}
private BSTNode insert(BSTNode node, int data) {
if(node == null)
node = new BSTNode(data);
else {
if(data <= node.data)
node.left = insert(node.left, data);
else
node.right = insert(node.right, data);
}
return node;
}
public void delete(int k) {
if(isEmpty ())
System.out.println("TREE EMPTY");
else if(search (k) == false)
System.out.println("SORRY " + k + " IS NOT PRESENT");
else {
root=delete(root,k);
System.out.println(k + " DELETED FROM THE TREE");
}
}
public BSTNode delete(BSTNode root, int k) {
BSTNode p, p2, n;
if(root.data == k) {
BSTNode lt, rt;
lt = root.left;
rt = root.right;
if(lt == null && rt == null) {
return null;
} else if(lt == null) {
p = rt;
return p;
} else if(rt == null) {
p = lt;
return p;
} else {
p2 = rt;
p = rt;
while(p.left != null)
p = p.left;
p.left = lt;
return p2;
}
}
if (k < root.data) {
n = delete(root.left, k);
root.left = n;
} else {
n = delete(root.right, k);
root.right = n;
}
return root;
}
public boolean search(int val) {
return search(root, val);
}
private boolean search(BSTNode r, int val) {
boolean found = false;
while ((r != null) && !found) {
int rval = r.data;
if(val < rval)
r = r.left;
else if (val > rval)
r = r.right;
else {
found = true;
break;
}
found = search(r, val);
}
return found;
}
void printTree(BSTNode node, String prefix) {
if(node == null)
return;
printTree(node.left , " " + prefix);
System.out.println(prefix + "--" + node.data);
printTree(node.right , prefix + " ");
}
public static void main(String args[]) {
Scanner sc = new Scanner(System.in);
BST bst = new BST();
root = bst.insert(root, 55);
root = bst.insert(root, 20);
root = bst.insert(root, 90);
root = bst.insert(root, 80);
root = bst.insert(root, 50);
root = bst.insert(root, 35);
root = bst.insert(root, 15);
root = bst.insert(root, 65);
bst.printTree(root, " ");
bst.delete(55);
System.out.println("Element found = " + bst.search(80));
System.out.println("Is Tree Empty? " + bst.isEmpty());
}
}
Output
--15
--20--35
--50
--55
--65
--80
--90
55 DELETED FROM THE TREE
Element found = true
Is Tree Empty? false
class Node:
def __init__(self, data):
self.left = None
self.right = None
self.data = data
# Insert method to create nodes
def insert(self, data):
if self.data:
if data < self.data:
if self.left is None:
self.left = Node(data)
else:
self.left.insert(data)
elif data > self.data:
if self.right is None:
self.right = Node(data)
else:
self.right.insert(data)
else:
self.data = data
# search method to compare the value with nodes
def search(self, key):
if key < self.data:
if self.left is None:
return str(key)+ " Not Found"
return self.left.search(key)
elif key > self.data:
if self.right is None:
return str(key)+" Not Found"
return self.right.search(key)
else:
print(str(self.data) + ' is found')
# Print the tree
def Inorder(self):
if self.left:
self.left.Inorder()
print(self.data , " ->", end = " ")
if self.right:
self.right.Inorder()
# Print the tree
def Preorder(self):
print(self.data, " ->", end = " ")
if self.left:
self.left.Preorder()
if self.right:
self.right.Preorder()
# Print the tree
def Postorder(self):
if self.left:
self.left.Postorder()
if self.right:
self.right.Postorder()
print(self.data, " ->", end = " ")
root = Node(54)
root.insert(34)
root.insert(46)
root.insert(12)
root.insert(23)
root.insert(5)
print("Insertion Done")
print("Preorder Traversal: ")
root.Preorder()
print("\nInorder Traversal: ")
root.Inorder()
print("\nPostorder Traversal: ")
root.Postorder()
ele = 17
print("\nElement to be searched: ", ele)
print(root.search(ele))
Output
Insertion Done Preorder Traversal: 54 -> 34 -> 12 -> 5 -> 23 -> 46 -> Inorder Traversal: 5 -> 12 -> 23 -> 34 -> 46 -> 54 -> Postorder Traversal: 5 -> 23 -> 12 -> 46 -> 34 -> 54 -> Element to be searched: 17 17 Not Found
