- Automata Theory - Applications
- Automata Terminology
- Basics of String in Automata
- Set Theory for Automata
- Finite Sets and Infinite Sets
- Algebraic Operations on Sets
- Relations Sets in Automata Theory
- Graph and Tree in Automata Theory
- Transition Table in Automata
- What is Queue Automata?
- Compound Finite Automata
- Complementation Process in DFA
- Closure Properties in Automata
- Concatenation Process in DFA
- Language and Grammars
- Language and Grammar
- Grammars in Theory of Computation
- Language Generated by a Grammar
- Chomsky Classification of Grammars
- Context-Sensitive Languages
- Finite Automata
- What is Finite Automata?
- Finite Automata Types
- Applications of Finite Automata
- Limitations of Finite Automata
- Two-way Deterministic Finite Automata
- Deterministic Finite Automaton (DFA)
- Non-deterministic Finite Automaton (NFA)
- NDFA to DFA Conversion
- Equivalence of NFA and DFA
- Dead State in Finite Automata
- Minimization of DFA
- Automata Moore Machine
- Automata Mealy Machine
- Moore vs Mealy Machines
- Moore to Mealy Machine
- Mealy to Moore Machine
- Myhill–Nerode Theorem
- Mealy Machine for 1’s Complement
- Finite Automata Exercises
- Complement of DFA
- Regular Expressions
- Regular Expression in Automata
- Regular Expression Identities
- Applications of Regular Expression
- Regular Expressions vs Regular Grammar
- Kleene Closure in Automata
- Arden’s Theorem in Automata
- Convert Regular Expression to Finite Automata
- Conversion of Regular Expression to DFA
- Equivalence of Two Finite Automata
- Equivalence of Two Regular Expressions
- Convert Regular Expression to Regular Grammar
- Convert Regular Grammar to Finite Automata
- Pumping Lemma in Theory of Computation
- Pumping Lemma for Regular Grammar
- Pumping Lemma for Regular Expression
- Pumping Lemma for Regular Languages
- Applications of Pumping Lemma
- Closure Properties of Regular Set
- Closure Properties of Regular Language
- Decision Problems for Regular Languages
- Decision Problems for Automata and Grammars
- Conversion of Epsilon-NFA to DFA
- Regular Sets in Theory of Computation
- Context-Free Grammars
- Context-Free Grammars (CFG)
- Derivation Tree
- Parse Tree
- Ambiguity in Context-Free Grammar
- CFG vs Regular Grammar
- Applications of Context-Free Grammar
- Left Recursion and Left Factoring
- Closure Properties of Context Free Languages
- Simplifying Context Free Grammars
- Removal of Useless Symbols in CFG
- Removal Unit Production in CFG
- Removal of Null Productions in CFG
- Linear Grammar
- Chomsky Normal Form (CNF)
- Greibach Normal Form (GNF)
- Pumping Lemma for Context-Free Grammars
- Decision Problems of CFG
- Pushdown Automata
- Pushdown Automata (PDA)
- Pushdown Automata Acceptance
- Deterministic Pushdown Automata
- Non-deterministic Pushdown Automata
- Construction of PDA from CFG
- CFG Equivalent to PDA Conversion
- Pushdown Automata Graphical Notation
- Pushdown Automata and Parsing
- Two-stack Pushdown Automata
- Turing Machines
- Basics of Turing Machine (TM)
- Representation of Turing Machine
- Examples of Turing Machine
- Turing Machine Accepted Languages
- Variations of Turing Machine
- Multi-tape Turing Machine
- Multi-head Turing Machine
- Multitrack Turing Machine
- Non-Deterministic Turing Machine
- Semi-Infinite Tape Turing Machine
- K-dimensional Turing Machine
- Enumerator Turing Machine
- Universal Turing Machine
- Restricted Turing Machine
- Convert Regular Expression to Turing Machine
- Two-stack PDA and Turing Machine
- Turing Machine as Integer Function
- Post–Turing Machine
- Turing Machine for Addition
- Turing Machine for Copying Data
- Turing Machine as Comparator
- Turing Machine for Multiplication
- Turing Machine for Subtraction
- Modifications to Standard Turing Machine
- Linear-Bounded Automata (LBA)
- Church's Thesis for Turing Machine
- Recursively Enumerable Language
- Computability & Undecidability
- Turing Language Decidability
- Undecidable Languages
- Turing Machine and Grammar
- Kuroda Normal Form
- Converting Grammar to Kuroda Normal Form
- Decidability
- Undecidability
- Reducibility
- Halting Problem
- Turing Machine Halting Problem
- Rice's Theorem in Theory of Computation
- Post’s Correspondence Problem (PCP)
- Types of Functions
- Recursive Functions
- Injective Functions
- Surjective Function
- Bijective Function
- Partial Recursive Function
- Total Recursive Function
- Primitive Recursive Function
- μ Recursive Function
- Ackermann’s Function
- Russell’s Paradox
- Gödel Numbering
- Recursive Enumerations
- Kleene's Theorem
- Kleene's Recursion Theorem
- Advanced Concepts
- Matrix Grammars
- Probabilistic Finite Automata
- Cellular Automata
- Reduction of CFG
- Reduction Theorem
- Regular expression to ∈-NFA
- Quotient Operation
- Parikh’s Theorem
- Ladner’s Theorem
Construction of an FA from an RE
We can use Thompson's Construction to find out a Finite Automaton from a Regular Expression. We will reduce the regular expression into smallest regular expressions and converting these to NFA and finally to DFA.
Some basic RA expressions are the following −
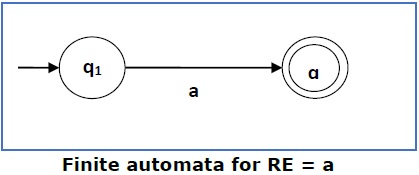
Case 1 − For a regular expression a, we can construct the following FA −
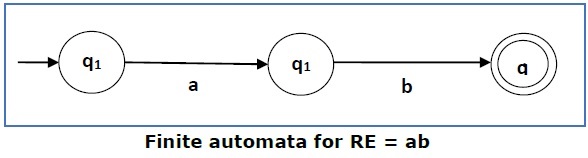
Case 2 − For a regular expression ab, we can construct the following FA −
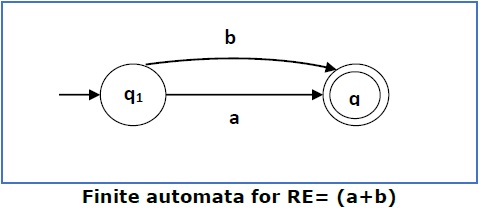
Case 3 − For a regular expression (a+b), we can construct the following FA −
Case 4 − For a regular expression (a+b)*, we can construct the following FA −
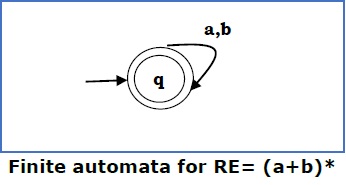
Method
Step 1 Construct an NFA with Null moves from the given regular expression.
Step 2 Remove Null transition from the NFA and convert it into its equivalent DFA.
Problem
Convert the following RA into its equivalent DFA − 1 (0 + 1)* 0
Solution
We will concatenate three expressions "1", "(0 + 1)*" and "0"
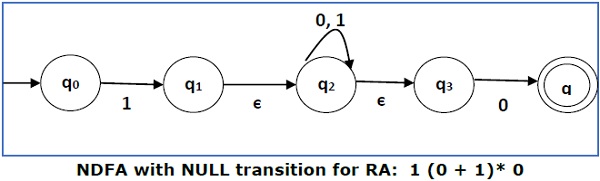
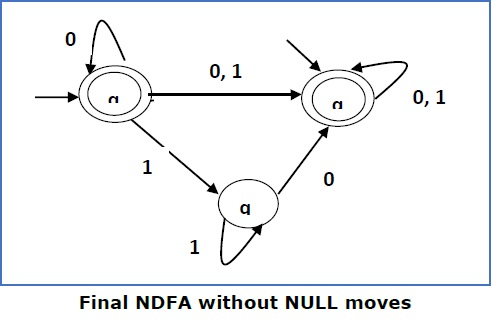
Now we will remove the ε transitions. After we remove the ε transitions from the NDFA, we get the following −
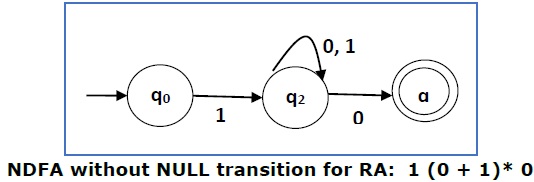
It is an NDFA corresponding to the RE − 1 (0 + 1)* 0. If you want to convert it into a DFA, simply apply the method of converting NDFA to DFA discussed in Chapter 1.
Finite Automata with Null Moves (NFA-ε)
A Finite Automaton with null moves (FA-ε) does transit not only after giving input from the alphabet set but also without any input symbol. This transition without input is called a null move.
An NFA-ε is represented formally by a 5-tuple (Q, ∑, δ, q0, F), consisting of
Q − a finite set of states
∑ − a finite set of input symbols
δ − a transition function : Q × (∑ ∪ {ε}) → 2Q
q0 − an initial state q0 ∈ Q
F − a set of final state/states of Q (F⊆Q).
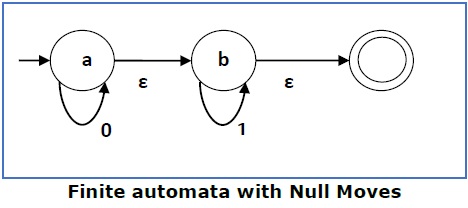
The above (FA-ε) accepts a string set − {0, 1, 01}
Removal of Null Moves from Finite Automata
If in an NDFA, there is -move between vertex X to vertex Y, we can remove it using the following steps −
- Find all the outgoing edges from Y.
- Copy all these edges starting from X without changing the edge labels.
- If X is an initial state, make Y also an initial state.
- If Y is a final state, make X also a final state.
Problem
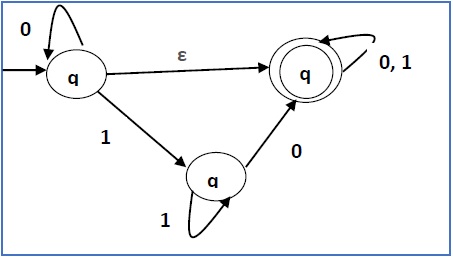
Convert the following NFA-ε to NFA without Null move.
Solution
Step 1 −
Here the ε transition is between q1 and q2, so let q1 is X and qf is Y.
Here the outgoing edges from qf is to qf for inputs 0 and 1.
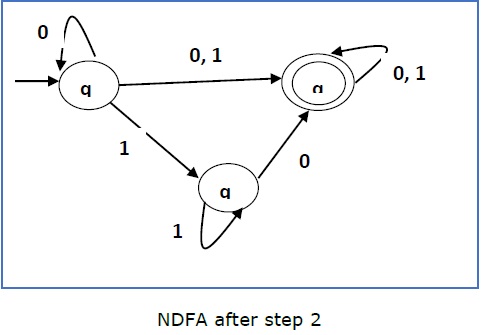
Step 2 −
Now we will Copy all these edges from q1 without changing the edges from qf and get the following FA −
Step 3 −
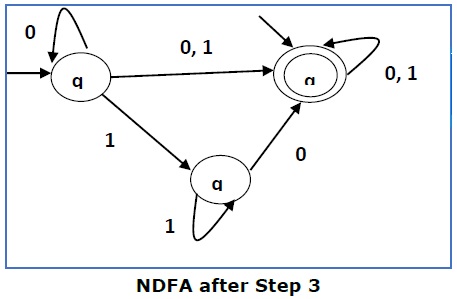
Here q1 is an initial state, so we make qf also an initial state.
So the FA becomes −
Step 4 −
Here qf is a final state, so we make q1 also a final state.
So the FA becomes −