Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
What is the conversion of a regular expression to finite Automata (NFA)?
A Regular Expression is a representation of Tokens. But, to recognize a token, it can need a token Recognizer, which is nothing but a Finite Automata (NFA). So, it can convert Regular Expression into NFA.
Algorithm for the conversion of Regular Expression to NFA
Input − A Regular Expression R
Output − NFA accepting language denoted by R
Method
For ε, NFA is
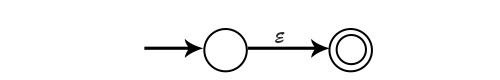
For a NFA is
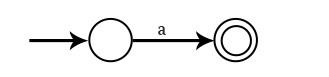
For a + b, or a | b NFA is
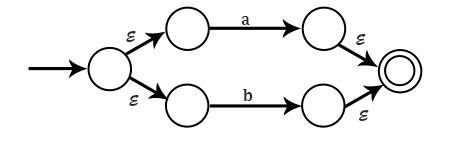
For ab, NFA is
For a*, NFA is
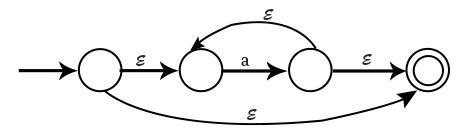
Example1 − Draw NFA for the Regular Expression a(a+b)*ab
Solution
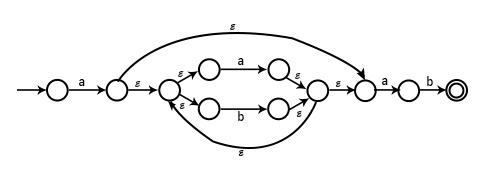
Example2 − Draw NFA for a + b + ab
Solution
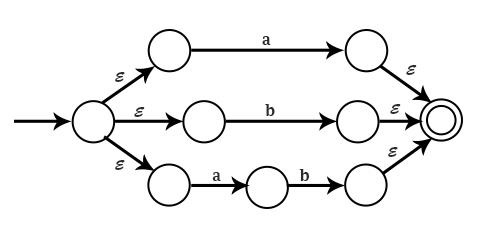
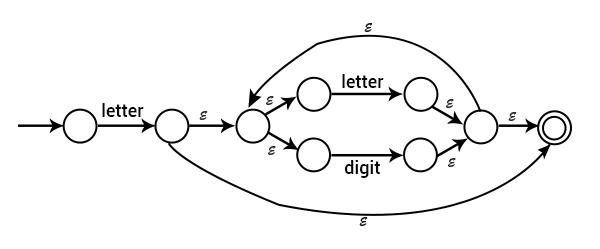
Example3 − Draw NFA for letter (letter+digit)*
Solution
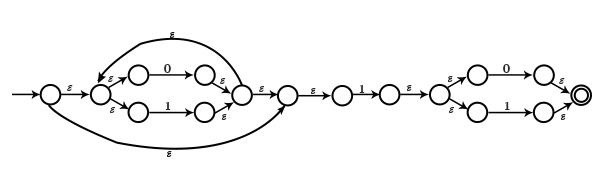
Example4 − Draw NFA corresponding to (0+1)*1(0+1)
Solution
ε−𝐜𝐥𝐨𝐬𝐮𝐫𝐞 (𝐬) − It is the set of states that can be reached form state s on ε−transitions alone.
- If s, t, u states. Initially, ε−closure (s)={s}.
- If s→t, then ε−closure (s)={s,t}.
- If s→t→u, then ε−closure (s)={s,t,u}
It will be repeated until all states are covered.
Algorithm: ε−𝐜𝐥𝐨𝐬𝐮𝐫𝐞 (𝐓)
T is a set of states whose ε−closure (s) is to be found.
Push All states in T on the stack
ε −closure (T)=T
While (stack not empty) {
Pop s, the top element of Stack
for each state t, with edge s→t {
if t is not present in ε−closure (T) {
ε−closure (T)=ε−closure (T)∪{t}
Push t on Stack
}
}
}Example − Find ε−closure(0),ε−closure(1),ε−closure(4)for following NFA.
Solution
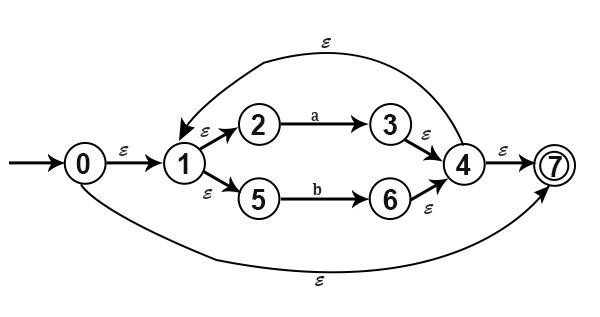
ε−closure(0)={0,1,2,5,7}
ε−closure(1)={1,2,5}
ε−closure(4)={4,7,1,2,5}
20K+ Views
