Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
How to generate regular expression from finite automata?
There are two methods for converting deterministic finite automata (DFA) to Regular expression (RE). These are as follows −
- Arden’s Method
- State Elimination Method
Let us understand these methods in detail.
Arden’s Theorem
Let P and Q be the two regular expressions.
If P does not contain null string, then following equation in R, viz R = Q + RP,
Which has a unique solution by R = QP*
Here,
The finite Automata do not have epsilon moves
It must have only initial state q1
It’s states are q1, q2, q3,…….qn. The final state may be some qi where i<=n
qi is the regular expression representing set of strings accepted by the finite automata even though qi is a final state
Using Arden's Theorem to find RE of DFA
To find the regular expression for the given automata, we first create equations of the given form for all the states as follows −
q1=q1α11+q2α21+----------+qnαn1+𝟄 q2=q1α12+q2α22+-----------+qnαn2 - - - - qn=q1α1n+q2α2n+------------+qnαnn.
By repeatedly applying substitutions and Arden’s Theorem we can express qi in terms of α ij’s . To get the set of strings recognized by FSA we have to take the union of all qi’s corresponding to final states.
Example
Note − For the parallel edges there will be many expressions for that state in the expression.
Then, we solve those equations to get the equation for qi in terms of α ij and that expression is the required solution, where qi is a final state.
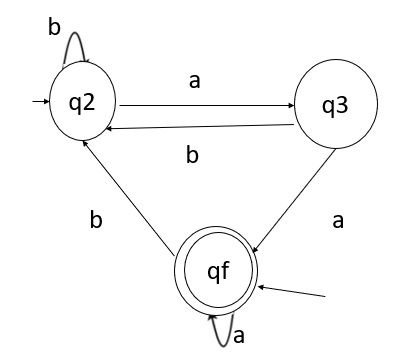
q 1= q a + q3a + € ( € move is because q1is the initial state)
q2 = q1b + q2b + q3b
q3 = q2a
Now, we will solve these three equations
- q2 = q1b + q2b + q3b
= q1b + q2b + (q2a)b (Substituting value of q3)
= q1b + q2(b + ab)
= q1b (b + ab) * (Applying Arden's Theorem)
- q1 = q1a + q3a + €
= q1a + q2aa + € (Substituting value of q3)
= q1a + q1b(b + ab*)aa + € (Substituting value of q2)
= q1(a + b(b + ab) *aa) + €
= € (a+ b(b + ab) *aa) *
= (a + b(b + ab) *aa) *
Hence, the regular expression is (a + b(b + ab) *aa) *.
State Elimination Method
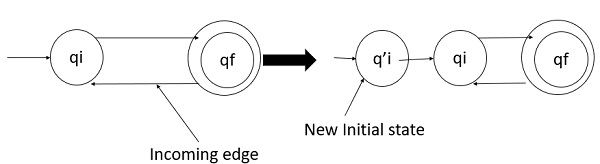
Step 1
Initial state of DFA does not have any incoming edge.
If there exists any incoming edge to the initial state, then we need to create a new initial state which has no incoming edge to it.
Example
Step 2
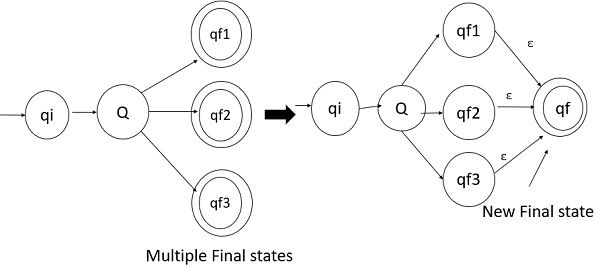
There must be only one final state in DFA.
If there exists multiple final states in DFA then we need to convert all final states into non-final states and create a new single final state.
Example
Step 3
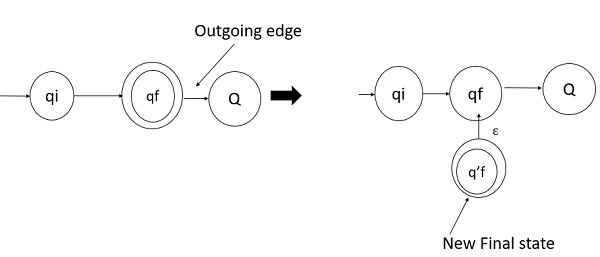
The final state of DFA does not have any outgoing edge.
If there exists any outgoing edge from the final state then, we need to create a new final state which has no outgoing edge from it.
Example
Step 4
Eliminate all intermediate states one after another. These states can be eliminated in any order
Finally, only an initial state going to the final state will be there.
The cost of this transition is required Regular Expression.
1K+ Views
