Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
What is Finite Automata in Compiler Design?
An automata is an abstract model of digital computers with discrete inputs and outputs. Every automata include a mechanism for reading inputs. It is considered that input is a string over a given alphabet, written on an input file that the automata can read. The input file is divided into smaller parts known as cells.
It is a Machine or a Recognizer for a language that is used to check whether a language accepts the string or not. In Finite Automata, Finite means a finite number of states and Automata means the Automatic Machine which works without any interference of human beings. A finite automata consist of a set of finite states and a set of transitions from state to state that appears on input symbols chosen from an alphabet $\sum$.
Representation of Finite Automata
There are two ways to represent finite Automata −
Transition Diagram
It is a directed graph or flow chart having states and edges.
Example
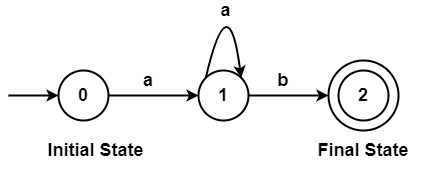
0, 1, 2→States 0 →Initial State 2→Final State a,b→Input Symbols
Transition Table
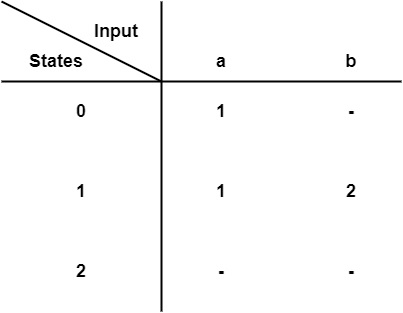
Finite Automata can be represented by 5 tuples (Q,∑,$\delta$,q0,F)
- Q is a finite non-empty set of states.
- $\sum$ is a finite set of input symbols.
- $\delta$ is the transition function.
- q0 ∈ Q is the initial state.
- F $\subseteq$ Q is the set of final states.
Example − Design Finite Automata which accepts string "abb".
Solution:
States: Q= {q0,q1,q2,q3}
Input Symbols: $\sum$ ={a,b}
Transition Function $\delta$: {$\delta$ (q0,𝑎)=q1,$\delta$(q1,𝑏)=q2,$\delta$(q2,b)=q3}
Initial State: q0
Final State (F) : {q3}
Types of Finite Automata
There are two types of finite automata which are as follows −
- Deterministic Finite Automata (DFA)
"Deterministic" means that on each input there is one and only one state to which the automata can have the transition from its current state.
DFA can be represented by 5 tuples (Q,$\sum$,$\delta$,q0,F)
- Q is a finite non-empty set of states.
- ∑ is a finite set of input symbols.
- $\delta$ is a transition function to move from the current state to the next state.
∴ $\delta$:Q x Σ → Q
- q0 ∈ Q is the initial state.
- F $\subseteq$ Q is the set of final states.
- Non-Deterministic Finite Automata (NFA)
"Non-Deterministic" means that there can be several possible transitions. So, the output is non-deterministic for a given input.
NFA can be represented by 5 tuples (Q,$\sum$,$\delta$,q0,F)
- Q is a finite non-empty set of states.
- ∑ is a finite set of input symbols.
- $\delta$ is the transition function to move from the current state to the next state.
∴ $\delta$:Q x $\sum$ → 2Q
- q0 ∈ Q is the initial state.
- F $\subseteq$ Q is the set of final states.
3K+ Views
