
- DSA - Home
- DSA - Overview
- DSA - Environment Setup
- DSA - Algorithms Basics
- DSA - Asymptotic Analysis
- Data Structures
- DSA - Data Structure Basics
- DSA - Data Structures and Types
- DSA - Array Data Structure
- DSA - Skip List Data Structure
- Linked Lists
- DSA - Linked List Data Structure
- DSA - Doubly Linked List Data Structure
- DSA - Circular Linked List Data Structure
- Stack & Queue
- DSA - Stack Data Structure
- DSA - Expression Parsing
- DSA - Queue Data Structure
- DSA - Circular Queue Data Structure
- DSA - Priority Queue Data Structure
- DSA - Deque Data Structure
- Searching Algorithms
- DSA - Searching Algorithms
- DSA - Linear Search Algorithm
- DSA - Binary Search Algorithm
- DSA - Interpolation Search
- DSA - Jump Search Algorithm
- DSA - Exponential Search
- DSA - Fibonacci Search
- DSA - Sublist Search
- DSA - Hash Table
- Sorting Algorithms
- DSA - Sorting Algorithms
- DSA - Bubble Sort Algorithm
- DSA - Insertion Sort Algorithm
- DSA - Selection Sort Algorithm
- DSA - Merge Sort Algorithm
- DSA - Shell Sort Algorithm
- DSA - Heap Sort Algorithm
- DSA - Bucket Sort Algorithm
- DSA - Counting Sort Algorithm
- DSA - Radix Sort Algorithm
- DSA - Quick Sort Algorithm
- Matrices Data Structure
- DSA - Matrices Data Structure
- DSA - Lup Decomposition In Matrices
- DSA - Lu Decomposition In Matrices
- Graph Data Structure
- DSA - Graph Data Structure
- DSA - Depth First Traversal
- DSA - Breadth First Traversal
- DSA - Spanning Tree
- DSA - Topological Sorting
- DSA - Strongly Connected Components
- DSA - Biconnected Components
- DSA - Augmenting Path
- DSA - Network Flow Problems
- DSA - Flow Networks In Data Structures
- DSA - Edmonds Blossom Algorithm
- DSA - Maxflow Mincut Theorem
- Tree Data Structure
- DSA - Tree Data Structure
- DSA - Tree Traversal
- DSA - Binary Search Tree
- DSA - AVL Tree
- DSA - Red Black Trees
- DSA - B Trees
- DSA - B+ Trees
- DSA - Splay Trees
- DSA - Range Queries
- DSA - Segment Trees
- DSA - Fenwick Tree
- DSA - Fusion Tree
- DSA - Hashed Array Tree
- DSA - K-Ary Tree
- DSA - Kd Trees
- DSA - Priority Search Tree Data Structure
- Recursion
- DSA - Recursion Algorithms
- DSA - Tower of Hanoi Using Recursion
- DSA - Fibonacci Series Using Recursion
- Divide and Conquer
- DSA - Divide and Conquer
- DSA - Max-Min Problem
- DSA - Strassen's Matrix Multiplication
- DSA - Karatsuba Algorithm
- Greedy Algorithms
- DSA - Greedy Algorithms
- DSA - Travelling Salesman Problem (Greedy Approach)
- DSA - Prim's Minimal Spanning Tree
- DSA - Kruskal's Minimal Spanning Tree
- DSA - Dijkstra's Shortest Path Algorithm
- DSA - Map Colouring Algorithm
- DSA - Fractional Knapsack Problem
- DSA - Job Sequencing with Deadline
- DSA - Optimal Merge Pattern Algorithm
- Dynamic Programming
- DSA - Dynamic Programming
- DSA - Matrix Chain Multiplication
- DSA - Floyd Warshall Algorithm
- DSA - 0-1 Knapsack Problem
- DSA - Longest Common Sub-sequence Algorithm
- DSA - Travelling Salesman Problem (Dynamic Approach)
- Hashing
- DSA - Hashing Data Structure
- DSA - Collision In Hashing
- Disjoint Set
- DSA - Disjoint Set
- DSA - Path Compression And Union By Rank
- Heap
- DSA - Heap Data Structure
- DSA - Binary Heap
- DSA - Binomial Heap
- DSA - Fibonacci Heap
- Tries Data Structure
- DSA - Tries
- DSA - Standard Tries
- DSA - Compressed Tries
- DSA - Suffix Tries
- Treaps
- DSA - Treaps Data Structure
- Bit Mask
- DSA - Bit Mask In Data Structures
- Bloom Filter
- DSA - Bloom Filter Data Structure
- Approximation Algorithms
- DSA - Approximation Algorithms
- DSA - Vertex Cover Algorithm
- DSA - Set Cover Problem
- DSA - Travelling Salesman Problem (Approximation Approach)
- Randomized Algorithms
- DSA - Randomized Algorithms
- DSA - Randomized Quick Sort Algorithm
- DSA - Karger’s Minimum Cut Algorithm
- DSA - Fisher-Yates Shuffle Algorithm
- Miscellaneous
- DSA - Infix to Postfix
- DSA - Bellmon Ford Shortest Path
- DSA - Maximum Bipartite Matching
- DSA Useful Resources
- DSA - Questions and Answers
- DSA - Selection Sort Interview Questions
- DSA - Merge Sort Interview Questions
- DSA - Insertion Sort Interview Questions
- DSA - Heap Sort Interview Questions
- DSA - Bubble Sort Interview Questions
- DSA - Bucket Sort Interview Questions
- DSA - Radix Sort Interview Questions
- DSA - Cycle Sort Interview Questions
- DSA - Quick Guide
- DSA - Useful Resources
- DSA - Discussion
Hamiltonian Cycle
What is a Hamiltonian Cycle?
A Hamiltonian Cycle or Circuit is a path in a graph that visits every vertex exactly once and returns to the starting vertex, forming a closed loop. A graph is said to be a Hamiltonian graph only when it contains a hamiltonian cycle, otherwise, it is called non-Hamiltonian graph.
A graph is an abstract data type (ADT) consisting of a set of objects that are connected via links.
The practical applications of hamiltonian cycle problem can be seen in the fields like network design, delivery systems and many more. However, the solution to this problem can be found only for small types of graphs, and not for larger ones.
Input Output Scenario
Suppose the given undirected graph G(V, E) and its adjacency matrix are as follows −
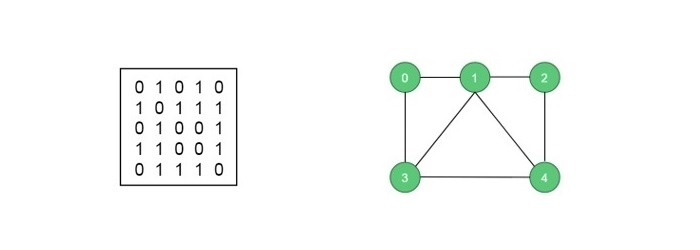
The backtracking algorithm can be used to find a Hamiltonian path in the above graph. If found, the algorithm returns the path. If not, it returns false. For this case, the output should be (0, 1, 2, 4, 3, 0).
Finding Hamiltonian Cycle using Backtracking Approach
The naive way to solve Hamiltonian cycle problem is by generating all possible configurations of vertices and checking if any configuration satisfies the given constraints. However, this approach is not suitable for large graphs as its time complexity will be (O(N!)).
The following steps explain the working of backtracking approach −
First, create an empty path array and add a starting vertex 0 to it.
Next, start with vertex 1 and then add other vertices one by one.
While adding vertices, check whether a given vertex is adjacent to the previously added vertex and hasn't been added already.
If any such vertex is found, add it to the path as part of the solution, otherwise, return false.
Example
The following example demonstrates how to find a hamiltonian cycle within a given undirected graph.
#include <stdio.h>
#define NODE 5
int graph[NODE][NODE] = {
{0, 1, 0, 1, 0},
{1, 0, 1, 1, 1},
{0, 1, 0, 0, 1},
{1, 1, 0, 0, 1},
{0, 1, 1, 1, 0},
};
int path[NODE];
// Function to display the Hamiltonian cycle
void displayCycle() {
printf("Cycle Found: ");
for (int i = 0; i < NODE; i++)
printf("%d ", path[i]);
// Print the first vertex again
printf("%d\n", path[0]);
}
// Function to check if adding vertex v to the path is valid
int isValid(int v, int k) {
// If there is no edge between path[k-1] and v
if (graph[path[k - 1]][v] == 0)
return 0;
// Check if vertex v is already taken in the path
for (int i = 0; i < k; i++)
if (path[i] == v)
return 0;
return 1;
}
// Function to find the Hamiltonian cycle
int cycleFound(int k) {
// When all vertices are in the path
if (k == NODE) {
// Check if there is an edge between the last and first vertex
if (graph[path[k - 1]][path[0]] == 1)
return 1;
else
return 0;
}
// Try adding each vertex (except the starting point) to the path
for (int v = 1; v < NODE; v++) {
if (isValid(v, k)) {
path[k] = v;
if (cycleFound(k + 1) == 1)
return 1;
// Backtrack: Remove v from the path
path[k] = -1;
}
}
return 0;
}
// Function to find and display the Hamiltonian cycle
int hamiltonianCycle() {
for (int i = 0; i < NODE; i++)
path[i] = -1;
// Set the first vertex as 0
path[0] = 0;
if (cycleFound(1) == 0) {
printf("Solution does not exist\n");
return 0;
}
displayCycle();
return 1;
}
int main() {
hamiltonianCycle();
return 0;
}
#include <iostream>
#define NODE 5
using namespace std;
int graph[NODE][NODE] = {
{0, 1, 0, 1, 0},
{1, 0, 1, 1, 1},
{0, 1, 0, 0, 1},
{1, 1, 0, 0, 1},
{0, 1, 1, 1, 0},
};
int path[NODE];
// Function to display the Hamiltonian cycle
void displayCycle() {
cout << "Cycle Found: ";
for (int i = 0; i < NODE; i++)
cout << path[i] << " ";
// Print the first vertex again
cout << path[0] << endl;
}
// Function to check if adding vertex v to the path is valid
bool isValid(int v, int k) {
// If there is no edge between path[k-1] and v
if (graph[path[k - 1]][v] == 0)
return false;
// Check if vertex v is already taken in the path
for (int i = 0; i < k; i++)
if (path[i] == v)
return false;
return true;
}
// function to find the Hamiltonian cycle
bool cycleFound(int k) {
// When all vertices are in the path
if (k == NODE) {
// Check if there is an edge between the last and first vertex
if (graph[path[k - 1]][path[0]] == 1)
return true;
else
return false;
}
// adding each vertex to the path
for (int v = 1; v < NODE; v++) {
if (isValid(v, k)) {
path[k] = v;
if (cycleFound(k + 1) == true)
return true;
// Remove v from the path
path[k] = -1;
}
}
return false;
}
// Function to find and display the Hamiltonian cycle
bool hamiltonianCycle() {
for (int i = 0; i < NODE; i++)
path[i] = -1;
// Set the first vertex as 0
path[0] = 0;
if (cycleFound(1) == false) {
cout << "Solution does not exist" << endl;
return false;
}
displayCycle();
return true;
}
int main() {
hamiltonianCycle();
}
public class HamiltonianCycle {
static final int NODE = 5;
static int[][] graph = {
{0, 1, 0, 1, 0},
{1, 0, 1, 1, 1},
{0, 1, 0, 0, 1},
{1, 1, 0, 0, 1},
{0, 1, 1, 1, 0}
};
static int[] path = new int[NODE];
// method to display the Hamiltonian cycle
static void displayCycle() {
System.out.print("Cycle Found: ");
for (int i = 0; i < NODE; i++)
System.out.print(path[i] + " ");
// Print the first vertex again
System.out.println(path[0]);
}
// method to check if adding vertex v to the path is valid
static boolean isValid(int v, int k) {
// If there is no edge between path[k-1] and v
if (graph[path[k - 1]][v] == 0)
return false;
// Check if vertex v is already taken in the path
for (int i = 0; i < k; i++)
if (path[i] == v)
return false;
return true;
}
// method to find the Hamiltonian cycle
static boolean cycleFound(int k) {
// When all vertices are in the path
if (k == NODE) {
// Check if there is an edge between the last and first vertex
if (graph[path[k - 1]][path[0]] == 1)
return true;
else
return false;
}
// adding each vertex (except the starting point) to the path
for (int v = 1; v < NODE; v++) {
if (isValid(v, k)) {
path[k] = v;
if (cycleFound(k + 1))
return true;
// Remove v from the path
path[k] = -1;
}
}
return false;
}
// method to find and display the Hamiltonian cycle
static boolean hamiltonianCycle() {
for (int i = 0; i < NODE; i++)
path[i] = -1;
// Set the first vertex as 0
path[0] = 0;
if (!cycleFound(1)) {
System.out.println("Solution does not exist");
return false;
}
displayCycle();
return true;
}
public static void main(String[] args) {
hamiltonianCycle();
}
}
NODE = 5
graph = [
[0, 1, 0, 1, 0],
[1, 0, 1, 1, 1],
[0, 1, 0, 0, 1],
[1, 1, 0, 0, 1],
[0, 1, 1, 1, 0]
]
path = [None] * NODE
# Function to display the Hamiltonian cycle
def displayCycle():
print("Cycle Found:", end=" ")
for i in range(NODE):
print(path[i], end=" ")
# Print the first vertex again
print(path[0])
# Function to check if adding vertex v to the path is valid
def isValid(v, k):
# If there is no edge between path[k-1] and v
if graph[path[k - 1]][v] == 0:
return False
# Check if vertex v is already taken in the path
for i in range(k):
if path[i] == v:
return False
return True
# Function to find the Hamiltonian cycle
def cycleFound(k):
# When all vertices are in the path
if k == NODE:
# Check if there is an edge between the last and first vertex
if graph[path[k - 1]][path[0]] == 1:
return True
else:
return False
# adding each vertex (except the starting point) to the path
for v in range(1, NODE):
if isValid(v, k):
path[k] = v
if cycleFound(k + 1):
return True
# Remove v from the path
path[k] = None
return False
# Function to find and display the Hamiltonian cycle
def hamiltonianCycle():
for i in range(NODE):
path[i] = None
# Set the first vertex as 0
path[0] = 0
if not cycleFound(1):
print("Solution does not exist")
return False
displayCycle()
return True
if __name__ == "__main__":
hamiltonianCycle()
Output
Cycle Found: 0 1 2 4 3 0