Sudoku Solving algorithms

What is a Sudoku?

Sudoku is a logical puzzle where a partially filled 9x9 grid needs to be filled with numbers from 1 to 9, ensuring that each row and column contains all digits from 1 to 9 uniquely. Also, each 3x3 sub-grid (also called a box) contains all digits from 1 to 9 uniquely. There are several algorithms that solve this puzzle efficiently. In this tutorial, we are going to learn how to solve a sudoku puzzle using backtracking.

Backtracking Approach to solve Sudoku

Suppose the given 9x9 matrix represents a sudoku grid. In it, the blank spaces are denoted by 0. The final output matrix (Sudoku grid) will be filled with numbers. If the solution does not exist, it will return false. The figure below illustrates the problem and solution of the given sudoku −

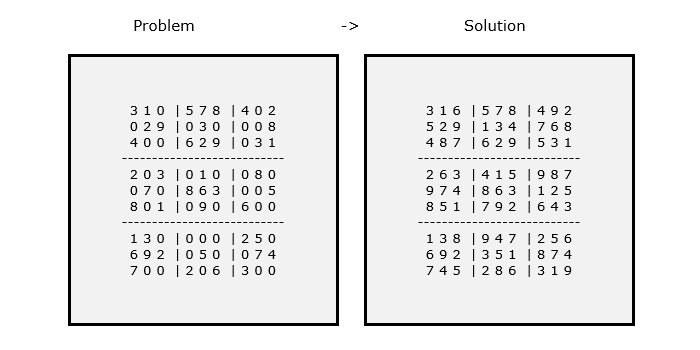
Sudoku Solving

In the naive method to solve sudoku problem, the algorithm generates all possible combinations of numbers from 1 to 9 to fill the empty cell. After assigning a number to each cell one by one, check whether the assignment is valid or not. This way of solving sudoku problems is very lengthy and time consuming.

Steps

Follow the below steps to solve sudoku problem using the backtracking approach −

  • First, identify empty cells which is defined by 0.

  • If an empty cell is found, check if it is valid to put a number in that cell by checking whether the number already exists in the same row, column, or 3x3 sub-grid.

  • If it is valid to place a number in the cell, the number is assigned to the cell. Otherwise, backtrack and assign 0 again.

Example

In this example, we are illustrating how to solve the Sudoku problem in various programming languages.

C C++ Java Python 
#include <stdio.h>
#define N 9
int grid[N][N] = { 
    { 3, 1, 0, 5, 7, 8, 4, 0, 2 },
    { 0, 2, 9, 0, 3, 0, 0, 0, 8 },
    { 4, 0, 0, 6, 2, 9, 0, 3, 1 },
    { 2, 0, 3, 0, 1, 0, 0, 8, 0 },
    { 0, 7, 0, 8, 6, 3, 0, 0, 5 },
    { 8, 0, 1, 0, 9, 0, 6, 0, 0 },
    { 1, 3, 0, 0, 0, 0, 2, 5, 0 },
    { 6, 9, 2, 0, 5, 0, 0, 7, 4 },
    { 7, 0, 0, 2, 0, 6, 3, 0, 0 }
};
//check whether num is present in col or not
int isPresentInCol(int col, int num) {    
   for (int row = 0; row < N; row++)
      if (grid[row][col] == num)
         return 1;
   return 0;
}
//check whether num is present in row or not
int isPresentInRow(int row, int num) {    
   for (int col = 0; col < N; col++)
      if (grid[row][col] == num)
         return 1;
   return 0;
}
//check whether num is present in 3x3 box or not
int isPresentInBox(int boxStartRow, int boxStartCol, int num) {    
   for (int row = 0; row < 3; row++)
      for (int col = 0; col < 3; col++)
         if (grid[row+boxStartRow][col+boxStartCol] == num)
            return 1;
   return 0;
}
//print the sudoku grid after solving
void sudokuGrid() {   
   for (int row = 0; row < N; row++) {
      for (int col = 0; col < N; col++) {
         if(col == 3 || col == 6)
            printf(" | ");
         printf("%d ", grid[row][col]);
      }
      if(row == 2 || row == 5) {
         printf("\n");
         for(int i = 0; i<N; i++)
            printf("---");
      }
      printf("\n");
   }
}
//get empty location and update row and column
int findEmptyPlace(int *row, int *col) {    
   for (*row = 0; *row < N; (*row)++)
      for (*col = 0; *col < N; (*col)++)
         //marked with 0 is empty
         if (grid[*row][*col] == 0) 
            return 1;
   return 0;
}
int isValidPlace(int row, int col, int num) {
   //when item not found in col, row and current 3x3 box
   return !isPresentInRow(row, num) && !isPresentInCol(col, num) && !isPresentInBox(row - row%3 , col - col%3, num);
}
int solveSudoku() {
   int row, col;
   //when all places are filled
   if (!findEmptyPlace(&row, &col))
      return 1;     
    //valid numbers are 1 - 9      
   for (int num = 1; num <= 9; num++) { 
      //check validation, if yes, put the number in the grid 
      if (isValidPlace(row, col, num)) {    
         grid[row][col] = num;
         //recursively go for other rooms in the grid
         if (solveSudoku())     
            return 1;
         //turn to unassigned space when conditions are not satisfied    
         grid[row][col] = 0;    
      }
   }
   return 0;
}
int main() {
   if (solveSudoku() == 1)
      sudokuGrid();
   else
      printf("Can't get a solution");
}

#include <iostream>
#define N 9
using namespace std;
int grid[N][N] = { 
    { 3, 1, 0, 5, 7, 8, 4, 0, 2 },
    { 0, 2, 9, 0, 3, 0, 0, 0, 8 },
    { 4, 0, 0, 6, 2, 9, 0, 3, 1 },
    { 2, 0, 3, 0, 1, 0, 0, 8, 0 },
    { 0, 7, 0, 8, 6, 3, 0, 0, 5 },
    { 8, 0, 1, 0, 9, 0, 6, 0, 0 },
    { 1, 3, 0, 0, 0, 0, 2, 5, 0 },
    { 6, 9, 2, 0, 5, 0, 0, 7, 4 },
    { 7, 0, 0, 2, 0, 6, 3, 0, 0 }
};
//check whether num is present in col or not
bool isPresentInCol(int col, int num) {    
   for (int row = 0; row < N; row++)
      if (grid[row][col] == num)
         return true;
   return false;
}
//check whether num is present in row or not
bool isPresentInRow(int row, int num) {    
   for (int col = 0; col < N; col++)
      if (grid[row][col] == num)
         return true;
   return false;
}
//check whether num is present in 3x3 box or not
bool isPresentInBox(int boxStartRow, int boxStartCol, int num) {    
   for (int row = 0; row < 3; row++)
      for (int col = 0; col < 3; col++)
         if (grid[row+boxStartRow][col+boxStartCol] == num)
            return true;
   return false;
}
 //print the sudoku grid after solving
void sudokuGrid() {   
   for (int row = 0; row < N; row++) {
      for (int col = 0; col < N; col++) {
         if(col == 3 || col == 6)
            cout << " | ";
         cout << grid[row][col] <<" ";
      }
      if(row == 2 || row == 5) {
         cout << endl;
         for(int i = 0; i<N; i++)
            cout << "---";
      }
      cout << endl;
   }
}
//get empty location and update row and column
bool findEmptyPlace(int &row, int &col) {    
   for (row = 0; row < N; row++)
      for (col = 0; col < N; col++)
         //marked with 0 is empty
         if (grid[row][col] == 0) 
            return true;
   return false;
}
bool isValidPlace(int row, int col, int num) {
   //when item not found in col, row and current 3x3 box
   return !isPresentInRow(row, num) && !isPresentInCol(col, num) && !isPresentInBox(row - row%3 , col - col%3, num);
}
bool solveSudoku() {
   int row, col;
   //when all places are filled
   if (!findEmptyPlace(row, col))
      return true;     
    //valid numbers are 1 - 9      
   for (int num = 1; num <= 9; num++) { 
      //check validation, if yes, put the number in the grid 
      if (isValidPlace(row, col, num)) {    
         grid[row][col] = num;
         //recursively go for other rooms in the grid
         if (solveSudoku())     
            return true;
         //turn to unassigned space when conditions are not satisfied    
         grid[row][col] = 0;    
      }
   }
   return false;
}
int main() {
   if (solveSudoku() == true)
      sudokuGrid();
   else
      cout << "Can't get a solution";
}

public class Main {
    static int N = 9;
    static int[][] grid = { 
        { 3, 1, 0, 5, 7, 8, 4, 0, 2 },
        { 0, 2, 9, 0, 3, 0, 0, 0, 8 },
        { 4, 0, 0, 6, 2, 9, 0, 3, 1 },
        { 2, 0, 3, 0, 1, 0, 0, 8, 0 },
        { 0, 7, 0, 8, 6, 3, 0, 0, 5 },
        { 8, 0, 1, 0, 9, 0, 6, 0, 0 },
        { 1, 3, 0, 0, 0, 0, 2, 5, 0 },
        { 6, 9, 2, 0, 5, 0, 0, 7, 4 },
        { 7, 0, 0, 2, 0, 6, 3, 0, 0 }
    };
    //check whether num is present in col or not
    static boolean isPresentInCol(int col, int num) {    
       for (int row = 0; row < N; row++)
          if (grid[row][col] == num)
             return true;
       return false;
    }
    //check whether num is present in row or not
    static boolean isPresentInRow(int row, int num) {    
       for (int col = 0; col < N; col++)
          if (grid[row][col] == num)
             return true;
       return false;
    }
    //check whether num is present in 3x3 box or not
    static boolean isPresentInBox(int boxStartRow, int boxStartCol, int num) {    
       for (int row = 0; row < 3; row++)
          for (int col = 0; col < 3; col++)
             if (grid[row+boxStartRow][col+boxStartCol] == num)
                return true;
       return false;
    }
    //print the sudoku grid after solving
    static void sudokuGrid() {   
       for (int row = 0; row < N; row++) {
          for (int col = 0; col < N; col++) {
             if(col == 3 || col == 6)
                System.out.print(" | ");
             System.out.print(grid[row][col] + " ");
          }
          if(row == 2 || row == 5) {
             System.out.println();
             for(int i = 0; i<N; i++)
                System.out.print("---");
          }
          System.out.println();
       }
    }
    //get empty location and update row and column
    static int[] findEmptyPlace() {    
       for (int row = 0; row < N; row++)
          for (int col = 0; col < N; col++)
             //marked with 0 is empty
             if (grid[row][col] == 0) 
                return new int[] {row, col};
       return null;
    }
    static boolean isValidPlace(int row, int col, int num) {
       //when item not found in col, row and current 3x3 box
       return !isPresentInRow(row, num) && !isPresentInCol(col, num) && !isPresentInBox(row - row%3 , col - col%3, num);
    }
    static boolean solveSudoku() {
       int row, col;
       int[] emptyPlace = findEmptyPlace();
       if (emptyPlace == null)
          return true;     
        //valid numbers are 1 - 9      
       for (int num = 1; num <= 9; num++) { 
          //check validation, if yes, put the number in the grid 
          if (isValidPlace(emptyPlace[0], emptyPlace[1], num)) {    
             grid[emptyPlace[0]][emptyPlace[1]] = num;
             //recursively go for other rooms in the grid
             if (solveSudoku())     
                return true;
             //turn to unassigned space when conditions are not satisfied    
             grid[emptyPlace[0]][emptyPlace[1]] = 0;    
          }
       }
       return false;
    }
    public static void main(String[] args) {
       if (solveSudoku() == true)
          sudokuGrid();
       else
          System.out.println("Can't get a solution");
    }
}

# Define the size of the grid
N = 9

# Initialize the grid
grid = [
    [3, 1, 0, 5, 7, 8, 4, 0, 2],
    [0, 2, 9, 0, 3, 0, 0, 0, 8],
    [4, 0, 0, 6, 2, 9, 0, 3, 1],
    [2, 0, 3, 0, 1, 0, 0, 8, 0],
    [0, 7, 0, 8, 6, 3, 0, 0, 5],
    [8, 0, 1, 0, 9, 0, 6, 0, 0],
    [1, 3, 0, 0, 0, 0, 2, 5, 0],
    [6, 9, 2, 0, 5, 0, 0, 7, 4],
    [7, 0, 0, 2, 0, 6, 3, 0, 0]
]
# Check whether num is present in col or not
def isPresentInCol(col, num):
    for row in range(N):
        if grid[row][col] == num:
            return True
    return False

# Check whether num is present in row or not
def isPresentInRow(row, num):
    for col in range(N):
        if grid[row][col] == num:
            return True
    return False

# Check whether num is present in 3x3 box or not
def isPresentInBox(boxStartRow, boxStartCol, num):
    for row in range(3):
        for col in range(3):
            if grid[row+boxStartRow][col+boxStartCol] == num:
                return True
    return False

# Print the sudoku grid after solving
def sudokuGrid():
    for row in range(N):
        for col in range(N):
            if col == 3 or col == 6:
                print(" | ", end="")
            print(grid[row][col], end=" ")
        if row == 2 or row == 5:
            print("\n" + "---"*N)
        print()

# Get empty location and update row and column
def findEmptyPlace():
    for row in range(N):
        for col in range(N):
            # Marked with 0 is empty
            if grid[row][col] == 0:
                return row, col
    return None, None

def isValidPlace(row, col, num):
    # When item not found in col, row and current 3x3 box
    return not isPresentInRow(row, num) and not isPresentInCol(col, num) and not isPresentInBox(row - row%3, col - col%3, num)

def solveSudoku():
    row, col = findEmptyPlace()

    # When all places are filled
    if row is None and col is None:
        return True

    # Valid numbers are 1 - 9
    for num in range(1, 10):
        # Check validation, if yes, put the number in the grid
        if isValidPlace(row, col, num):
            grid[row][col] = num

            # Recursively go for other rooms in the grid
            if solveSudoku():
                return True

            # Turn to unassigned space when conditions are not satisfied
            grid[row][col] = 0

    return False

if __name__ == "__main__":
    if solveSudoku():
        sudokuGrid()
    else:
        print("Can't get a solution")

Output

3 1 6  | 5 7 8  | 4 9 2 
5 2 9  | 1 3 4  | 7 6 8 
4 8 7  | 6 2 9  | 5 3 1 
---------------------------
2 6 3  | 4 1 5  | 9 8 7 
9 7 4  | 8 6 3  | 1 2 5 
8 5 1  | 7 9 2  | 6 4 3 
---------------------------
1 3 8  | 9 4 7  | 2 5 6 
6 9 2  | 3 5 1  | 8 7 4 
7 4 5  | 2 8 6  | 3 1 9
Advertisements