Rabin Karp Algorithm

The Rabin-Karp algorithm is a pattern-matching algorithm that uses hashing to compare patterns and text. Here, the term Hashing refers to the process of mapping a larger input value to a smaller output value, called the hash value. This process will help in avoiding unnecessary comparison which optimizes the complexity of this algorithm. Therefore, the Rabin-Karp algorithm has a time complexity of O(n + m), where n is the length of the text and m is the length of the pattern.

How does Rabin Karp Algorithm work?

The Rabin-Karp algorithm checks the given pattern within a text by moving window one by one, but without checking all characters for all cases, it finds the hash value. Then, compare it with the hash values of all the substrings of the text that have the same length as the pattern.

If the hash values match, then there is a possibility that the pattern and the substring are equal, and we can verify it by comparing them character by character. If the hash values do not match, then we can skip the substring and move on to the next one. In the next section, we will understand how to calculate hash values.

Calculating hash value in Rabin Karp Algorithm

The steps to calculate hash values are as follows −

Step 1: Assign modulus and a base value

Suppose we have a text Txt = "DAACABCDBA" and a pattern Ptrn = "CAB". We will first assign numerical values to the characters of text based on their ranking. The leftmost character will have rank 1 and the rightmost ranks 10. Also, use base b = 10 (number of characters in the text) and modulus m = 11 for our hash function. It should be noted that the modulus m needs to be a prime number as it will help in avoiding overflow issues.

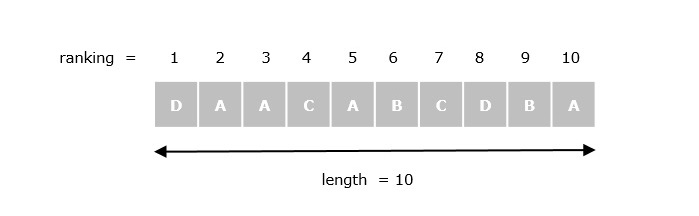
Ranking

Step 2: Calculate hash value of Pattern

The equation to calculate the hash value of the pattern is as follows −

  hash value(Ptrn) = Σ(r * bl-i-1) mod 11 
     where, r: ranking of character
            l: length of Pattern
            i: index of character within the pattern

Therefore, the hash value of Patrn is −

     h(Ptrn) = ((4 * 102) + (5 * 101) + (6 * 100)) mod 11 
             = 456 mod 11 
             = 5

Step 3: Calculate hash value of first Text window

Start calculating the hash value for all characters in the text by sliding over them. We will start with the first substring as shown below −

     h(DAA) = ((1 * 102) + (2 * 101) + (3 * 100)) mod 11 
            = 123 mod 11 
            = 6

Now, compare the hash value of pattern and the substring. If they match, check whether characters are matching or not. If they do, we found our match otherwise, move to the next characters.

In the above example, hash value did not matched. Hence, we move to the next character.

Step 4: Updating the hash value

Now, we need to remove the previous character and move to the next character. In this process, the hash value should also be updated till we find the match.

Example

The following example practically demonstrates the working of Rabin-Karp algorithm.

C C++ Java Python 
#include<stdio.h>
#include<string.h>
#define MAXCHAR 256 
// Function to perform Rabin-Karp algorithm
void rabinKSearch(char orgnlString[], char pattern[], int prime, int array[], int *index) {
   int patLen = strlen(pattern);
   int strLen = strlen(orgnlString);
   int charIndex, pattHash = 0, strHash = 0, h = 1; 
   // Calculate the value of helper variable
   for(int i = 0; i<patLen-1; i++) {
      h = (h*MAXCHAR) % prime;   
   }
   // Calculating initial hash values and first window 
   for(int i = 0; i<patLen; i++) {
      pattHash = (MAXCHAR*pattHash + pattern[i]) % prime;    
      strHash = (MAXCHAR*strHash + orgnlString[i]) % prime;   
   }
   // Slide the pattern over the text one by one
   for(int i = 0; i<=(strLen-patLen); i++) {
      // Check the hash values of current window of text and pattern
      if(pattHash == strHash) {      
         for(charIndex = 0; charIndex < patLen; charIndex++) {
            if(orgnlString[i+charIndex] != pattern[charIndex])
               break;
         }

         if(charIndex == patLen) {   
            (*index)++;
            array[(*index)] = i;
         }
      }
      // Calculating hash value for next window of text
      if(i < (strLen-patLen)) {    
         strHash = (MAXCHAR*(strHash - orgnlString[i]*h) + orgnlString[i+patLen])%prime;
         // If strHash is negative, convert it to positive
         if(strHash < 0) {
            strHash += prime;    
         }
      }
   }
}
int main() {
   char orgnlString[] = "AAAABCAEAAABCBDDAAAABC"; 
   char pattern[] = "AABC"; 
   int locArray[strlen(orgnlString)]; 
   int prime = 101; 
   int index = -1; 
   // Calling Rabin-Karp search function
   rabinKSearch(orgnlString, pattern, prime, locArray, &index); 
   for(int i = 0; i <= index; i++) {
      printf("Pattern found at position: %d\n", locArray[i]);
   }
   return 0;
}

#include<iostream> 
#define MAXCHAR 256 
using namespace std; 
// Function to perform Rabin-Karp algorithm
void rabinKSearch(string orgnlString, string pattern, int prime, int array[], int *index) {
   int patLen = pattern.size();
   int strLen = orgnlString.size();
   int charIndex, pattHash = 0, strHash = 0, h = 1; 
   // Calculate the value of helper variable
   for(int i = 0; i<patLen-1; i++) {
      h = (h*MAXCHAR) % prime;   
   }
   // Calculating initial hash values and first window 
   for(int i = 0; i<patLen; i++) {
      pattHash = (MAXCHAR*pattHash + pattern[i]) % prime;    
      strHash = (MAXCHAR*strHash + orgnlString[i]) % prime;   
   }
   // Slide the pattern over the text one by one
   for(int i = 0; i<=(strLen-patLen); i++) {
      // Check the hash values of current window of text and pattern
      if(pattHash == strHash) {      
         for(charIndex = 0; charIndex < patLen; charIndex++) {
            if(orgnlString[i+charIndex] != pattern[charIndex])
               break;
         }

         if(charIndex == patLen) {   
            (*index)++;
            array[(*index)] = i;
         }
      }
      // Calculating hash value for next window of text
      if(i < (strLen-patLen)) {    
         strHash = (MAXCHAR*(strHash - orgnlString[i]*h) + orgnlString[i+patLen])%prime;
         // If strHash is negative, convert it to positive
         if(strHash < 0) {
            strHash += prime;    
         }
      }
   }
}
int main() {
   string orgnlString = "AAAABCAEAAABCBDDAAAABC"; 
   // Pattern to be searched
   string pattern = "AABC"; 
   // Array to store the locations of the pattern
   int locArray[orgnlString.size()]; 
   int prime = 101; 
   int index = -1; 
   // Calling Rabin-Karp search function
   rabinKSearch(orgnlString, pattern, prime, locArray, &index); 
   // print the result
   for(int i = 0; i <= index; i++) {
      cout << "Pattern found at position: " << locArray[i]<<endl;
   }
}

import java.util.ArrayList;
public class Main {
   static final int MAXCHAR = 256;
   // method to perform Rabin-Karp algorithm
   static void rabinKSearch(String orgnlString, String pattern, int prime, ArrayList<Integer> locArray) {
      int patLen = pattern.length();
      int strLen = orgnlString.length();
      int charIndex, pattHash = 0, strHash = 0, h = 1;
      // Calculating value of helper variable
      for (int i = 0; i < patLen - 1; i++) {
         h = (h * MAXCHAR) % prime;
      }
      // Calculating initial hash values and first window 
      for (int i = 0; i < patLen; i++) {
         pattHash = (MAXCHAR * pattHash + pattern.charAt(i)) % prime;
         strHash = (MAXCHAR * strHash + orgnlString.charAt(i)) % prime;
      }
      // Slide the pattern over the text one by one 
      for (int i = 0; i <= (strLen - patLen); i++) {
         // Check the hash values of current window of text and pattern
         if (pattHash == strHash) {
            for (charIndex = 0; charIndex < patLen; charIndex++) {
               if (orgnlString.charAt(i + charIndex) != pattern.charAt(charIndex))
                  break;
            }

            if (charIndex == patLen) {
               locArray.add(i);
            }
         }
         // Calculating hash value for next window of text
         if (i < (strLen - patLen)) {
            strHash = (MAXCHAR * (strHash - orgnlString.charAt(i) * h) + orgnlString.charAt(i + patLen)) % prime;
            // If strHash is negative, convert it to positive
            if (strHash < 0) {
               strHash += prime;
            }
         }
      }
   }
   public static void main(String[] args) {
      String orgnlString = "AAAABCAEAAABCBDDAAAABC";
      // Pattern to be searched
      String pattern = "AABC";
      // Array to store the locations of the pattern
      ArrayList<Integer> locArray = new ArrayList<>();
      int prime = 101;
      // Calling Rabin-Karp method
      rabinKSearch(orgnlString, pattern, prime, locArray);
      // print the result
      for (int i = 0; i < locArray.size(); i++) {
         System.out.println("Pattern found at position: " + locArray.get(i));
      }
   }
}

MAXCHAR = 256 
# method to perform Rabin-Karp algorithm
def rabinKSearch(orgnlString, pattern, prime):
    patLen = len(pattern)
    strLen = len(orgnlString)
    pattHash = 0
    strHash = 0
    h = 1
    locArray = []
    # Calculating value of helper variable
    for i in range(patLen-1):
        h = (h*MAXCHAR) % prime
    # Calculating initial hash values and first window 
    for i in range(patLen):
        pattHash = (MAXCHAR*pattHash + ord(pattern[i])) % prime
        strHash = (MAXCHAR*strHash + ord(orgnlString[i])) % prime
    # Slide the pattern over the text one by one 
    for i in range(strLen-patLen+1):
        if pattHash == strHash:
            for charIndex in range(patLen):
                if orgnlString[i+charIndex] != pattern[charIndex]:
                    break
            else:
                locArray.append(i)
        # Calculating hash value for next window of text
        if i < strLen-patLen:
            strHash = (MAXCHAR*(strHash - ord(orgnlString[i])*h) + ord(orgnlString[i+patLen])) % prime
            if strHash < 0:
                strHash += prime

    return locArray

def main():
    orgnlString = "AAAABCAEAAABCBDDAAAABC"
    pattern = "AABC"
    prime = 101
    locArray = rabinKSearch(orgnlString, pattern, prime)
    for i in locArray:
        print(f"Pattern found at position: {i}")

if __name__ == "__main__":
    main()

Output

Pattern found at position: 2
Pattern found at position: 9
Pattern found at position: 18
Advertisements