
- DSA - Home
- DSA - Overview
- DSA - Environment Setup
- DSA - Algorithms Basics
- DSA - Asymptotic Analysis
- Data Structures
- DSA - Data Structure Basics
- DSA - Data Structures and Types
- DSA - Array Data Structure
- DSA - Skip List Data Structure
- Linked Lists
- DSA - Linked List Data Structure
- DSA - Doubly Linked List Data Structure
- DSA - Circular Linked List Data Structure
- Stack & Queue
- DSA - Stack Data Structure
- DSA - Expression Parsing
- DSA - Queue Data Structure
- DSA - Circular Queue Data Structure
- DSA - Priority Queue Data Structure
- DSA - Deque Data Structure
- Searching Algorithms
- DSA - Searching Algorithms
- DSA - Linear Search Algorithm
- DSA - Binary Search Algorithm
- DSA - Interpolation Search
- DSA - Jump Search Algorithm
- DSA - Exponential Search
- DSA - Fibonacci Search
- DSA - Sublist Search
- DSA - Hash Table
- Sorting Algorithms
- DSA - Sorting Algorithms
- DSA - Bubble Sort Algorithm
- DSA - Insertion Sort Algorithm
- DSA - Selection Sort Algorithm
- DSA - Merge Sort Algorithm
- DSA - Shell Sort Algorithm
- DSA - Heap Sort Algorithm
- DSA - Bucket Sort Algorithm
- DSA - Counting Sort Algorithm
- DSA - Radix Sort Algorithm
- DSA - Quick Sort Algorithm
- Matrices Data Structure
- DSA - Matrices Data Structure
- DSA - Lup Decomposition In Matrices
- DSA - Lu Decomposition In Matrices
- Graph Data Structure
- DSA - Graph Data Structure
- DSA - Depth First Traversal
- DSA - Breadth First Traversal
- DSA - Spanning Tree
- DSA - Topological Sorting
- DSA - Strongly Connected Components
- DSA - Biconnected Components
- DSA - Augmenting Path
- DSA - Network Flow Problems
- DSA - Flow Networks In Data Structures
- DSA - Edmonds Blossom Algorithm
- DSA - Maxflow Mincut Theorem
- Tree Data Structure
- DSA - Tree Data Structure
- DSA - Tree Traversal
- DSA - Binary Search Tree
- DSA - AVL Tree
- DSA - Red Black Trees
- DSA - B Trees
- DSA - B+ Trees
- DSA - Splay Trees
- DSA - Range Queries
- DSA - Segment Trees
- DSA - Fenwick Tree
- DSA - Fusion Tree
- DSA - Hashed Array Tree
- DSA - K-Ary Tree
- DSA - Kd Trees
- DSA - Priority Search Tree Data Structure
- Recursion
- DSA - Recursion Algorithms
- DSA - Tower of Hanoi Using Recursion
- DSA - Fibonacci Series Using Recursion
- Divide and Conquer
- DSA - Divide and Conquer
- DSA - Max-Min Problem
- DSA - Strassen's Matrix Multiplication
- DSA - Karatsuba Algorithm
- Greedy Algorithms
- DSA - Greedy Algorithms
- DSA - Travelling Salesman Problem (Greedy Approach)
- DSA - Prim's Minimal Spanning Tree
- DSA - Kruskal's Minimal Spanning Tree
- DSA - Dijkstra's Shortest Path Algorithm
- DSA - Map Colouring Algorithm
- DSA - Fractional Knapsack Problem
- DSA - Job Sequencing with Deadline
- DSA - Optimal Merge Pattern Algorithm
- Dynamic Programming
- DSA - Dynamic Programming
- DSA - Matrix Chain Multiplication
- DSA - Floyd Warshall Algorithm
- DSA - 0-1 Knapsack Problem
- DSA - Longest Common Sub-sequence Algorithm
- DSA - Travelling Salesman Problem (Dynamic Approach)
- Hashing
- DSA - Hashing Data Structure
- DSA - Collision In Hashing
- Disjoint Set
- DSA - Disjoint Set
- DSA - Path Compression And Union By Rank
- Heap
- DSA - Heap Data Structure
- DSA - Binary Heap
- DSA - Binomial Heap
- DSA - Fibonacci Heap
- Tries Data Structure
- DSA - Tries
- DSA - Standard Tries
- DSA - Compressed Tries
- DSA - Suffix Tries
- Treaps
- DSA - Treaps Data Structure
- Bit Mask
- DSA - Bit Mask In Data Structures
- Bloom Filter
- DSA - Bloom Filter Data Structure
- Approximation Algorithms
- DSA - Approximation Algorithms
- DSA - Vertex Cover Algorithm
- DSA - Set Cover Problem
- DSA - Travelling Salesman Problem (Approximation Approach)
- Randomized Algorithms
- DSA - Randomized Algorithms
- DSA - Randomized Quick Sort Algorithm
- DSA - Karger’s Minimum Cut Algorithm
- DSA - Fisher-Yates Shuffle Algorithm
- Miscellaneous
- DSA - Infix to Postfix
- DSA - Bellmon Ford Shortest Path
- DSA - Maximum Bipartite Matching
- DSA Useful Resources
- DSA - Questions and Answers
- DSA - Selection Sort Interview Questions
- DSA - Merge Sort Interview Questions
- DSA - Insertion Sort Interview Questions
- DSA - Heap Sort Interview Questions
- DSA - Bubble Sort Interview Questions
- DSA - Bucket Sort Interview Questions
- DSA - Radix Sort Interview Questions
- DSA - Cycle Sort Interview Questions
- DSA - Quick Guide
- DSA - Useful Resources
- DSA - Discussion
Matrix Chain Multiplication Algorithm
Matrix Chain Multiplication is an algorithm that is applied to determine the lowest cost way for multiplying matrices. The actual multiplication is done using the standard way of multiplying the matrices, i.e., it follows the basic rule that the number of rows in one matrix must be equal to the number of columns in another matrix. Hence, multiple scalar multiplications must be done to achieve the product.
To brief it further, consider matrices A, B, C, and D, to be multiplied; hence, the multiplication is done using the standard matrix multiplication. There are multiple combinations of the matrices found while using the standard approach since matrix multiplication is associative. For instance, there are five ways to multiply the four matrices given above −
(A(B(CD)))
(A((BC)D))
((AB)(CD))
((A(BC))D)
(((AB)C)D)
Now, if the size of matrices A, B, C, and D are l m, m n, n p, p q respectively, then the number of scalar multiplications performed will be lmnpq. But the cost of the matrices change based on the rows and columns present in it. Suppose, the values of l, m, n, p, q are 5, 10, 15, 20, 25 respectively, the cost of (A(B(CD))) is 5 100 25 = 12,500; however, the cost of (A((BC)D)) is 10 25 37 = 9,250.
So, dynamic programming approach of the matrix chain multiplication is adopted in order to find the combination with the lowest cost.
Matrix Chain Multiplication Algorithm
Matrix chain multiplication algorithm is only applied to find the minimum cost way to multiply a sequence of matrices. Therefore, the input taken by the algorithm is the sequence of matrices while the output achieved is the lowest cost parenthesization.
Algorithm
Count the number of parenthesizations. Find the number of ways in which the input matrices can be multiplied using the formulae −
$$P(n)=\left\{\begin{matrix} 1 & if\: n=1\\ \sum_{k=1}^{n-1} P(k)P(n-k)& if\: n\geq 2\\ \end{matrix}\right.$$
(or)
$$P(n)=\left\{\begin{matrix} \frac{2(n-1)C_{n-1}}{n} & if\: n\geq 2 \\ 1 & if\: n= 1\\ \end{matrix}\right.$$
Once the parenthesization is done, the optimal substructure must be devised as the first step of dynamic programming approach so the final product achieved is optimal. In matrix chain multiplication, the optimal substructure is found by dividing the sequence of matrices A[i.j] into two parts A[i,k] and A[k+1,j]. It must be ensured that the parts are divided in such a way that optimal solution is achieved.
Using the formula, $C[i,j]=\left\{\begin{matrix} 0 & if \: i=j\\ \displaystyle \min_{ i\leq k< j}\begin{cases} C [i,k]+C[k+1,j]+d_{i-1}d_{k}d_{j} \end{cases} &if \: i< j \\ \end{matrix}\right.$ find the lowest cost parenthesization of the sequence of matrices by constructing cost tables and corresponding k values table.
Once the lowest cost is found, print the corresponding parenthesization as the output.
Pseudocode
Pseudocode to find the lowest cost of all the possible parenthesizations −
MATRIX-CHAIN-MULTIPLICATION(p)
n = p.length 1
let m[1n, 1n] and s[1n 1, 2n] be new matrices
for i = 1 to n
m[i, i] = 0
for l = 2 to n // l is the chain length
for i = 1 to n - l + 1
j = i + l - 1
m[i, j] = ∞
for k = i to j - 1
q = m[i, k] + m[k + 1, j] + pi-1pkpj
if q < m[i, j]
m[i, j] = q
s[i, j] = k
return m and s
Pseudocode to print the optimal output parenthesization −
PRINT-OPTIMAL-OUTPUT(s, i, j ) if i == j print Ai else print ( PRINT-OPTIMAL-OUTPUT(s, i, s[i, j]) PRINT-OPTIMAL-OUTPUT(s, s[i, j] + 1, j) print )
Example
The application of dynamic programming formula is slightly different from the theory; to understand it better let us look at few examples below.
A sequence of matrices A, B, C, D with dimensions 5 10, 10 15, 15 20, 20 25 are set to be multiplied. Find the lowest cost parenthesization to multiply the given matrices using matrix chain multiplication.
Solution
Given matrices and their corresponding dimensions are −
A5×10×B10×15×C15×20×D20×25
Find the count of parenthesization of the 4 matrices, i.e. n = 4.
Using the formula, $P\left ( n \right )=\left\{\begin{matrix} 1 & if\: n=1\\ \sum_{k=1}^{n-1}P(k)P(n-k) & if\: n\geq 2 \\ \end{matrix}\right.$
Since n = 4 2, apply the second case of the formula −
$$P\left ( n \right )=\sum_{k=1}^{n-1}P(k)P(n-k)$$
$$P\left ( 4 \right )=\sum_{k=1}^{3}P(k)P(4-k)$$
$$P\left ( 4 \right )=P(1)P(3)+P(2)P(2)+P(3)P(1)$$
If P(1) = 1 and P(2) is also equal to 1, P(4) will be calculated based on the P(3) value. Therefore, P(3) needs to determined first.
$$P\left ( 3 \right )=P(1)P(2)+P(2)P(1)$$
$$=1+1=2$$
Therefore,
$$P\left ( 4 \right )=P(1)P(3)+P(2)P(2)+P(3)P(1)$$
$$=2+1+2=5$$
Among these 5 combinations of parenthesis, the matrix chain multiplicatiion algorithm must find the lowest cost parenthesis.
Step 1
The table above is known as a cost table, where all the cost values calculated from the different combinations of parenthesis are stored.
Another table is also created to store the k values obtained at the minimum cost of each combination.
Step 2
Applying the dynamic programming approach formula find the costs of various parenthesizations,
$$C[i,j]=\left\{\begin{matrix} 0 & if \: i=j\\ \displaystyle \min_{ i\leq k< j}\begin{cases} C [i,k]+C\left [ k+1,j \right ]+d_{i-1}d_{k}d_{j} \end{cases} &if \: i< j \\ \end{matrix}\right.$$
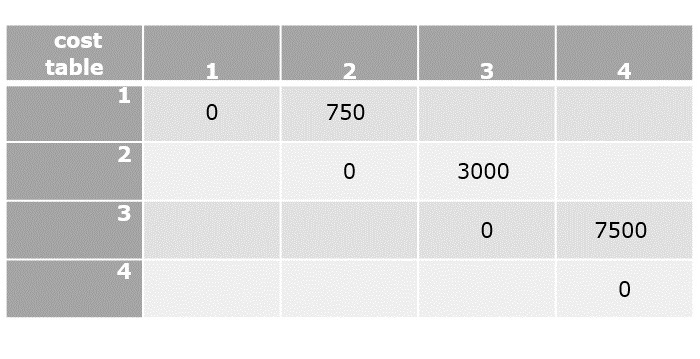
$C\left [ 1,1 \right ]=0$
$C\left [ 2,2 \right ]=0$
$C\left [ 3,3 \right ]=0$
$C\left [ 4,4 \right ]=0$
Step 3
Applying the dynamic approach formula only in the upper triangular values of the cost table, since i < j always.
$C[1,2]=\displaystyle \min_{ 1\leq k< 2}\begin{Bmatrix} C[1,1]+C[2,2]+d_{0}d_{1}d_{2} \end{Bmatrix}$
$C[1,2]=0+0+\left ( 5\times 10\times 15 \right )$
$C[1,2]=750$
$C[2,3]=\displaystyle \min_{ 2\leq k< 3}\begin{Bmatrix} C[2,2]+C[3,3]+d_{1}d_{2}d_{3} \end{Bmatrix}$
$C[2,3]=0+0+\left ( 10\times 15\times 20 \right )$
$C[2,3]=3000$
$C[3,4]=\displaystyle \min_{ 3\leq k< 4}\begin{Bmatrix} C[3,3]+C[4,4]+d_{2}d_{3}d_{4} \end{Bmatrix}$
$C[3,4]=0+0+\left ( 15\times 20\times 25 \right )$
$C[3,4]=7500$
Step 4
Find the values of [1, 3] and [2, 4] in this step. The cost table is always filled diagonally step-wise.
$C[2,4]=\displaystyle \min_{ 2\leq k< 4}\begin{Bmatrix} C[2,2]+C[3,4]+d_{1}d_{2}d_{4},C[2,3] +C[4,4]+d_{1}d_{3}d_{4}\end{Bmatrix}$
$C[2,4]=\displaystyle min\left\{ ( 0 + 7500 + (10 \times 15 \times 20)), (3000 + 5000)\right\}$
$C[2,4]=8000$
$C[1,3]=\displaystyle \min_{ 1\leq k< 3}\begin{Bmatrix} C[1,1]+C[2,3]+d_{0}d_{1}d_{3},C[1,2] +C[3,3]+d_{0}d_{2}d_{3}\end{Bmatrix}$
$C[1,3]=min\left\{ ( 0 + 3000 + 1000), (1500+0+750)\right\}$
$C[1,3]=2250$
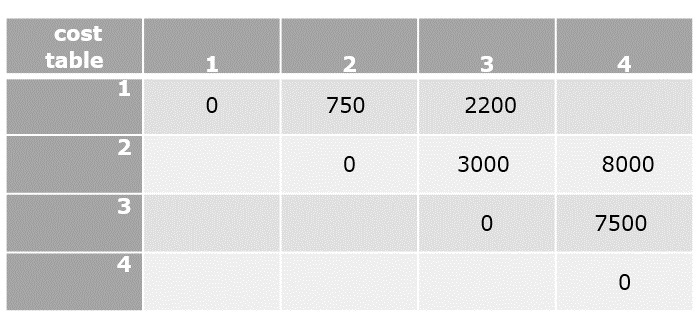
Step 5
Now compute the final element of the cost table to compare the lowest cost parenthesization.
$C[1,4]=\displaystyle \min_{ 1\leq k< 4}\begin{Bmatrix} C[1,1]+C[2,4]+d_{0}d_{1}d_{4},C[1,2] +C[3,4]+d_{1}d_{2}d_{4},C[1,3]+C[4,4] +d_{1}d_{3}d_{4}\end{Bmatrix}$
$C[1,4]=min\left\{0+8000+1250,750+7500+1875,2200+0+2500\right\}$
$C[1,4]=4700$
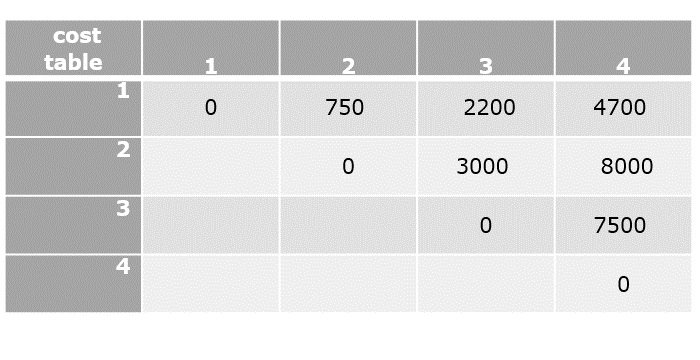
Now that all the values in cost table are computed, the final step is to parethesize the sequence of matrices. For that, k table needs to be constructed with the minimum value of k corresponding to every parenthesis.
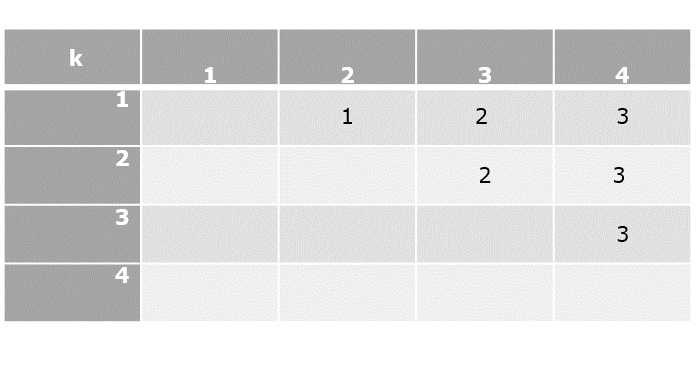
Parenthesization
Based on the lowest cost values from the cost table and their corresponding k values, let us add parenthesis on the sequence of matrices.
The lowest cost value at [1, 4] is achieved when k = 3, therefore, the first parenthesization must be done at 3.
(ABC)(D)
The lowest cost value at [1, 3] is achieved when k = 2, therefore the next parenthesization is done at 2.
((AB)C)(D)
The lowest cost value at [1, 2] is achieved when k = 1, therefore the next parenthesization is done at 1. But the parenthesization needs at least two matrices to be multiplied so we do not divide further.
((AB)(C))(D)
Since, the sequence cannot be parenthesized further, the final solution of matrix chain multiplication is ((AB)C)(D).
Implementation
Following is the final implementation of Matrix Chain Multiplication Algorithm to calculate the minimum number of ways several matrices can be multiplied using dynamic programming −
#include <stdio.h>
#include <string.h>
#define INT_MAX 999999
int mc[50][50];
int min(int a, int b){
if(a < b)
return a;
else
return b;
}
int DynamicProgramming(int c[], int i, int j){
if (i == j) {
return 0;
}
if (mc[i][j] != -1) {
return
mc[i][j];
}
mc[i][j] = INT_MAX;
for (int k = i; k < j; k++) {
mc[i][j] = min(mc[i][j], DynamicProgramming(c, i, k) + DynamicProgramming(c, k + 1, j) + c[i - 1] * c[k] * c[j]);
}
return mc[i][j];
}
int Matrix(int c[], int n){
int i = 1, j = n - 1;
return DynamicProgramming(c, i, j);
}
int main(){
int arr[] = { 23, 26, 27, 20 };
int n = sizeof(arr) / sizeof(arr[0]);
memset(mc, -1, sizeof mc);
printf("Minimum number of multiplications is: %d", Matrix(arr, n));
}
Output
Minimum number of multiplications is: 26000
#include <bits/stdc++.h>
using namespace std;
int mc[50][50];
int DynamicProgramming(int* c, int i, int j){
if (i == j) {
return 0;
}
if (mc[i][j] != -1) {
return
mc[i][j];
}
mc[i][j] = INT_MAX;
for (int k = i; k < j; k++) {
mc[i][j] = min(mc[i][j], DynamicProgramming(c, i, k) + DynamicProgramming(c, k + 1, j) + c[i - 1] * c[k] * c[j]);
}
return mc[i][j];
}
int Matrix(int* c, int n){
int i = 1, j = n - 1;
return DynamicProgramming(c, i, j);
}
int main(){
int arr[] = { 23, 26, 27, 20 };
int n = sizeof(arr) / sizeof(arr[0]);
memset(mc, -1, sizeof mc);
cout << "Minimum number of multiplications is: " << Matrix(arr, n);
}
Output
Minimum number of multiplications is: 26000
import java.io.*;
import java.util.*;
public class Main {
static int[][] mc = new int[50][50];
public static int DynamicProgramming(int c[], int i, int j) {
if (i == j) {
return 0;
}
if (mc[i][j] != -1) {
return mc[i][j];
}
mc[i][j] = Integer.MAX_VALUE;
for (int k = i; k < j; k++) {
mc[i][j] = Math.min(mc[i][j], DynamicProgramming(c, i, k) + DynamicProgramming(c, k + 1, j) + c[i - 1] * c[k] * c[j]);
}
return mc[i][j];
}
public static int Matrix(int c[], int n) {
int i = 1, j = n - 1;
return DynamicProgramming(c, i, j);
}
public static void main(String args[]) {
int arr[] = { 23, 26, 27, 20 };
int n = arr.length;
for (int[] row : mc)
Arrays.fill(row, -1);
System.out.println("Minimum number of multiplications is: " + Matrix(arr, n));
}
}
Output
Minimum number of multiplications is: 26000
mc = [[-1 for n in range(50)] for m in range(50)]
def DynamicProgramming(c, i, j):
if (i == j):
return 0
if (mc[i][j] != -1):
return mc[i][j]
mc[i][j] = 999999
for k in range (i, j):
mc[i][j] = min(mc[i][j], DynamicProgramming(c, i, k) + DynamicProgramming(c, k + 1, j) + c[i - 1] * c[k] * c[j]);
return mc[i][j]
def Matrix(c, n):
i = 1
j = n - 1
return DynamicProgramming(c, i, j);
arr = [ 23, 26, 27, 20 ]
n = len(arr)
print("Minimum number of multiplications is: ")
print(Matrix(arr, n))
Output
Minimum number of multiplications is: 26000
