M-Coloring Problem

Previous
Quiz
Next

What is M-Coloring Problem?

In the M-Coloring problem, our task is to find if it is possible to assign nodes of a given graph with m different colors, such that no two adjacent vertices of the graph are of the same colors. If a solution exists, then display which color is assigned to each vertex. The m-coloring problem is practically used to solve problems like clustering, scheduling, job allocation problems and many more.

A graph is an abstract data type (ADT) consisting of a set of objects that are connected via links.

Input Output Scenario

Suppose the given undirected graph G(V, E) and its adjacency matrix are as follows −

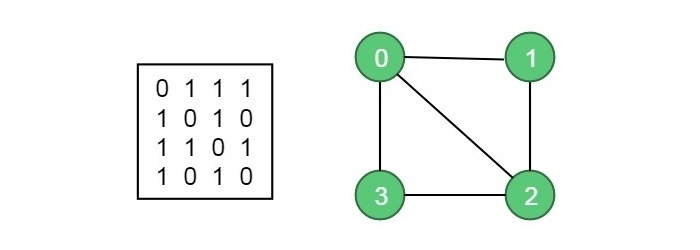
M-Coloring

Let the maximum color m = 3, which indicates the maximum number of colors that can be used. The backtracking algorithm can be used to solve the m-coloring problem for the above graph. This algorithm will return which node will be assigned with which color. If the solution is not possible, it will return false.

For this case, the output should be Node 0 -> color 1, Node 1 -> color 2, Node 2 -> color 3, Node 3 -> color 2. The figure below illustrates the same −

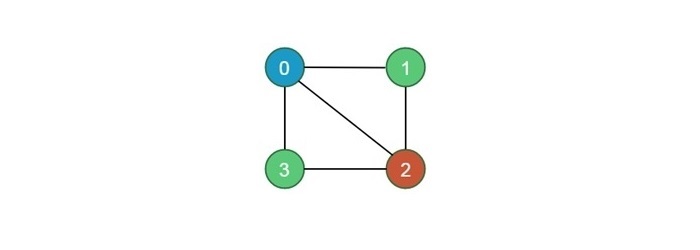
M-Coloring output

Solving M-Coloring Problem using Backtracking Approach

The naive way to solve m-coloring problem is by generating all possible combinations of vertices with colors and checking if any combination satisfies the given constraints. However, this approach is inefficient for larger graphs.

To solve m-coloring problem using the backtracking approach, follow the below steps −

  • Starting from vertex 0, we will try to assign colors one by one to different nodes.

  • However, before assigning, we have to check whether the color is safe or not. Color is not safe when adjacent vertices contain the same color.

  • Next, we will check if is there any color assignment that satisfies the constraint. If it does, we mark that assignment as a solution to the m-coloring problem.

Example

In the following example, we will illustrate how to solve the m-coloring problem in a given undirected graph.

C C++ Java Python 
#include <stdio.h>
#include <stdlib.h> 
#include <stdbool.h>
#define V 4
bool graph[V][V] = {
   {0, 1, 1, 1},
   {1, 0, 1, 0},
   {1, 1, 0, 1},
   {1, 0, 1, 0}
};
void showColors(int color[]) {
   printf("Assigned Colors are:\n");
   for (int i = 0; i < V; i++)
      printf("%d ", color[i]);
   printf("\n");
}
//check whether putting a color valid for v
bool isValid(int v, int color[], int c) {
   for (int i = 0; i < V; i++)
      if (graph[v][i] && c == color[i])
         return false;
   return true;
}
bool graphColoring(int colors, int color[], int vertex) {
   //when all vertices are considered      
   if (vertex == V)
      return true;
   for (int col = 1; col <= colors; col++) {
      //check whether color is valid or not 
      if (isValid(vertex, color, col)) {
         color[vertex] = col;
         // go for additional vertices
         if (graphColoring(colors, color, vertex + 1))
            return true;
         color[vertex] = 0;
      }
   }
   //when no colors can be assigned
   return false;
}
bool checkSolution(int m) {
   //make color matrix for each vertex   
   int *color = (int *)malloc(V * sizeof(int)); 
   for (int i = 0; i < V; i++)
      //initially set to 0
      color[i] = 0;
   //for vertex 0 check graph coloring      
   if (graphColoring(m, color, 0) == false) {
      printf("Solution does not exist.\n");
      free(color); 
      return false;
   }
   showColors(color);
   free(color); 
   return true;
}

int main() {
   // Number of colors    
   int colors = 3;
   checkSolution(colors);
   return 0;
}

#include<iostream>
#define V 4
using namespace std;
bool graph[V][V] = {
   {0, 1, 1, 1},
   {1, 0, 1, 0},
   {1, 1, 0, 1},
   {1, 0, 1, 0},
};
void showColors(int color[]) {
   cout << "Assigned Colors are: " <<endl;
   for (int i = 0; i < V; i++)
      cout << color[i] << " ";
   cout << endl;
}
//check whether putting a color valid for v
bool isValid(int v,int color[], int c) {    
   for (int i = 0; i < V; i++)
      if (graph[v][i] && c == color[i])
         return false;
   return true;
}
bool graphColoring(int colors, int color[], int vertex) {
   //when all vertices are considered    
   if (vertex == V)    
      return true;
   for (int col = 1; col <= colors; col++) {
      //check whether color is valid or not 
      if (isValid(vertex,color, col)) {     
         color[vertex] = col;
         // go for additional vertices
         if (graphColoring (colors, color, vertex+1) == true)    
            return true;
                   
         color[vertex] = 0;
      }
   }
   //when no colors can be assigned
   return false; 
}
bool checkSolution(int m) {
   //make color matrix for each vertex    
   int *color = new int[V];    
   for (int i = 0; i < V; i++)
      //initially set to 0
      color[i] = 0;      
   //for vertex 0 check graph coloring
   if (graphColoring(m, color, 0) == false) {    
      cout << "Solution does not exist.";
      return false;
   }
   showColors(color);
   return true;
}
int main() {
   // Number of colors    
   int colors = 3;      
   checkSolution (colors);
}

public class GraphColoring {
   static final int V = 4;
   static boolean[][] graph = {
      {false, true, true, true},
      {true, false, true, false},
      {true, true, false, true},
      {true, false, true, false}
   };
   static void showColors(int[] color) {
      System.out.println("Assigned Colors are:");
      for (int i = 0; i < V; i++) {
         System.out.print(color[i] + " ");
      }
      System.out.println();
   }
   //check whether putting a color valid for v
   static boolean isValid(int v, int[] color, int c) {
      for (int i = 0; i < V; i++) {
         if (graph[v][i] && c == color[i]) {
            return false;
         }
      }
      return true;
   }
   static boolean graphColoring(int colors, int[] color, int vertex) {
      //when all vertices are considered    
      if (vertex == V) {
         return true;
      }
      for (int col = 1; col <= colors; col++) {
         //check whether color is valid or not 
         if (isValid(vertex, color, col)) {
            color[vertex] = col;
            // go for additional vertices
            if (graphColoring(colors, color, vertex + 1)) {
               return true;
            }
            color[vertex] = 0;
         }
      }
      //when no colors can be assigned
        return false;
   }
   static boolean checkSolution(int m) {
      //make color matrix for each vertex 
      int[] color = new int[V];
      for (int i = 0; i < V; i++) {
         //initially set to 0
         color[i] = 0;
      }
      //for vertex 0 check graph coloring
      if (!graphColoring(m, color, 0)) {
         System.out.println("Solution does not exist.");
         return false;
      }
      showColors(color);
      return true;
   }
   public static void main(String[] args) {
      // Number of colors 
      int colors = 3;
      checkSolution(colors);
   }
}

V = 4
graph = [
    [0, 1, 1, 1],
    [1, 0, 1, 0],
    [1, 1, 0, 1],
    [1, 0, 1, 0]
]
def show_colors(color):
    print("Assigned Colors are:")
    for i in range(V):
        print(color[i], end=" ")
    print()

def is_valid(v, color, c):
    for i in range(V):
        if graph[v][i] and c == color[i]:
            return False
    return True

def graph_coloring(colors, color, vertex):
    if vertex == V:
        return True
    for col in range(1, colors + 1):
        if is_valid(vertex, color, col):
            color[vertex] = col
            if graph_coloring(colors, color, vertex + 1):
                return True
            color[vertex] = 0
    return False

def check_solution(m):
    color = [0] * V
    if not graph_coloring(m, color, 0):
        print("Solution does not exist.")
        return False
    show_colors(color)
    return True

if __name__ == "__main__":
    colors = 3
    check_solution(colors)

Output

Assigned Colors are: 
1 2 3 2
Print Page
Previous
Next
Advertisements