
- DSA - Home
- DSA - Overview
- DSA - Environment Setup
- DSA - Algorithms Basics
- DSA - Asymptotic Analysis
- Data Structures
- DSA - Data Structure Basics
- DSA - Data Structures and Types
- DSA - Array Data Structure
- DSA - Skip List Data Structure
- Linked Lists
- DSA - Linked List Data Structure
- DSA - Doubly Linked List Data Structure
- DSA - Circular Linked List Data Structure
- Stack & Queue
- DSA - Stack Data Structure
- DSA - Expression Parsing
- DSA - Queue Data Structure
- DSA - Circular Queue Data Structure
- DSA - Priority Queue Data Structure
- DSA - Deque Data Structure
- Searching Algorithms
- DSA - Searching Algorithms
- DSA - Linear Search Algorithm
- DSA - Binary Search Algorithm
- DSA - Interpolation Search
- DSA - Jump Search Algorithm
- DSA - Exponential Search
- DSA - Fibonacci Search
- DSA - Sublist Search
- DSA - Hash Table
- Sorting Algorithms
- DSA - Sorting Algorithms
- DSA - Bubble Sort Algorithm
- DSA - Insertion Sort Algorithm
- DSA - Selection Sort Algorithm
- DSA - Merge Sort Algorithm
- DSA - Shell Sort Algorithm
- DSA - Heap Sort Algorithm
- DSA - Bucket Sort Algorithm
- DSA - Counting Sort Algorithm
- DSA - Radix Sort Algorithm
- DSA - Quick Sort Algorithm
- Matrices Data Structure
- DSA - Matrices Data Structure
- DSA - Lup Decomposition In Matrices
- DSA - Lu Decomposition In Matrices
- Graph Data Structure
- DSA - Graph Data Structure
- DSA - Depth First Traversal
- DSA - Breadth First Traversal
- DSA - Spanning Tree
- DSA - Topological Sorting
- DSA - Strongly Connected Components
- DSA - Biconnected Components
- DSA - Augmenting Path
- DSA - Network Flow Problems
- DSA - Flow Networks In Data Structures
- DSA - Edmonds Blossom Algorithm
- DSA - Maxflow Mincut Theorem
- Tree Data Structure
- DSA - Tree Data Structure
- DSA - Tree Traversal
- DSA - Binary Search Tree
- DSA - AVL Tree
- DSA - Red Black Trees
- DSA - B Trees
- DSA - B+ Trees
- DSA - Splay Trees
- DSA - Range Queries
- DSA - Segment Trees
- DSA - Fenwick Tree
- DSA - Fusion Tree
- DSA - Hashed Array Tree
- DSA - K-Ary Tree
- DSA - Kd Trees
- DSA - Priority Search Tree Data Structure
- Recursion
- DSA - Recursion Algorithms
- DSA - Tower of Hanoi Using Recursion
- DSA - Fibonacci Series Using Recursion
- Divide and Conquer
- DSA - Divide and Conquer
- DSA - Max-Min Problem
- DSA - Strassen's Matrix Multiplication
- DSA - Karatsuba Algorithm
- Greedy Algorithms
- DSA - Greedy Algorithms
- DSA - Travelling Salesman Problem (Greedy Approach)
- DSA - Prim's Minimal Spanning Tree
- DSA - Kruskal's Minimal Spanning Tree
- DSA - Dijkstra's Shortest Path Algorithm
- DSA - Map Colouring Algorithm
- DSA - Fractional Knapsack Problem
- DSA - Job Sequencing with Deadline
- DSA - Optimal Merge Pattern Algorithm
- Dynamic Programming
- DSA - Dynamic Programming
- DSA - Matrix Chain Multiplication
- DSA - Floyd Warshall Algorithm
- DSA - 0-1 Knapsack Problem
- DSA - Longest Common Sub-sequence Algorithm
- DSA - Travelling Salesman Problem (Dynamic Approach)
- Hashing
- DSA - Hashing Data Structure
- DSA - Collision In Hashing
- Disjoint Set
- DSA - Disjoint Set
- DSA - Path Compression And Union By Rank
- Heap
- DSA - Heap Data Structure
- DSA - Binary Heap
- DSA - Binomial Heap
- DSA - Fibonacci Heap
- Tries Data Structure
- DSA - Tries
- DSA - Standard Tries
- DSA - Compressed Tries
- DSA - Suffix Tries
- Treaps
- DSA - Treaps Data Structure
- Bit Mask
- DSA - Bit Mask In Data Structures
- Bloom Filter
- DSA - Bloom Filter Data Structure
- Approximation Algorithms
- DSA - Approximation Algorithms
- DSA - Vertex Cover Algorithm
- DSA - Set Cover Problem
- DSA - Travelling Salesman Problem (Approximation Approach)
- Randomized Algorithms
- DSA - Randomized Algorithms
- DSA - Randomized Quick Sort Algorithm
- DSA - Karger’s Minimum Cut Algorithm
- DSA - Fisher-Yates Shuffle Algorithm
- Miscellaneous
- DSA - Infix to Postfix
- DSA - Bellmon Ford Shortest Path
- DSA - Maximum Bipartite Matching
- DSA Useful Resources
- DSA - Questions and Answers
- DSA - Selection Sort Interview Questions
- DSA - Merge Sort Interview Questions
- DSA - Insertion Sort Interview Questions
- DSA - Heap Sort Interview Questions
- DSA - Bubble Sort Interview Questions
- DSA - Bucket Sort Interview Questions
- DSA - Radix Sort Interview Questions
- DSA - Cycle Sort Interview Questions
- DSA - Quick Guide
- DSA - Useful Resources
- DSA - Discussion
Interpolation Search Algorithm
Interpolation search is an improved variant of binary search. This search algorithm works on the probing position of the required value. For this algorithm to work properly, the data collection should be in a sorted form and equally distributed.
Binary search has a huge advantage of time complexity over linear search. Linear search has worst-case complexity of (n) whereas binary search has (log n).
There are cases where the location of target data may be known in advance. For example, in case of a telephone directory, if we want to search the telephone number of Morpheus. Here, linear search and even binary search will seem slow as we can directly jump to memory space where the names start from 'M' are stored.
Positioning in Binary Search
In binary search, if the desired data is not found then the rest of the list is divided in two parts, lower and higher. The search is carried out in either of them.
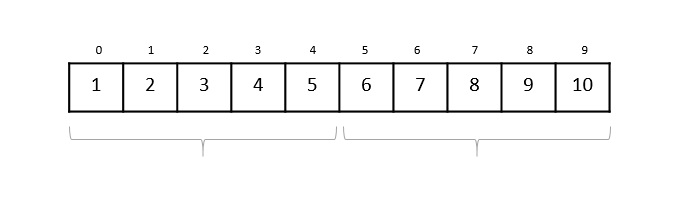
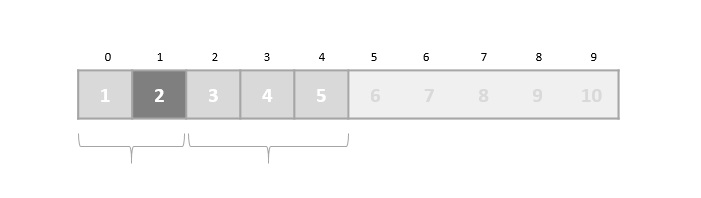
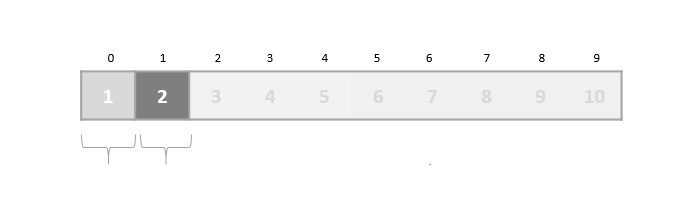
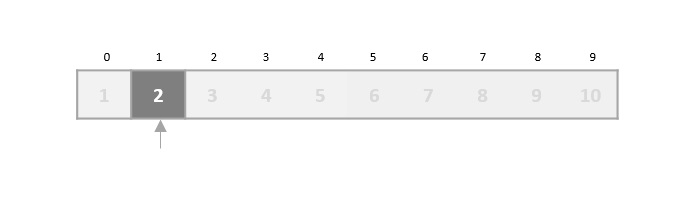
Even when the data is sorted, binary search does not take advantage to probe the position of the desired data.
Position Probing in Interpolation Search
Interpolation search finds a particular item by computing the probe position. Initially, the probe position is the position of the middle most item of the collection.


If a match occurs, then the index of the item is returned. To split the list into two parts, we use the following method −
$$mid\, =\, Lo\, +\, \frac{\left ( Hi\, -\, Lo \right )\ast \left ( X\, -\, A\left [ Lo \right ] \right )}{A\left [ Hi \right ]\, -\, A\left [ Lo \right ]}$$
where −
A = list Lo = Lowest index of the list Hi = Highest index of the list A[n] = Value stored at index n in the list
If the middle item is greater than the item, then the probe position is again calculated in the sub-array to the right of the middle item. Otherwise, the item is searched in the sub-array to the left of the middle item. This process continues on the sub-array as well until the size of subarray reduces to zero.
Interpolation Search Algorithm
As it is an improvisation of the existing BST algorithm, we are mentioning the steps to search the 'target' data value index, using position probing −
1. Start searching data from middle of the list. 2. If it is a match, return the index of the item, and exit. 3. If it is not a match, probe position. 4. Divide the list using probing formula and find the new middle. 5. If data is greater than middle, search in higher sub-list. 6. If data is smaller than middle, search in lower sub-list. 7. Repeat until match.
Pseudocode
A → Array list
N → Size of A
X → Target Value
Procedure Interpolation_Search()
Set Lo → 0
Set Mid → -1
Set Hi → N-1
While X does not match
if Lo equals to Hi OR A[Lo] equals to A[Hi]
EXIT: Failure, Target not found
end if
Set Mid = Lo + ((Hi - Lo) / (A[Hi] - A[Lo])) * (X - A[Lo])
if A[Mid] = X
EXIT: Success, Target found at Mid
else
if A[Mid] < X
Set Lo to Mid+1
else if A[Mid] > X
Set Hi to Mid-1
end if
end if
End While
End Procedure
Analysis
Runtime complexity of interpolation search algorithm is (log (log n)) as compared to (log n) of BST in favorable situations.
Example
To understand the step-by-step process involved in the interpolation search, let us look at an example and work around it.
Consider an array of sorted elements given below −
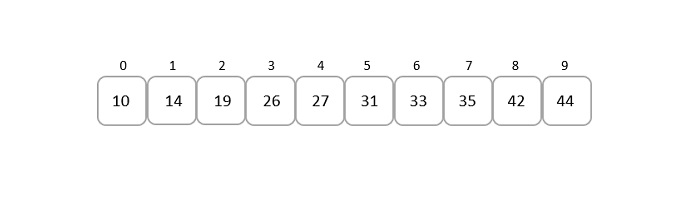
Let us search for the element 19.
Solution
Unlike binary search, the middle point in this approach is chosen using the formula −
$$mid\, =\, Lo\, +\, \frac{\left ( Hi\, -\, Lo \right )\ast \left ( X\, -\, A\left [ Lo \right ] \right )}{A\left [ Hi \right ]\, -\, A\left [ Lo \right ]}$$
So in this given array input,
Lo = 0, A[Lo] = 10 Hi = 9, A[Hi] = 44 X = 19
Applying the formula to find the middle point in the list, we get
$$mid\, =\, 0\, +\, \frac{\left ( 9\, -\, 0 \right )\ast \left ( 19\, -\, 10 \right )}{44\, -\, 10}$$
$$mid\, =\, \frac{9\ast 9}{34}$$
$$mid\, =\, \frac{81}{34}\,=\,2.38$$
Since, mid is an index value, we only consider the integer part of the decimal. That is, mid = 2.
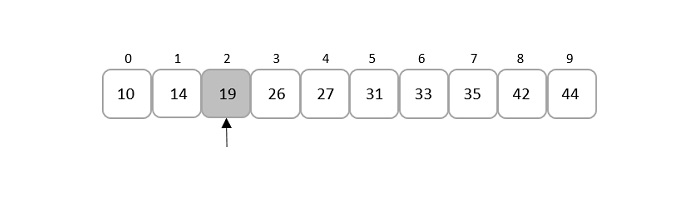
Comparing the key element given, that is 19, to the element present in the mid index, it is found that both the elements match.
Therefore, the element is found at index 2.
Implementation
Interpolation search is an improved variant of binary search. This search algorithm works on the probing position of the required value. For this algorithm to work properly, the data collection should be in sorted and equally distributed form.
#include<stdio.h>
#define MAX 10
// array of items on which linear search will be conducted.
int list[MAX] = { 10, 14, 19, 26, 27, 31, 33, 35, 42, 44 };
int interpolation_search(int data){
int lo = 0;
int hi = MAX - 1;
int mid = -1;
int comparisons = 1;
int index = -1;
while(lo <= hi) {
printf("Comparison %d \n" , comparisons ) ;
printf("lo : %d, list[%d] = %d\n", lo, lo, list[lo]);
printf("hi : %d, list[%d] = %d\n", hi, hi, list[hi]);
comparisons++;
// probe the mid point
mid = lo + (((double)(hi - lo) / (list[hi] - list[lo])) * (data - list[lo]));
printf("mid = %d\n",mid);
// data found
if(list[mid] == data) {
index = mid;
break;
} else {
if(list[mid] < data) {
// if data is larger, data is in upper half
lo = mid + 1;
} else {
// if data is smaller, data is in lower half
hi = mid - 1;
}
}
}
printf("Total comparisons made: %d", --comparisons);
return index;
}
int main(){
//find location of 33
int location = interpolation_search(33);
// if element was found
if(location != -1)
printf("\nElement found at location: %d" ,(location+1));
else
printf("Element not found.");
return 0;
}
Output
Comparison 1 lo : 0, list[0] = 10 hi : 9, list[9] = 44 mid = 6 Total comparisons made: 1 Element found at location: 7
#include<iostream>
using namespace std;
#define MAX 10
// array of items on which linear search will be conducted.
int list[MAX] = { 10, 14, 19, 26, 27, 31, 33, 35, 42, 44 };
int interpolation_search(int data){
int lo = 0;
int hi = MAX - 1;
int mid = -1;
int comparisons = 1;
int index = -1;
while(lo <= hi) {
cout << "Comparison " << comparisons << endl;
cout << "lo : " << lo << " list[" << lo << "] = " << list[lo] << endl;
cout << "hi : " << hi << " list[" << hi << "] = " << list[hi] << endl;
comparisons++;
// probe the mid point
mid = lo + (((double)(hi - lo) / (list[hi] - list[lo])) * (data - list[lo]));
cout << "mid = " << mid;
// data found
if(list[mid] == data) {
index = mid;
break;
} else {
if(list[mid] < data) {
// if data is larger, data is in upper half
lo = mid + 1;
} else {
// if data is smaller, data is in lower half
hi = mid - 1;
}
}
}
cout << "\nTotal comparisons made: " << (--comparisons);
return index;
}
int main(){
//find location of 33
int location = interpolation_search(33);
// if element was found
if(location != -1)
cout << "\nElement found at location: " << (location+1);
else
cout << "Element not found.";
return 0;
}
Output
Comparison 1 lo : 0 list[0] = 10 hi : 9 list[9] = 44 mid = 6 Total comparisons made: 1 Element found at location: 7
import java.io.*;
public class InterpolationSearch {
static int interpolation_search(int data, int[] list) {
int lo = 0;
int hi = list.length - 1;
int mid = -1;
int comparisons = 1;
int index = -1;
while(lo <= hi) {
System.out.println("Comparison " + comparisons);
System.out.println("lo : " + lo + " list[" + lo + "] = " + list[lo]);
System.out.println("hi : " + hi + " list[" + hi + "] = " + list[hi]);
comparisons++;
// probe the mid point
mid = lo + (((hi - lo) * (data - list[lo])) / (list[hi] - list[lo]));
System.out.println("mid = " + mid);
// data found
if(list[mid] == data) {
index = mid;
break;
} else {
if(list[mid] < data) {
// if data is larger, data is in upper half
lo = mid + 1;
} else {
// if data is smaller, data is in lower half
hi = mid - 1;
}
}
}
System.out.println("Total comparisons made: " + (--comparisons));
return index;
}
public static void main(String args[]) {
int[] list = { 10, 14, 19, 26, 27, 31, 33, 35, 42, 44 };
//find location of 33
int location = interpolation_search(33, list);
// if element was found
if(location != -1)
System.out.println("Element found at location: " + (location+1));
else
System.out.println("Element not found.");
}
}
Output
Comparison 1 lo : 0 list[0] = 10 hi : 9 list[9] = 44 mid = 6 Total comparisons made: 1 Element found at location: 7
def interpolation_search( data, arr):
lo = 0
hi = len(arr) - 1
mid = -1
comparisons = 1
index = -1
while(lo <= hi):
print("Comparison ", comparisons)
print("lo : ", lo)
print("list[", lo, "] = ")
print(arr[lo])
print("hi : ", hi)
print("list[", hi, "] = ")
print(arr[hi])
comparisons = comparisons + 1
#probe the mid point
mid = lo + (((hi - lo) * (data - arr[lo])) // (arr[hi] - arr[lo]))
print("mid = ", mid)
#data found
if(arr[mid] == data):
index = mid
break
else:
if(arr[mid] < data):
#if data is larger, data is in upper half
lo = mid + 1
else:
#if data is smaller, data is in lower half
hi = mid - 1
print("Total comparisons made: ")
print(comparisons-1)
return index
arr = [10, 14, 19, 26, 27, 31, 33, 35, 42, 44]
#find location of 33
location = interpolation_search(33, arr)
#if element was found
if(location != -1):
print("Element found at location: ", (location+1))
else:
print("Element not found.")
Output
Comparison 1 lo : 0 list[ 0 ] = 10 hi : 9 list[ 9 ] = 44 mid = 6 Total comparisons made: 1 Element found at location: 7
