
- DSA - Home
- DSA - Overview
- DSA - Environment Setup
- DSA - Algorithms Basics
- DSA - Asymptotic Analysis
- Data Structures
- DSA - Data Structure Basics
- DSA - Data Structures and Types
- DSA - Array Data Structure
- DSA - Skip List Data Structure
- Linked Lists
- DSA - Linked List Data Structure
- DSA - Doubly Linked List Data Structure
- DSA - Circular Linked List Data Structure
- Stack & Queue
- DSA - Stack Data Structure
- DSA - Expression Parsing
- DSA - Queue Data Structure
- DSA - Circular Queue Data Structure
- DSA - Priority Queue Data Structure
- DSA - Deque Data Structure
- Searching Algorithms
- DSA - Searching Algorithms
- DSA - Linear Search Algorithm
- DSA - Binary Search Algorithm
- DSA - Interpolation Search
- DSA - Jump Search Algorithm
- DSA - Exponential Search
- DSA - Fibonacci Search
- DSA - Sublist Search
- DSA - Hash Table
- Sorting Algorithms
- DSA - Sorting Algorithms
- DSA - Bubble Sort Algorithm
- DSA - Insertion Sort Algorithm
- DSA - Selection Sort Algorithm
- DSA - Merge Sort Algorithm
- DSA - Shell Sort Algorithm
- DSA - Heap Sort Algorithm
- DSA - Bucket Sort Algorithm
- DSA - Counting Sort Algorithm
- DSA - Radix Sort Algorithm
- DSA - Quick Sort Algorithm
- Matrices Data Structure
- DSA - Matrices Data Structure
- DSA - Lup Decomposition In Matrices
- DSA - Lu Decomposition In Matrices
- Graph Data Structure
- DSA - Graph Data Structure
- DSA - Depth First Traversal
- DSA - Breadth First Traversal
- DSA - Spanning Tree
- DSA - Topological Sorting
- DSA - Strongly Connected Components
- DSA - Biconnected Components
- DSA - Augmenting Path
- DSA - Network Flow Problems
- DSA - Flow Networks In Data Structures
- DSA - Edmonds Blossom Algorithm
- DSA - Maxflow Mincut Theorem
- Tree Data Structure
- DSA - Tree Data Structure
- DSA - Tree Traversal
- DSA - Binary Search Tree
- DSA - AVL Tree
- DSA - Red Black Trees
- DSA - B Trees
- DSA - B+ Trees
- DSA - Splay Trees
- DSA - Range Queries
- DSA - Segment Trees
- DSA - Fenwick Tree
- DSA - Fusion Tree
- DSA - Hashed Array Tree
- DSA - K-Ary Tree
- DSA - Kd Trees
- DSA - Priority Search Tree Data Structure
- Recursion
- DSA - Recursion Algorithms
- DSA - Tower of Hanoi Using Recursion
- DSA - Fibonacci Series Using Recursion
- Divide and Conquer
- DSA - Divide and Conquer
- DSA - Max-Min Problem
- DSA - Strassen's Matrix Multiplication
- DSA - Karatsuba Algorithm
- Greedy Algorithms
- DSA - Greedy Algorithms
- DSA - Travelling Salesman Problem (Greedy Approach)
- DSA - Prim's Minimal Spanning Tree
- DSA - Kruskal's Minimal Spanning Tree
- DSA - Dijkstra's Shortest Path Algorithm
- DSA - Map Colouring Algorithm
- DSA - Fractional Knapsack Problem
- DSA - Job Sequencing with Deadline
- DSA - Optimal Merge Pattern Algorithm
- Dynamic Programming
- DSA - Dynamic Programming
- DSA - Matrix Chain Multiplication
- DSA - Floyd Warshall Algorithm
- DSA - 0-1 Knapsack Problem
- DSA - Longest Common Sub-sequence Algorithm
- DSA - Travelling Salesman Problem (Dynamic Approach)
- Hashing
- DSA - Hashing Data Structure
- DSA - Collision In Hashing
- Disjoint Set
- DSA - Disjoint Set
- DSA - Path Compression And Union By Rank
- Heap
- DSA - Heap Data Structure
- DSA - Binary Heap
- DSA - Binomial Heap
- DSA - Fibonacci Heap
- Tries Data Structure
- DSA - Tries
- DSA - Standard Tries
- DSA - Compressed Tries
- DSA - Suffix Tries
- Treaps
- DSA - Treaps Data Structure
- Bit Mask
- DSA - Bit Mask In Data Structures
- Bloom Filter
- DSA - Bloom Filter Data Structure
- Approximation Algorithms
- DSA - Approximation Algorithms
- DSA - Vertex Cover Algorithm
- DSA - Set Cover Problem
- DSA - Travelling Salesman Problem (Approximation Approach)
- Randomized Algorithms
- DSA - Randomized Algorithms
- DSA - Randomized Quick Sort Algorithm
- DSA - Karger’s Minimum Cut Algorithm
- DSA - Fisher-Yates Shuffle Algorithm
- Miscellaneous
- DSA - Infix to Postfix
- DSA - Bellmon Ford Shortest Path
- DSA - Maximum Bipartite Matching
- DSA Useful Resources
- DSA - Questions and Answers
- DSA - Selection Sort Interview Questions
- DSA - Merge Sort Interview Questions
- DSA - Insertion Sort Interview Questions
- DSA - Heap Sort Interview Questions
- DSA - Bubble Sort Interview Questions
- DSA - Bucket Sort Interview Questions
- DSA - Radix Sort Interview Questions
- DSA - Cycle Sort Interview Questions
- DSA - Quick Guide
- DSA - Useful Resources
- DSA - Discussion
Binary Search Algorithm
Binary search is a fast search algorithm with run-time complexity of (log n). This search algorithm works on the principle of divide and conquer, since it divides the array into half before searching. For this algorithm to work properly, the data collection should be in the sorted form.
Binary search looks for a particular key value by comparing the middle most item of the collection. If a match occurs, then the index of item is returned. But if the middle item has a value greater than the key value, the right sub-array of the middle item is searched. Otherwise, the left sub-array is searched. This process continues recursively until the size of a subarray reduces to zero.
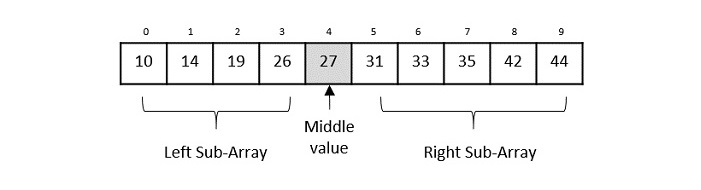
Binary Search Algorithm
Binary Search algorithm is an interval searching method that performs the searching in intervals only. The input taken by the binary search algorithm must always be in a sorted array since it divides the array into subarrays based on the greater or lower values. The algorithm follows the procedure below −
Step 1 − Select the middle item in the array and compare it with the key value to be searched. If it is matched, return the position of the median.
Step 2 − If it does not match the key value, check if the key value is either greater than or less than the median value.
Step 3 − If the key is greater, perform the search in the right sub-array; but if the key is lower than the median value, perform the search in the left sub-array.
Step 4 − Repeat Steps 1, 2 and 3 iteratively, until the size of sub-array becomes 1.
Step 5 − If the key value does not exist in the array, then the algorithm returns an unsuccessful search.
Pseudocode
The pseudocode of binary search algorithms should look like this −
Procedure binary_search
A ← sorted array
n ← size of array
x ← value to be searched
Set lowerBound = 1
Set upperBound = n
while x not found
if upperBound < lowerBound
EXIT: x does not exists.
set midPoint = lowerBound + ( upperBound - lowerBound ) / 2
if A[midPoint] < x
set lowerBound = midPoint + 1
if A[midPoint] > x
set upperBound = midPoint - 1
if A[midPoint] = x
EXIT: x found at location midPoint
end while
end procedure
Analysis
Since the binary search algorithm performs searching iteratively, calculating the time complexity is not as easy as the linear search algorithm.
The input array is searched iteratively by dividing into multiple sub-arrays after every unsuccessful iteration. Therefore, the recurrence relation formed would be of a dividing function.
To explain it in simpler terms,
During the first iteration, the element is searched in the entire array. Therefore, length of the array = n.
In the second iteration, only half of the original array is searched. Hence, length of the array = n/2.
In the third iteration, half of the previous sub-array is searched. Here, length of the array will be = n/4.
Similarly, in the ith iteration, the length of the array will become n/2i
To achieve a successful search, after the last iteration the length of array must be 1. Hence,
n/2i = 1
That gives us −
n = 2i
Applying log on both sides,
log n = log 2i log n = i. log 2 i = log n
The time complexity of the binary search algorithm is O(log n)
Example
For a binary search to work, it is mandatory for the target array to be sorted. We shall learn the process of binary search with a pictorial example. The following is our sorted array and let us assume that we need to search the location of value 31 using binary search.

First, we shall determine half of the array by using this formula −
mid = low + (high - low) / 2
Here it is, 0 + (9 - 0) / 2 = 4 (integer value of 4.5). So, 4 is the mid of the array.

Now we compare the value stored at location 4, with the value being searched, i.e. 31. We find that the value at location 4 is 27, which is not a match. As the value is greater than 27 and we have a sorted array, so we also know that the target value must be in the upper portion of the array.

We change our low to mid + 1 and find the new mid value again.
low = mid + 1 mid = low + (high - low) / 2
Our new mid is 7 now. We compare the value stored at location 7 with our target value 31.
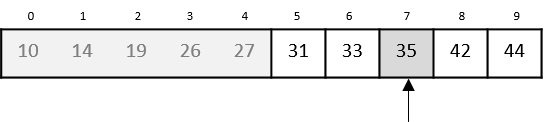
The value stored at location 7 is not a match, rather it is less than what we are looking for. So, the value must be in the lower part from this location.

Hence, we calculate the mid again. This time it is 5.
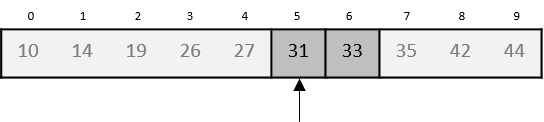
We compare the value stored at location 5 with our target value. We find that it is a match.

We conclude that the target value 31 is stored at location 5.
Binary search halves the searchable items and thus reduces the count of comparisons to be made to very less numbers.
Implementation
Binary search is a fast search algorithm with run-time complexity of (log n). This search algorithm works on the principle of divide and conquer. For this algorithm to work properly, the data collection should be in a sorted form.
#include<stdio.h>
void binary_search(int a[], int low, int high, int key){
int mid;
mid = (low + high) / 2;
if (low <= high) {
if (a[mid] == key)
printf("Element found at index: %d\n", mid);
else if(key < a[mid])
binary_search(a, low, mid-1, key);
else if (a[mid] < key)
binary_search(a, mid+1, high, key);
} else if (low > high)
printf("Unsuccessful Search\n");
}
int main(){
int i, n, low, high, key;
n = 5;
low = 0;
high = n-1;
int a[10] = {12, 14, 18, 22, 39};
key = 22;
binary_search(a, low, high, key);
key = 23;
binary_search(a, low, high, key);
return 0;
}
Output
Element found at index: 3 Unsuccessful Search
#include <iostream>
using namespace std;
void binary_search(int a[], int low, int high, int key){
int mid;
mid = (low + high) / 2;
if (low <= high) {
if (a[mid] == key)
cout << "Element found at index: " << mid << endl;
else if(key < a[mid])
binary_search(a, low, mid-1, key);
else if (a[mid] < key)
binary_search(a, mid+1, high, key);
} else if (low > high)
cout << "Unsuccessful Search" <<endl;
}
int main(){
int i, n, low, high, key;
n = 5;
low = 0;
high = n-1;
int a[10] = {12, 14, 18, 22, 39};
key = 22;
binary_search(a, low, high, key);
key = 23;
binary_search(a, low, high, key);
return 0;
}
Output
Element found at index: 3 Unsuccessful Search
import java.io.*;
import java.util.*;
public class BinarySearch {
static void binary_search(int a[], int low, int high, int key) {
int mid = (low + high) / 2;
if (low <= high) {
if (a[mid] == key)
System.out.println("Element found at index: " + mid);
else if(key < a[mid])
binary_search(a, low, mid-1, key);
else if (a[mid] < key)
binary_search(a, mid+1, high, key);
} else if (low > high)
System.out.println("Unsuccessful Search");
}
public static void main(String args[]) {
int n, key, low, high;
n = 5;
low = 0;
high = n-1;
int a[] = {12, 14, 18, 22, 39};
key = 22;
binary_search(a, low, high, key);
key = 23;
binary_search(a, low, high, key);
}
}
Output
Element found at index: 3 Unsuccessful Search
def binary_search(a, low, high, key):
mid = (low + high) // 2
if (low <= high):
if(a[mid] == key):
print("The element is present at index:", mid)
elif(key < a[mid]):
binary_search(a, low, mid-1, key)
elif (a[mid] < key):
binary_search(a, mid+1, high, key)
if(low > high):
print("Unsuccessful Search")
a = [6, 12, 14, 18, 22, 39, 55, 182]
n = len(a)
low = 0
high = n-1
key = 22
binary_search(a, low, high, key)
key = 54
binary_search(a, low, high, key)
Output
The element is present at index: 4 Unsuccessful Search
