Aho-Corasick Algorithm

Aho-Corasick Algorithm for Pattern Matching

The Aho-Corasick algorithm is a dictionary-matching algorithm that can find all the occurrences of all sets of patterns within a given text in linear time. It was developed by Alfred V. Aho and Margaret J. Corasick in 1975 and is widely used in applications such as malware detection, text analysis, and natural language processing.

How does Aho-Corasick Algorithm work?

The Aho-Corasick algorithm requires only one pass over the text to search for all patterns and it does not do any unnecessary backtracking. It can handle multiple keywords of different lengths, and it can also handle overlapping matches with ease.

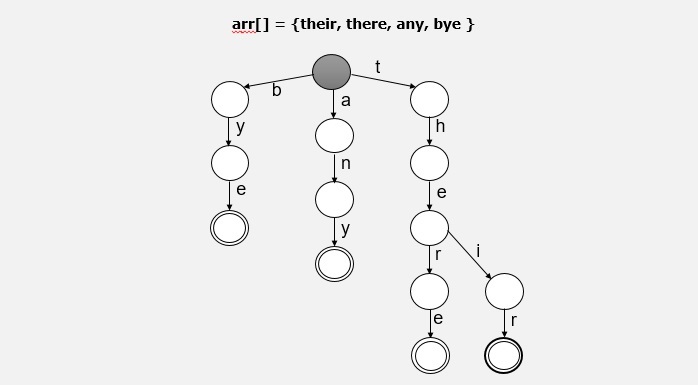
This algorithm keeps track of searched patterns with the help of a trie data structure. A trie is a tree-based data structure mainly used for storing strings.

let's understand with an example −

Input:
set of patterns = {their, there, any, bye} 
main string = "isthereanyanswerokgoodbye"
Output:
Word there location: 2
Word any location: 7
Word bye location: 22
Pattern Aho-Corasick

The Aho-Corasick algorithm consists of the following steps −

  • Preprocessing
  • Searching/Matching

Preprocessing Stage

In the preprocessing step, we construct the finite-state machine(trie) from the keywords. The trie has a node for each prefix of the keywords, and an edge labelled with a character for each possible extension of the prefix. The root node of trie represents the empty prefix, and the last node is marked as final.

The preprocessing step is further divided into three sub-steps −

  • Go-to Stage − This stage defines the transitions between the states based on the characters of the patterns. It is represented as a two-dimensional array.

  • Failure Stage − It defines the transitions between the states when a mismatch occurs. It is represented as a one-dimensional array.

  • Output Stage − At this stage, the algorithm stores the indexes of all the patterns that end at a given state. It is also represented by a one-dimensional array.

Searching/Matching Stage

The searching step is done by scanning the text from left to right, and following the edges and failure links in the trie according to the characters in the text. Whenever we reach the final node, we report a match of the corresponding keyword in the text.

Example

The following example demonstrates the working of Aho-Corasick algorithm in different programming languages.

C C++ Java Python 
#include <stdio.h>
#include <string.h>
#define MAXS 500    // sum of the length of all patterns
#define MAXC 26     // as 26 letters in alphabet
int output[MAXS];
int fail[MAXS];
int gotoMat[MAXS][MAXC];
int buildTree(char* array[], int size) {
   for(int i = 0; i<MAXS; i++)
      output[i] = 0;  // all element of output array is 0
   for(int i = 0; i<MAXS; i++)
      fail[i] = -1;  // all element of failure array is -1
   for(int i = 0; i<MAXS; i++)
      for(int j = 0; j<MAXC; j++)
         gotoMat[i][j] = -1;  // all element of goto matrix is -1
   // initial state
   int state = 1;    
   // make trie for all pattern in array
   for (int i = 0; i < size; i++) {    
      char* word = array[i];
      int presentState = 0;
      // adding pattern
      for (int j = 0; j < strlen(word); ++j) {    
         int ch = word[j] - 'a';
         if (gotoMat[presentState][ch] == -1)    
            // increasing state
            gotoMat[presentState][ch] = state++;   
         presentState = gotoMat[presentState][ch];
      }
      // adding current word in the output
      output[presentState] |= (1 << i); 
   }
   // if ch is not directly connected to root node
   for (int ch = 0; ch < MAXC; ++ch)   
      if (gotoMat[0][ch] == -1)
         gotoMat[0][ch] = 0;
   // node goes to previous state when fails
   for (int ch = 0; ch < MAXC; ++ch) {    
      if (gotoMat[0][ch] != 0) {
         fail[gotoMat[0][ch]] = 0;
         // adding next level node to the queue
         int q[MAXS], front = 0, rear = 0;
         q[rear++] = gotoMat[0][ch];
         while (front != rear) {
            // removing front node
            int state = q[front++];   
            for (int ch = 0; ch <= MAXC; ++ch) {
               // if goto state is present
               if (gotoMat[state][ch] != -1) {    
                  int failure = fail[state];
                  // find deepest node with proper suffix
                  while (gotoMat[failure][ch] == -1)    
                     failure = fail[failure];
                  failure = gotoMat[failure][ch];
                  fail[gotoMat[state][ch]] = failure;
                  // Merging output values
                  output[gotoMat[state][ch]] |= output[failure];  
                  // adding next level node to the queue
                  q[rear++] = gotoMat[state][ch];    
               }
            }
         }
      }
   }
   return state;
}
int getNextState(int presentState, char nextChar) {
   int answer = presentState;
   int ch = nextChar - 'a'; //subtract ascii of 'a'
   // if go to is not found, use failure function
   while (gotoMat[answer][ch] == -1) 
      answer = fail[answer];
   return gotoMat[answer][ch];
}
void patternSearch(char* arr[], int size, char* text) {
   buildTree(arr, size);  // make the trie structure
   int presentState = 0;  // make current state as 0
   // to find all occurances of pattern
   for (int i = 0; i < strlen(text); i++) {    
      presentState = getNextState(presentState, text[i]);
      // matching found and print words
      for (int j = 0; j < size; ++j) {  
         if (output[presentState] & (1 << j)) {
           printf("Word %s location: %zu\n", arr[j], i - strlen(arr[j]) + 1);
         }
      }
   }
}
int main() {
   char* arr[] = {"their", "there", "answer", "any", "bye"};
   char* text = "isthereanyanswerokgoodbye";
   int k = sizeof(arr)/sizeof(arr[0]);
   patternSearch(arr, k, text);
   return 0;
}

#include <iostream>
#include <queue>
#define MAXS 500    // sum of the length of all patterns
#define MAXC 26     // as 26 letters in alphabet
using namespace std;
int output[MAXS];
int fail[MAXS];
int gotoMat[MAXS][MAXC];
int buildTree(string array[], int size) {
   for(int i = 0; i<MAXS; i++)
      output[i] = 0;  // all element of output array is 0
   for(int i = 0; i<MAXS; i++)
      fail[i] = -1;  // all element of failure array is -1
   for(int i = 0; i<MAXS; i++)
      for(int j = 0; j<MAXC; j++)
         gotoMat[i][j] = -1;  // all element of goto matrix is -1
   // initial state
   int state = 1;    
   // make trie for all pattern in array
   for (int i = 0; i < size; i++) {    
      string word = array[i];
      int presentState = 0;
      // adding pattern
      for (int j = 0; j < word.size(); ++j) {    
         int ch = word[j] - 'a';
         if (gotoMat[presentState][ch] == -1)    
            // increasing state
            gotoMat[presentState][ch] = state++;   
         presentState = gotoMat[presentState][ch];
      }
      // adding current word in the output
      output[presentState] |= (1 << i); 
   }
   // if ch is not directly connected to root node
   for (int ch = 0; ch < MAXC; ++ch)   
      if (gotoMat[0][ch] == -1)
         gotoMat[0][ch] = 0;
   queue<int> q;
   // node goes to previous state when fails
   for (int ch = 0; ch < MAXC; ++ch) {    
      if (gotoMat[0][ch] != 0) {
         fail[gotoMat[0][ch]] = 0;
         q.push(gotoMat[0][ch]);
      }
   }
   while (q.size()) {
      // removing front node
      int state = q.front();   
      q.pop();
      for (int ch = 0; ch <= MAXC; ++ch) {
         // if goto state is present
         if (gotoMat[state][ch] != -1) {    
            int failure = fail[state];
            // find deepest node with proper suffix
            while (gotoMat[failure][ch] == -1)    
               failure = fail[failure];
               failure = gotoMat[failure][ch];
               fail[gotoMat[state][ch]] = failure;
               // Merging output values
               output[gotoMat[state][ch]] |= output[failure];  
               // adding next level node to the queue
               q.push(gotoMat[state][ch]);    
         }
      }
   }
   return state;
}
int getNextState(int presentState, char nextChar) {
   int answer = presentState;
   int ch = nextChar - 'a'; //subtract ascii of 'a'
   // if go to is not found, use failure function
   while (gotoMat[answer][ch] == -1) 
      answer = fail[answer];
   return gotoMat[answer][ch];
}
void patternSearch(string arr[], int size, string text) {
   buildTree(arr, size);  // make the trie structure
   int presentState = 0;  // make current state as 0
   // to find all occurances of pattern
   for (int i = 0; i < text.size(); i++) {    
      presentState = getNextState(presentState, text[i]);
      // matching found and print words
      for (int j = 0; j < size; ++j) {  
         if (output[presentState] & (1 << j)) {
            cout << "Word " << arr[j] << " location: " << i - arr[j].size() + 1 << endl;
         }
      }
   }
}
int main() {
   string arr[] = {"their", "there", "answer", "any", "bye"};
   string text = "isthereanyanswerokgoodbye";
   int k = sizeof(arr)/sizeof(arr[0]);
   patternSearch(arr, k, text);
   return 0;
}

import java.util.*;
public class Main {
   static final int MAXS = 500; // sum of the length of all patterns
   static final int MAXC = 26;  // as 26 letters in alphabet
   static int[] output = new int[MAXS];
   static int[] fail = new int[MAXS];
   static int[][] gotoMat = new int[MAXS][MAXC];
   // method to construct trie
   static int buildTree(String[] array, int size) {
      for(int i = 0; i<MAXS; i++)
         output[i] = 0;  // all element of output array is 0
      for(int i = 0; i<MAXS; i++)
         fail[i] = -1;  // all element of failure array is -1
      for(int i = 0; i<MAXS; i++)
         for(int j = 0; j<MAXC; j++)
            gotoMat[i][j] = -1;  // all element of goto matrix is -1
        // initial state
        int state = 1;    
        // make trie for all pattern in array
        for (int i = 0; i < size; i++) {    
            String word = array[i];
            int presentState = 0;
            // adding pattern
            for (int j = 0; j < word.length(); ++j) {    
                int ch = word.charAt(j) - 'a';
                if (gotoMat[presentState][ch] == -1)    
                    // increasing state
                    gotoMat[presentState][ch] = state++;   
                presentState = gotoMat[presentState][ch];
            }
            // adding current word in the output
            output[presentState] |= (1 << i); 
        }
        // if ch is not directly connected to root node
        for (int ch = 0; ch < MAXC; ++ch)   
            if (gotoMat[0][ch] == -1)
                gotoMat[0][ch] = 0;
        Queue<Integer> q = new LinkedList<>();
        // node goes to previous state when fails
        for (int ch = 0; ch < MAXC; ++ch) {    
            if (gotoMat[0][ch] != 0) {
                fail[gotoMat[0][ch]] = 0;
                q.add(gotoMat[0][ch]);
            }
        }
        while (!q.isEmpty()) {
            // removing front node
            state = q.poll();   
            for (int ch = 0; ch < MAXC; ++ch) {
                // if goto state is present
                if (gotoMat[state][ch] != -1) {    
                    int failure = fail[state];
                    // find deepest node with proper suffix
                    while (gotoMat[failure][ch] == -1)    
                        failure = fail[failure];
                    failure = gotoMat[failure][ch];
                    fail[gotoMat[state][ch]] = failure;
                    // Merging output values
                    output[gotoMat[state][ch]] |= output[failure];  
                    // adding next level node to the queue
                    q.add(gotoMat[state][ch]);    
                }
            }
        }
        return state;
    }
    static int getNextState(int presentState, char nextChar) {
        int answer = presentState;
        int ch = nextChar - 'a'; //subtract ascii of 'a'
        // if go to is not found, use failure function
        while (gotoMat[answer][ch] == -1) 
            answer = fail[answer];
        return gotoMat[answer][ch];
    }
    static void patternSearch(String[] arr, int size, String text) {
        buildTree(arr, size);  // make the trie structure
        int presentState = 0;  // make current state as 0
        // to find all occurances of pattern
        for (int i = 0; i < text.length(); i++) {    
            presentState = getNextState(presentState, text.charAt(i));
            // matching found and print words
            for (int j = 0; j < size; ++j) {  
                if ((output[presentState] & (1 << j)) != 0) {
                    System.out.println("Word " + arr[j] + " location: " + (i - arr[j].length() + 1));
                }
            }
        }
    }
    public static void main(String[] args) {
        String[] arr = {"their", "there", "answer", "any", "bye"};
        String text = "isthereanyanswerokgoodbye";
        int k = arr.length;
        patternSearch(arr, k, text);
    }
}

from collections import deque
MAXS = 500    # sum of the length of all patterns
MAXC = 26     # as 26 letters in alphabet
output = [0]*MAXS
fail = [-1]*MAXS
gotoMat = [[-1]*MAXC for _ in range(MAXS)]
# function to construct trie
def buildTree(array):
    global output, fail, gotoMat
    size = len(array)
    # initial state
    state = 1    
    # make trie for all pattern in array
    for i in range(size):    
        word = array[i]
        presentState = 0
        # adding pattern
        for j in range(len(word)):    
            ch = ord(word[j]) - ord('a')
            if gotoMat[presentState][ch] == -1:    
                # increasing state
                gotoMat[presentState][ch] = state   
                state += 1
            presentState = gotoMat[presentState][ch]
        # adding current word in the output
        output[presentState] |= (1 << i) 
    # if ch is not directly connected to root node
    for ch in range(MAXC):   
        if gotoMat[0][ch] == -1:
            gotoMat[0][ch] = 0
    q = deque()
    # node goes to previous state when fails
    for ch in range(MAXC):    
        if gotoMat[0][ch] != 0:
            fail[gotoMat[0][ch]] = 0
            q.append(gotoMat[0][ch])
    while q:
        # removing front node
        state = q.popleft()   
        for ch in range(MAXC):
            # if goto state is present
            if gotoMat[state][ch] != -1:    
                failure = fail[state]
                # find deepest node with proper suffix
                while gotoMat[failure][ch] == -1:    
                    failure = fail[failure]
                failure = gotoMat[failure][ch]
                fail[gotoMat[state][ch]] = failure
                # Merging output values
                output[gotoMat[state][ch]] |= output[failure]  
                # adding next level node to the queue
                q.append(gotoMat[state][ch])    
    return state

def getNextState(presentState, nextChar):
    answer = presentState
    ch = ord(nextChar) - ord('a') #subtract ascii of 'a'
    # if go to is not found, use failure function
    while gotoMat[answer][ch] == -1: 
        answer = fail[answer]
    return gotoMat[answer][ch]

def patternSearch(arr, text):
    buildTree(arr)  # make the trie structure
    presentState = 0  # make current state as 0
    size = len(arr)
    # to find all occurances of pattern
    for i in range(len(text)):    
        presentState = getNextState(presentState, text[i])
        # matching found and print words
        for j in range(size):  
            if (output[presentState] & (1 << j)) != 0:
                print(f"Word {arr[j]} location: {i - len(arr[j]) + 1}")

def main():
    arr = ["their", "there", "answer", "any", "bye"]
    text = "isthereanyanswerokgoodbye"
    patternSearch(arr, text)

if __name__ == "__main__":
    main()

Output

Word there location: 2
Word any location: 7
Word answer location: 10
Word bye location: 22
Advertisements