
- Computer Organization Tutorial
- CO - Home
- CO - Overview
- CO - Digital Number System
- CO - Number System Conversion
- CO - Binary Codes
- CO - Codes Conversion
- CO - Complement Arithmetic
- CO - Binary Arithmetic
- CO - Octal Arithmetic
- CO - Hexadecimal Arithmetic
- CO - Boolean Algebra
- CO - Logic Gates
- CO - Combinational Circuits
- CO - Sequential Circuits
- CO - Digital Registers
- CO - Digital Counters
- CO - Memory Devices
- CO - CPU Architecture
- Computer Organization Resources
- CO - Quick Guide
- CO - Useful Resources
- CO - Discussion
Boolean Algebra
Boolean Algebra is used to analyze and simplify the digital (logic) circuits. It uses only the binary numbers i.e. 0 and 1. It is also called as Binary Algebra or logical Algebra. Boolean algebra was invented by George Boole in 1854.
Rule in Boolean Algebra
Following are the important rules used in Boolean algebra.
Variable used can have only two values. Binary 1 for HIGH and Binary 0 for LOW.
Complement of a variable is represented by an overbar (-). Thus, complement of variable B is represented as
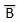 . Thus if B = 0 then
. Thus if B = 0 then 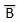 = 1 and B = 1 then
= 1 and B = 1 then 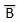 = 0.
= 0.ORing of the variables is represented by a plus (+) sign between them. For example ORing of A, B, C is represented as A + B + C.
Logical ANDing of the two or more variable is represented by writing a dot between them such as A.B.C. Sometime the dot may be omitted like ABC.
Boolean Laws
There are six types of Boolean Laws.
Commutative law
Any binary operation which satisfies the following expression is referred to as commutative operation.

Commutative law states that changing the sequence of the variables does not have any effect on the output of a logic circuit.
Associative law
This law states that the order in which the logic operations are performed is irrelevant as their effect is the same.
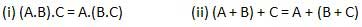
Distributive law
Distributive law states the following condition.
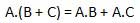
AND law
These laws use the AND operation. Therefore they are called as AND laws.
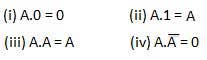
OR law
These laws use the OR operation. Therefore they are called as OR laws.
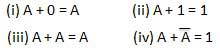
INVERSION law
This law uses the NOT operation. The inversion law states that double inversion of a variable results in the original variable itself.
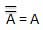
Important Boolean Theorems
Following are few important boolean Theorems.
| Boolean function/theorems | Description |
|---|---|
| Boolean Functions and Expressions, K-Map and NAND Gates realization | |
| De Morgan's Theorem 1 and Theorem 2 |