
- Computer Organization Tutorial
- CO - Home
- CO - Overview
- CO - Digital Number System
- CO - Number System Conversion
- CO - Binary Codes
- CO - Codes Conversion
- CO - Complement Arithmetic
- CO - Binary Arithmetic
- CO - Octal Arithmetic
- CO - Hexadecimal Arithmetic
- CO - Boolean Algebra
- CO - Logic Gates
- CO - Combinational Circuits
- CO - Sequential Circuits
- CO - Digital Registers
- CO - Digital Counters
- CO - Memory Devices
- CO - CPU Architecture
- Computer Organization Resources
- CO - Quick Guide
- CO - Useful Resources
- CO - Discussion
Complement Arithmetic
Complements are used in the digital computers in order to simplify the subtraction operation and for the logical manipulations. For each radix-r system (radix r represents base of number system) there are two types of complements.
| S.N. | Complement | Description |
|---|---|---|
| 1 | Radix Complement | The radix complement is referred to as the r's complement |
| 2 | Diminished Radix Complement | The diminished radix complement is referred to as the (r-1)'s complement |
Binary system complements
As the binary system has base r = 2. So the two types of complements for the binary system are 2's complement and 1's complement.
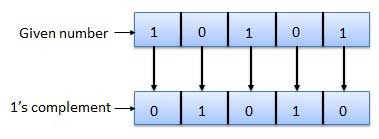
1's complement
The 1's complement of a number is found by changing all 1's to 0's and all 0's to 1's. This is called as taking complement or 1's complement. Example of 1's Complement is as follows.
2's complement
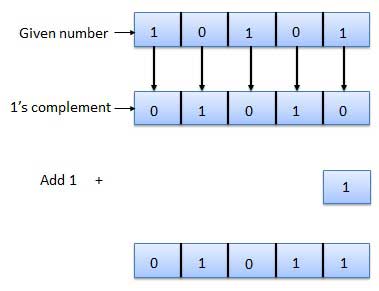
The 2's complement of binary number is obtained by adding 1 to the Least Significant Bit (LSB) of 1's complement of the number.
2's complement = 1's complement + 1
Example of 2's Complement is as follows.
Advertisements