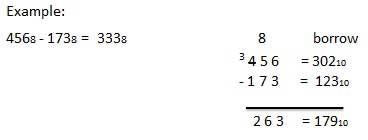- Computer Organization Tutorial
- CO - Home
- CO - Overview
- CO - Digital Number System
- CO - Number System Conversion
- CO - Binary Codes
- CO - Codes Conversion
- CO - Complement Arithmetic
- CO - Binary Arithmetic
- CO - Octal Arithmetic
- CO - Hexadecimal Arithmetic
- CO - Boolean Algebra
- CO - Logic Gates
- CO - Combinational Circuits
- CO - Sequential Circuits
- CO - Digital Registers
- CO - Digital Counters
- CO - Memory Devices
- CO - CPU Architecture
- Computer Organization Resources
- CO - Quick Guide
- CO - Useful Resources
- CO - Discussion
Octal Arithmetic
Octal Number System
Following are the characteristics of an octal number system.
Uses eight digits, 0,1,2,3,4,5,6,7.
Also called base 8 number system.
Each position in an octal number represents a 0 power of the base (8). Example: 80
Last position in an octal number represents an x power of the base (8). Example: 8x where x represents the last position - 1.
Example
Octal Number − 125708
Calculating Decimal Equivalent −
| Step | Octal Number | Decimal Number |
|---|---|---|
| Step 1 | 125708 | ((1 × 84) + (2 × 83) + (5 × 82) + (7 × 81) + (0 × 80))10 |
| Step 2 | 125708 | (4096 + 1024 + 320 + 56 + 0)10 |
| Step 3 | 125708 | 549610 |
Note − 125708 is normally written as 12570.
Octal Addition
Following octal addition table will help you to handle octal addition.

To use this table, simply follow the directions used in this example: Add 68 and 58. Locate 6 in the A column then locate the 5 in the B column. The point in 'sum' area where these two columns intersect is the 'sum' of two numbers.
68 + 58 = 138.
Example − Addition
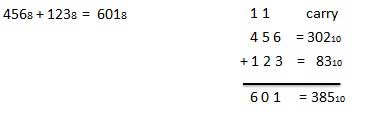
Octal Subtraction
The subtraction of octal numbers follows the same rules as the subtraction of numbers in any other number system. The only variation is in borrowed number. In the decimal system, you borrow a group of 1010. In the binary system, you borrow a group of 210. In the octal system you borrow a group of 810.
Example − Subtraction