- Time Series Tutorial
- Time Series - Home
- Time Series - Introduction
- Time Series - Programming Languages
- Time Series - Python Libraries
- Data Processing & Visualization
- Time Series - Modeling
- Time Series - Parameter Calibration
- Time Series - Naive Methods
- Time Series - Auto Regression
- Time Series - Moving Average
- Time Series - ARIMA
- Time Series - Variations of ARIMA
- Time Series - Exponential Smoothing
- Time Series - Walk Forward Validation
- Time Series - Prophet Model
- Time Series - LSTM Model
- Time Series - Error Metrics
- Time Series - Applications
- Time Series - Further Scope
- Time Series Useful Resources
- Time Series - Quick Guide
- Time Series - Useful Resources
- Time Series - Discussion
Time Series - Moving Average
For a stationary time series, a moving average model sees the value of a variable at time ‘t’ as a linear function of residual errors from ‘q’ time steps preceding it. The residual error is calculated by comparing the value at the time ‘t’ to moving average of the values preceding.
Mathematically it can be written as −
$$y_{t} = c\:+\:\epsilon_{t}\:+\:\theta_{1}\:\epsilon_{t-1}\:+\:\theta_{2}\:\epsilon_{t-2}\:+\:...+:\theta_{q}\:\epsilon_{t-q}\:$$
Where‘q’ is the moving-average trend parameter
$\epsilon_{t}$ is white noise, and
$\epsilon_{t-1}, \epsilon_{t-2}...\epsilon_{t-q}$ are the error terms at previous time periods.
Value of ‘q’ can be calibrated using various methods. One way of finding the apt value of ‘q’ is plotting the partial auto-correlation plot.
A partial auto-correlation plot shows the relation of a variable with itself at prior time steps with indirect correlations removed, unlike auto-correlation plot which shows direct as well as indirect correlations, let’s see how it looks like for ‘temperature’ variable of our data.
Showing PACP
In [143]:
from statsmodels.graphics.tsaplots import plot_pacf plot_pacf(train, lags = 100) plt.show()
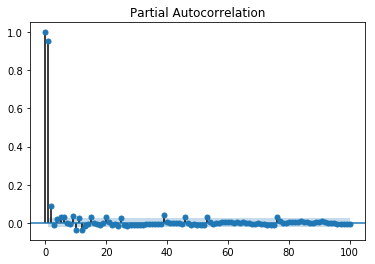
A partial auto-correlation is read in the same way as a correlogram.
To Continue Learning Please Login