Show that the whole compilation process for statement A = B * C + 20, where A, B, C are of real types

Solution

                    Symbol Table

Now, we will see how we can perform the compiler phase at each level and how it works.

• Lexical Analysis

This is the first step that works as an integration between the compiler and the source language code. It reads the source code one character at a time and designs a source code into a series of atomic units known as tokens.

In this phase, we will see how we can tokenize the expression.

A → Identifier: (id, 1)

= → Operator: Assignment

B → Identifier: (id, 2)

* → Operator: Multiplication

C → Identifier: (id, 3)

+ → Operator: Binary Addition

20 → Constant: Integer

The final expression is as follows −

id1=id2*id3+20

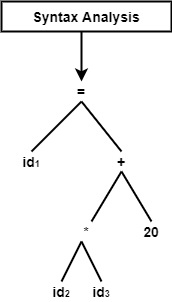
• Syntax Analysis

It is also known as the parser. It receives tokens as its input generated from the previous phase (lexical analysis) and produces a hierarchical structure called syntax tree or parse tree.

In this phase, it can check the syntax after tokenized the expression.

Syntax Analysis for the expression is as follows −

• Semantic Analysis

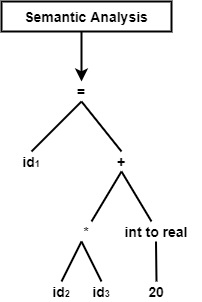
This phase makes the syntax tree input and determines the semantical accuracy of the program. However, the tokens are accurate and syntactically right; they may be precise, not semantically. Hence the semantic analyzer determines the semantics (meaning) of the statements construct. In this phase, it can verify the type and semantic action for the syntax tree.

• Intermediate Code Generation

This phase takes the syntactically and semantically correct form as input and produces the same intermediate notation of the source code. In this phase, we will provide a changed parse tree and as output after transforming into the Intermediate program will create a three-address code.

T1=id2 * id3
T2=int to real (20)
T3=T1+T2
id1=T3

• Code Optimization

It is an optional phase. It converts the intermediate representation of the source program into an efficient code. In this phase, it would look as an input will provide three address code and as an output, and it will identify the optimized code.

T1=id2 * id3
id1=T1+ 20.0

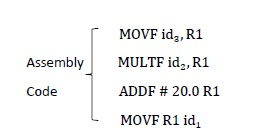
• Code Generation

This is the final step of the compilation process. It converts optimized intermediate code into Machine/Assembly code. It allocates memory locations for variables in the program.

In the last phase, it can see how can modify the final expression into the assembly program.

Ginni

Published on 22-Oct-2021 11:50:35

• Related Questions & Answers
• Show that the following grammar is LR (1)\nS → A a |b A c |B c | b B a\nA → d\nB → d
• Larger of a^b or b^a in C++
• Count number of pairs (A <= N, B <= N) such that gcd (A , B) is B in C++
• Count number of triplets (a, b, c) such that a^2 + b^2 = c^2 and 1<=a<=b<=c<= n in C++
• Find a palindromic string B such that given String A is a subsequence of B in C++
• Construct Quadruples, Triples, and Indirect Triples for the expression\n-(a + b) * (c + d) - (a + b + c)
• Find FIRST & FOLLOW for the following Grammar.\nS → A a A | B b B\nA → b B\nB → ε
• Find all pairs (a, b) in an array such that a % b = k in C++
• Construct a Finite Automata for the regular expression ((a+b)(a+b))*.
• Find four elements a, b, c and d in an array such that a+b = c+d in C++
• Program to find N-th term of series a, b, b, c, c, c…in C++
• Find Last Digit of a^b for Large Numbers in C++
• Find (a^b)%m where ‘a’ is very large in C++
• Find numbers a and b that satisfy the given condition in C++
• Number of Digits in a^b in C++