Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Resistors in AC Circuits
Important Terms
AC Circuit − A closed path followed by alternating current is called as an AC Circuit.
Resistance − The measure of opposition offered by a material in the path of electric current is known as resistance of that material. The element possessing the resistance is known as Resistor.
Peak Value of Voltage or Current − It is the maximum value attained by an alternating quantity. It is also called as Amplitude.
Average Value − The arithmetical average of all values of an alternating quantity over one cycle is called as average value. For sinusoidal voltage or current,
$$\mathrm{I_{avg}=\frac{2I_{m}}{\pi}=0.637I_{m}}$$
$$\mathrm{V_{avg}=\frac{2V_{m}}{\pi}=0.637I_{m}}$$
Root Mean Square (RMS) value − The RMS value of an alternating current is that value of DC current when flowing through a given resistance for a given time produces the same amount of heat as when produced by the alternating current when flowing through the same resistance for the same time. The RMS value of sinusoidal current and voltage is,
$$\mathrm{I_{RMS}=\frac{I_{m}}{\sqrt{2}}=0.707I_{m}}$$
$$\mathrm{V_{RMS}=\frac{V_{m}}{\sqrt{2}}=0.707V_{m}}$$
Instantaneous Power (p) − It is the product of the instantaneous voltage (v) across the resistance and the instantaneous current (i) through the resistance.
The instantaneous value of power may be positive or negative. A positive value means power flows from source to load. A negative value means that power flows from load to source.
$$\mathrm{Instantaneous\:Power \:(p)=\upsilon i=\frac{V_{m}I_{m}}{2}-\frac{V_{m}I_{m}}{2}cos(2 \omega t)\:\:\:(wats)}$$
Average Power (P) − The average power is the average of the instantaneous power over one cycle.
$\mathrm{Average\:Power\:(p)=average \:of\:(p=
u i)\:over\:one\:cycle=\frac{V_{m}I_{m}}{2}=VI\:\:(wats)}$
$$\mathrm{V=RMS\:value\:of\:applied \:voltage}$$
$$\mathrm{I=RMS\:value\:of\:circuit\:current}$$
AC Circuit Containing Resistance
Consider a circuit containing a pure resistance of R Ω Omegaconnected across an alternating voltage source.
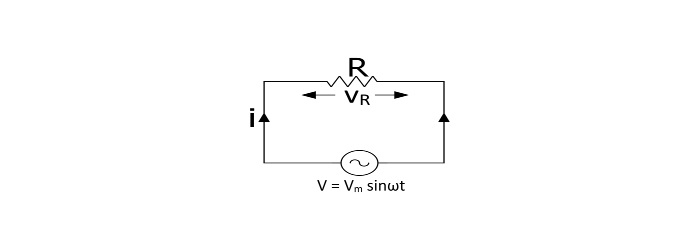
Let the alternating voltage is given by the equation,
$$\mathrm{
u=V_{m}sin\:\omega t} ...(1)$$
Due to this voltage, an alternating current i will flow in the circuit. The total applied voltage appears across the resistance only. Hence,
$$\mathrm{
u=iR}$$
$$\mathrm{i=\frac{
u}{R}=\frac {v_{m}\:sin\:\omega t }{R}=I_{m}\:sin\:\omega t.....(2)}$$
$$Where,\mathrm{I_{m}=\frac{V_{m}}{R}=maximum\:value\:of\:circuit\:circuit}$$
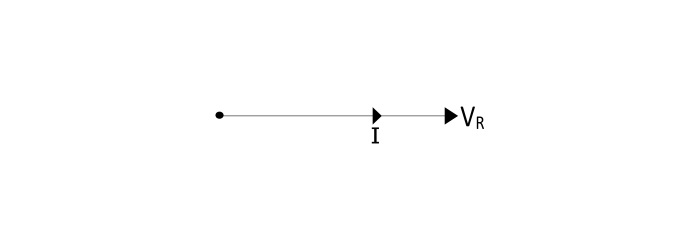
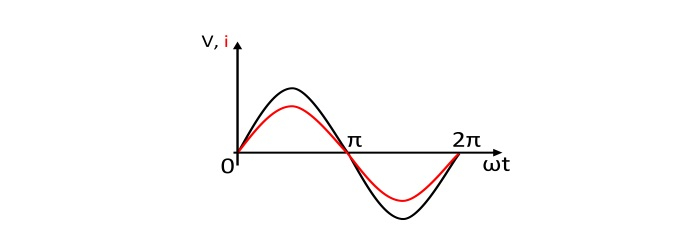
From the equation (1) and (2), it can be seen that, the current through a pure resistor is in phase with voltage across the resistor.
Power in Resistive Circuit
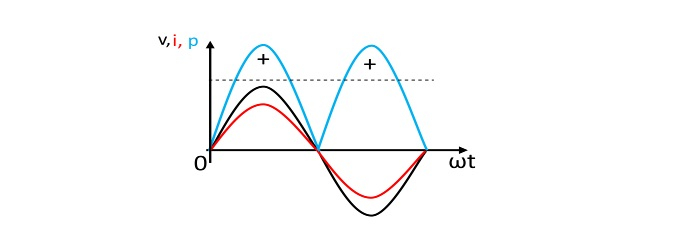
- Instantaneous power
$$\mathrm{p=
u i=\frac{V_{m}I_{m}}{2}-\frac{V_{m}I_{m}}{2}cos(2 \omega t)}$$
The instantaneous power consists of two parts viz. a constant part (VmIm/2) and a fluctuating part (VmIm/2)cos 2ωt.
- Average power
$$\mathrm{Average\:Power\:(p)=average \:of(p=
u i)\:over\:one\:cycle=\frac{V_{m}I_{m}}{2}=VI}$$
Phasor and Wave Diagram
- Phasor Diagram
- Current and Voltage Wave Diagram
- Power Curve
Numerical Example
An AC circuit consists of a pure resistance of 20 Ω and is connected across an AC supply of 240 V, 50 Hz. Calculated (i) circuit current (ii) power consumed by the resistance and (iii) equation for the voltage and current.
Solution
- Circuit Current
$$\mathrm{I=\frac{V}{R}=\frac{240}{20}=12A}$$
- Power Consumed in the circuit
$$\mathrm{P=VI=240×12=2880\:W}$$
- Equation for the voltage and current
$$\mathrm{V_{m}=\sqrt{2}V=\sqrt{2}×240=339.36\:V}$$
$$\mathrm{I_{m}=\sqrt{2}I=\sqrt{2}×12=16.97 A}$$
$$\mathrm{\omega=2\pi f=2\pi×50=314\:rad/sec}$$
Hence,
$$\mathrm{
u=339.36sin(314t)\:\:\:V}$$
$$\mathrm{i=16.97sin(314t)\:\:\:A}$$
883 Views
