Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Power Triangle and Power Factor in AC Circuits
Power in AC circuit
Active Power (P)
The product of voltage (RMS) and current (RMS) with the cosine of the angle between them, in an AC circuit is termed as active power. It is measured in watts (W). For a pure inductive and pure capacitive circuit, the active power being zero.
Active Power,
P = VI cos φ
Reactive Power (Q)
The product of voltage (RMS) and current (RMS) with sine of the angle between them, in an AC circuit is known as reactive power. It is measured in VAR (Volt-Ampere Reactive).
Reactive Power,
Q = VI sin φ
Apparent Power (S)
The product of voltage (RMS) and current (RMS) is called as the apparent power. It is measured in VA (Volt-Ampere).
Apparent Power
S = VI
Power Triangle
The power triangle is the geometrical representation of the apparent power (S), active power (P) and reactive power (Q) in an AC circuit.
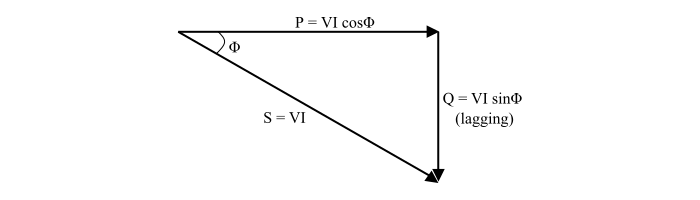
Case 1 – Inductive Circuit
In an inductive circuit, the current lags behind the voltage. Therefore, the reactive power lags behind the active power i.e. an inductor absorbs lagging reactive power and delivers leading reactive power. Hence, the power triangle for a Inductive circuit,
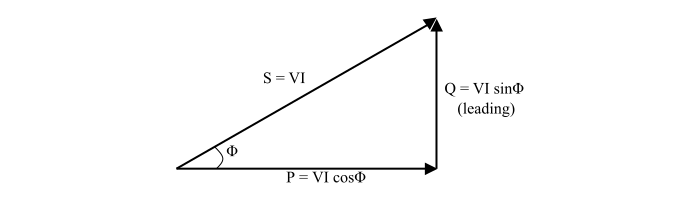
Case 2 – Capacitive Circuit
In a capacitive circuit, the circuit current leads the voltage across the capacitor. Therefore, the reactive power leads ahead of active power i.e. a capacitor absorbs leading reactive power whereas delivers lagging reactive power. Hence, the power triangle for a capacitive circuit,
Power Factor in AC circuit
The power factor of an AC circuit can be defined as the ratio of the active power to the apparent power (total power), i.e.,
$$\mathrm{Power\:Factor=\frac{Active\:Power}{Apparent\:Power}}$$
$$\mathrm{\Rightarrow\:PF=\frac{VI\:\cos\varphi}{VI}=\cos\varphi}$$
Hence, the power factor of an AC circuit is the cosine of phase angle between the voltage and current. It should be noted that, the phase angle (Φ) is the angle between the phase voltage and phase current, not between the line voltage and line current.
1K+ Views
