Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Linear and Nonlinear Resistors
A resistor is a circuit element that opposes the flow of electric current in the circuit by virtue of its property called resistance.
According to I-V characteristic, the resistors may be classified in two categories viz.
- Linear Resistor
- Non-Linear Resistor
Ohm’s Law
If the physical conditions are constant, then the ratio of applied voltage across a conductor to the current through it remains constant and equal to the resistance of the conductor.
$$\mathrm{R=\frac{V}{I}\:or\:V}=IR$$
$$\mathrm{∴V\:∝\:I}$$
Therefore, I-V characteristic is a straight line passing through the origin at all times.
Linear Resistor
A linear resistor is defined as a two terminal circuit element which satisfies Ohm’s law i.e. the voltage across the resistor is proportional to the current flowing through it. The linear resistor is also known as Ohmic resistor. It is represented by the symbol shown in figure.
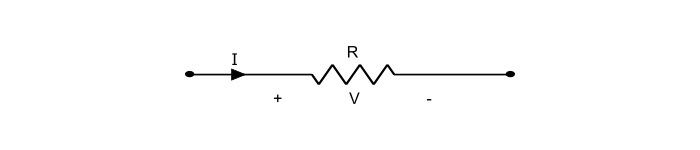
Ohm’s law states that, at all times
V=IR
Where, R is a constant called resistance of the linear resistor.
Characteristic Curve of Linear Resistor
The graph plotted between the Voltage across and current through the linear resistor is termed as characteristic curve of the linear resistor.
A two terminal element will be called a linear resistor if its voltage V and current I satisfy the following relation −
$$\mathrm{R={(V,I):f(V,I)=0}}$$
This relation is called I-V characteristic of the linear resistor and can be plotted in the I-V plane as shown below.
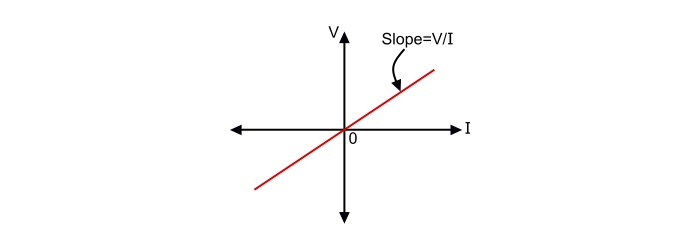
The characteristic of a linear resistor is always symmetric about the origin. The linear resistor is a special case of resistor in which
$$\mathrm{f(V,I)=V-IR=0}$$
There are two special cases of linear resistors viz. open circuit and short circuit.
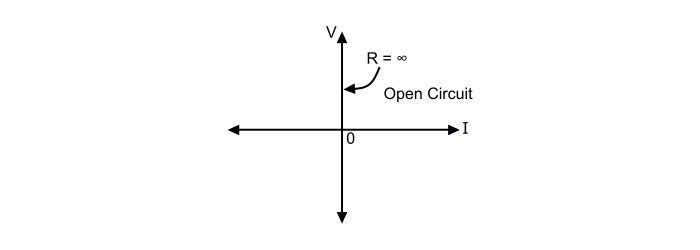
Open Circuit
A two terminal resistor is known as an open circuit if its current (I) is identically zero irrespective of the voltage (V), i.e., f(V,I) = I = 0. The characteristic of an open circuit is the V-axis in the I-V plane. It has an infinite slope, i.e., R = ∞.
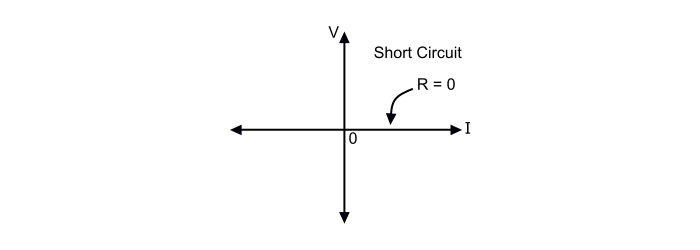
Short Circuit
A two terminal resistor is known as a short circuit if its voltage (V) is identically zero irrespective of its current (I), i.e., f(V,I) = V = 0. The characteristic of a short circuit is the I-axis in the I-V plane. The characteristic has a zero slope, i.e., R = 0.
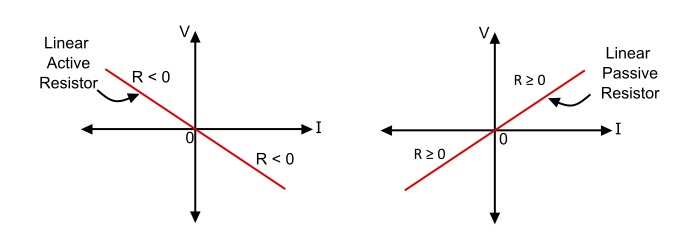
Note − The power delivered (p=I2R) to a linear resistor is always non-negative if R ≥ 0. A linear resistor is passive if its resistance is non-negative. Hence, a passive resistor always absorbs energy from the remainder of the circuit.
Also, the power delivered to a linear resistor is negative if R < 0 i.e. as current flows through it, the resistor delivers energy to the remainder of the circuit. Such a linear resistor with negative resistance is called an active resistor. The characteristic of a linear active resistor has negative slope.
Non-Linear Resistor
A resistor that is not linear is said to be non-linear resistor. Thus, a non-linear resistor can be defined as a resistance that does not obey the Ohm’s law. The non-linear resistor is an un-Ohmic device, i.e., its I-V characteristic is not a straight line.
Properties of Non-Linear Resistors
A non-linear resistor in general has a V-I characteristic which is not symmetric about origin of the V-I plane.
Non-linear resistor can produce harmonics in a circuit.
In general, the non-linear resistors hold neither homogeneity property nor additive property.
Characteristic Curve of Non-Linear Resistor
The graph plotted between the voltage across and the current through the non-linear resistor is known as the characteristic curve of the non-linear resistor.
There are a number of devices that represent the concept of non-linear resistance. Some of such devices are Ideal diode, pn-junction diode, Tunnel diode, Glow tube etc.
The characteristic of pn-junction diode can be used to explain the characteristic of a non-linear resistor.
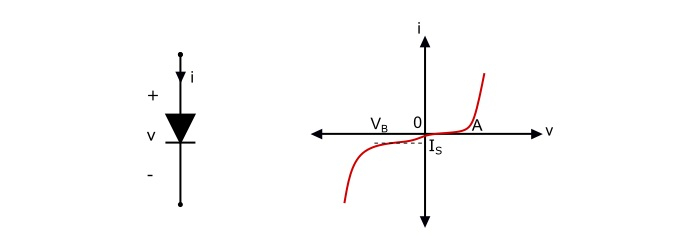
The pn-junction diode and its V-I characteristic is shown in the above figure. For most applications the device is operated to right of point VB, where VB is near to the knee point (A) of the curve. In the normal operating range, the current obeys the diode junction law.
$$\mathrm{i=I_{s}[exp(\frac{
u}{V_{T}})-1]}$$
Where,
IS is the reverse saturation current
VT = kT/e = Thermal voltage = about 0.026 V at room temperature k
k = Boltzmann’s constant
e = 1.6 X 10-19 C = charge on an electron
T = Temperature in Kelvins
Therefore, the above equation represents a non-linear resistor whose current (i) is expressed as a function of its voltage (v). Any non-linear resistor having this property is known as voltage controlled non-linear resistor.
Important Points
A pn-junction diode acts as a voltage controlled non-linear resistor.
Tunnel diode also behaves as a voltage controlled non-linear resistor.
A glow tube acts as a current controlled non-linear resistor.
An ideal diode is neither voltage controlled nor current controlled.
3K+ Views
