Absolute value of a number

---

---

Definition

The marks || (parallel bars) around a number give the absolute value of the number.

The absolute value of a number is its distance from 0 on the number line.

Also, the absolute value of any number (other than 0) is always positive.

Formula

|a|, the absolute value of a, is its distance a units from 0 on the number line.

For example

|9|, the absolute value of 9, is its distance 9 units from 0 on the number line

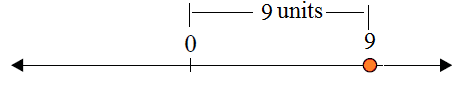
Similarly,

|12|, the absolute value of 12, is its distance 12 units from 0 on the number line

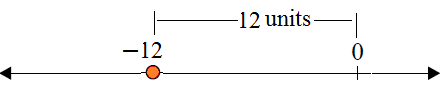
Example 1

Find the absolute value of the following number:

35

Solution

Step 1:

The absolute value of any number (other than 0) is always positive.

Step 2:

The absolute value of the number 35 is

|35| = 35

Example 2

Find the absolute value of the following number:

72

Solution

Step 1:

The absolute value of any number (other than 0) is always positive.

Step 2:

The absolute value of the number 72 is |72| = 72

Example 3

Find the following absolute value:

|92|

Solution

Step 1:

The absolute value of any number (other than 0) is always positive.

Step 2:

The absolute value is found by simplifying.

|92| = |7| = 7