Pitch Factor or Coil Span Factor in Alternator

Coil span or coil pitch is defined as the distance between the two sides of a coil.

Pole pitch is defined as the angular distance between the central line of one pole to the central line of the next pole. A pole pitch is always 180° electrical regardless of the number of poles on the machine.

• When a coil is having a span of 180° electrical, it is called as a full-pitch coil.

• When the coil is having a span less than 180° electrical, it is known as a short-pitch coil or fractional-pitch coil.

The fractional-pitch coil is also known as chorded coil. A stator winding using fractional pitch coil is called as a chorded winding.

If the span of the coil is reduced by an angle of electrical, then the coil span will be (180 − α) electrical degrees.

In case of a full-pitch coil, the two coil sides span a distance exactly equal to the pole pitch of 180° electrical. Consequently, the voltage generated in a full pitch coil is such that the coil-side voltages are in phase.

Let $𝐸_{𝐶1}$ and $𝐸_{𝐶2}$ are the voltages generated in the coil sides and $𝐸_{𝐶}$ is the resultant coil voltage. Then,

$$\mathrm{𝑬_{𝑪} = 𝑬_{𝑪𝟏} + 𝑬_{𝑪𝟐}}$$

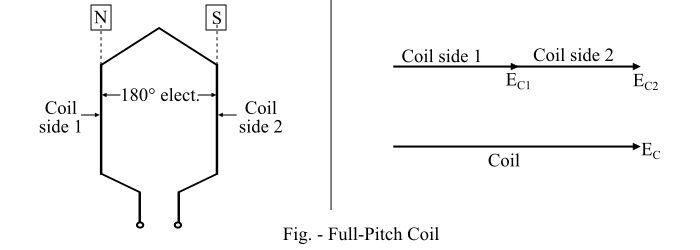
Since $𝐸_{𝐶1}$ and $𝐸_{𝐶2}$ are in phase, the resultant coil voltage is equal to their arithmetic sum (Refer the figure of full-pitch coil).

$$\mathrm{∴\:𝐸_{𝐶} = 𝐸_{𝐶1} + 𝐸_{𝐶2}}$$

If the coil span of a single coil is less than the pole pitch of 180° electrical, i.e., the case of short-pitch coil, the voltages generated in each coil side are not in phase. The resultant coil voltage $𝐸_{𝐶}$ is equal to the phasor sum of $𝐸_{𝐶1}$ and $𝐸_{𝐶2}$.

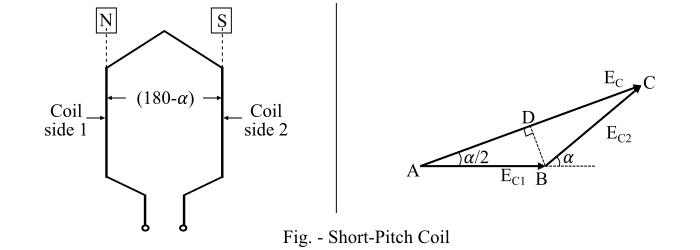
If the coil span is decreased by an angle of electrical, the coil span is (180 − α) electrical degree. The voltages generated $𝐸_{𝐶1}$ and $𝐸_{𝐶2}$ in the two coil sides will be out of phase with respect to each other by an angle of 𝛼° electrical. The phasor sum of $𝐸_{𝐶1}$ and $𝐸_{𝐶2}$ is $𝐸_{𝐶}$ = 𝐴𝐶(Refer the figure of short pitch coil).

The coil span-factor or pitch factor is defined as the ratio of the voltage generated in the short-pitch coil to the voltage generated in the full-pitch coil. The coil span factor is also known as chording factor.

$$\mathrm{Coil\:Span\:Factor, 𝑘_{𝐶} =\frac{Voltage \:generated\:with\:short − pitch\:coil}{Voltage \:generated\:with\:full\:pitch\:coil}}$$

Refer the phasor diagram,

$$\mathrm{𝑘_{𝐶} =\frac{Phasor\:sum\:of\:voltages \:of\:two\:coil\:sides}{Arithmetic\:sum\:of\:voltages \:of\:two\:coil\:sides}=\frac{𝐴𝐶}{2𝐴𝐵}}$$

$$\mathrm{\Rightarrow\:𝑘_{𝐶} =\frac{2𝐴𝐷}{2𝐴𝐵}= cos\left(\frac{α}{2}\right)}$$

For a full pitch coil,

$$\mathrm{α = 0°;\:\:\:cos\frac{α}{2}= 1;\:\:\:or\:\:\: 𝑘_{𝐶} = 1}$$

For a short pitch coil,

$$\mathrm{𝑘_{𝐶} < 1}$$

Advantages of Chording

The advantages of the chorded winding are as follows −

• There is a saving in the conductor material because the chording shortens the ends of the winding.

• The chording or short-pitching reduces the effects of distorting harmonics and hence the waveform of the generated voltage is improved and making it approach a sine wave.