Maxima & Minima Using First Derivative Test

Introduction

Usually, various physical entities are expressed in a mathematical equation that includes several variables. A function can represent the nature of variables during the process. A function can be graphically presented between the variable and the desired response. However, most of the time, we need to find the specific points at which the function gives a maximum and a minimum value. In this direction, the derivative test, which is a fundamental concept of calculus, is found to be quite helpful. In this tutorial, we will learn about the derivative, its application in optimization, and the determination of maxima and minima of a function using the first and second derivatives with solved examples.

Derivative

• The derivative is a fundamental concept in calculus.

• It is defined as the rate of change of one variable with another.

• In addition, it also refers to the slope of the tangent to the curve.

• The process of determining the derivative of a function is known as differentiation.

• The inverse process of the derivative is called integration or anti-differentiation.

• The differentiation of any arbitrary function (f(x)) is denoted as $\mathrm{\mathit{f}^Ι (x)\: or\: \frac{d\mathit{f}}{dx}}$.

• There are various formulae to determine the derivative of the various algebraic, trigonometric, logarithmic, and exponential functions.

Application of Derivatives in Optimization

The derivative concept has various applications in mathematics, physics, engineering, and finance. Among these, optimizing a process is an important discipline in industrial engineering, where derivatives play a vital role. Let’s discuss some real-life examples.

• The manufacturing industry sells a particular unit of products in a financial year. To maximize the profit, one must find the optimum unit of products to be sold. In this direction, the derivative helps in determining the maxima of the function.

• A minimum pressure drop is always desirable to obtain a lower energy cost during fluid pumping.

• The amount of material needs to be optimized to get a desirable container size.

Finding Maxima and Minima of a Function

In mathematics, the maxima and minima (plural of maximum and minimum) of a function represent the highest (maximum) and lowest (minimum) values of a function in the given range. These two extreme points can be determined using first and second derivative tests.

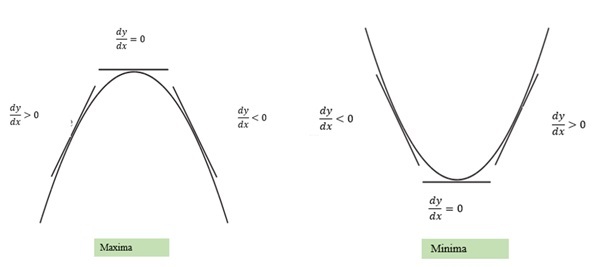
First Derivative Test

It is a simple method that involves the critical point in determining local maxima and minima. Let’s consider an arbitrary function $\mathrm{\mathit{f}(x)}$ and c is a critical point at which the function is continuous. Now, we have to follow the given steps to find the maxima and minima of a function.

• Evaluate the first derivative of the given function $\mathrm{\mathrm{(\mathit{f}(x)}), i.e., \mathit{f}^Ι (x) }$.

• In the second step, equalize the derivative of the function to zero, i.e., $\mathrm{\mathit{f}^Ι (x)=0 }$ and solve the equation to get limiting points.

• Find the neighbouring points of the obtained limiting points.

• Put those neighbouring points in the first derivative function, i.e., $\mathrm{\mathit{f}^Ι (x)}$.

• The limiting points are said to be maxima if $\mathrm{\mathit{f}^Ι (x)>0}$ towards its left and $\mathrm{\mathit{f}^Ι (x) < 0}$ towards its right.

• The limiting points are said to be minima if $\mathrm{\mathit{f}^Ι (x) < 0}$ towards its left and $\mathrm{\mathit{f}^Ι (x)>0}$ towards its right.

Second Derivative Test

The second derivative test is a systematic method to find the maxima and minima of a function. Let’s discuss the procedure to evaluate the local maxima and minima of a function using the second derivative test.

• Evaluate the first derivative of the given function $\mathrm{\mathrm{(\mathit{f}(x)}), i.e., \mathit{f}^Ι (x) }$.

• In the second step, equalize the derivative of the function to zero, i.e., $\mathrm{\mathit{f}^{Ι} (x) = 0}$ and solve the equation to get limiting points such as x₁,x₂, etc.

• Now, determine the second derivative of the original function $\mathrm{\mathit{f}^{ΙΙ} (x)}$.

• Now put those limiting points in $\mathrm{\mathit{f}^{ΙΙ} (x)}$.

• The limiting point x_1is said to be local maxima if $\mathrm{\mathit{f}^{ΙΙ} (x) < 0}$.

• The limiting point x_1is said to be local minima if $\mathrm{\mathit{f}^{ΙΙ} (x) > 0}$.

Solved Examples

Example 1:

Let’s consider a function f(x)=x³-3x+2. Find the maxima and minima of the function using the first derivative test.

Solution:

We will use the following steps to find the maxima and minima of the function.

• Step 1: It is given that, f(x)=x³-3x+2.

  Then f^Ι(x)=3x²-3.

• Take f^Ι(x)=0

  $\mathrm{\Rightarrow 3x^2-3=0}$

  $\mathrm{\Rightarrow 3(x^2-1)=0}$

  $\mathrm{\Rightarrow 3(x+1)(x-1)=0}$

  ⇒x=-1,1 (Limiting points)

• The neighbouring points of (-1,1) is (-2, 0) and (0, 2).

• $\mathrm{\mathit{f}^Ι (-2)=3(-2)^2-3=9,\mathit{f}^Ι (0)=3(0)^2-3=-3}$

• The limiting point (-2, 0) is said to be local maxima since if $\mathrm{\mathit{f}^{Ι} (x) < 0}$ towards its left and $\mathrm{\mathit{f}^{Ι} (x) > 0}$ towards its right.

• $\mathrm{\mathit{f}^Ι (0)=3(0)^2-3=-3,\mathit{f}^Ι (2)=3(2)^2-3=9}$

• The limiting point (0, 2) is said to be minima since $\mathrm{\mathit{f}^{Ι} (x) < 0}$ towards its left and $\mathrm{\mathit{f}^{Ι} (x) > 0}$ towards its right.

∴ The local maxima and minima of the function are (-1) and (1), respectively.

Example 2:

Let’s consider a function f(x)=5x³+4x²+x+7. Find the maxima and minima of the function using the second derivative test.

Solution:

We will use the following steps to find the maxima and minima of the function.

• Step 1 − It is given that, f(x)=5x³+4x²+x+7.

  $\mathrm{Then \: \mathit{f}^Ι (x)=15x^2+8x+1.}$

• $$\mathrm{Take\: \mathit{f}^Ι(x)=15x^2+8x+1=0 }$

$\mathrm{\Rightarrow 15x^2+5x+3x+1=0}$

$\mathrm{\Rightarrow 5x(3x+1)+1(3x+1)=0}$

$\mathrm{\Rightarrow (3x+1)(5x+1)=0}$

$\mathrm{\Rightarrow x=\frac{-1}{3},\frac{-1}{5} (Limiting\: points)}$$

• $$\mathrm{\mathit{f}^{ΙΙ} (x)=30x+8.}$

• Now we will substitute the limiting point in $\mathrm{\mathit{f}^{ΙΙ}(x)}$.

• $\mathrm{\mathit{f}^{ΙΙ}(\frac{-1}{3})=30(\frac{-1}{3})+8=-2 < 0}$

  The limiting point $\mathrm{\frac{-1}{3}}$is said to be local maxima since $\mathrm{\mathit{f}^{ΙΙ}(\frac{-1}{3})< 0}$

• $\mathrm{\mathit{f}^{ΙΙ}(\frac{-1}{5})=30(\frac{-1}{5})+8=2 < 0}$

  The limiting point $\mathrm{\frac{-1}{5}}$is said to be local minima since $\mathrm{\mathit{f}^{ΙΙ}(\frac{-1}{5})> 0}$

∴ The local maxima and minima of the function are $\mathrm{(\frac{-1}{3})}$ and $\mathrm{(\frac{-1}{5})}$, respectively.

Conclusion

The present tutorial gives a brief introduction to the maxima and minima of a function. The basic definition of local extreme points (maxima and minima) and derivatives have been stated in this tutorial. In addition, the procedure to determine the maxima and minima using the first derivative and second derivative tests have been illustrated. Moreover, some solved examples have been provided for better clarity of this concept. In conclusion, the present tutorial may be useful for understanding concept of maxima and minima and their evaluation using the first and second derivative tests .

FAQs

1.Give an example of a function that has no minima and maxima?

The set of real numbers has no maxima and minima.

2.Which method is more effective in determining the minima and maxima of a function?

The first-derivative test is an effective method to find the minima and maxima of the function. Because the second derivative test fails if there is no second derivative of the function exists. In that case, we only have to evaluate the extreme points using the first derivative test.

3.Why does the first derivative test fail?

The first derivative test fails if the obtained limiting points are not the local maxima or minima.

4.What are the applications of derivatives?

The derivative concept helps to find the concavity of the graph, inflection point, local maxima, and minima.

5.How do you define a critical point?

A point (c) is said to be a critical point for the function $\mathrm{\mathit{f}(x)\mathit{f}^Ι(c)=0\: or \: \mathit{f}^Ι(x)}$ does not exist.