Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Linear Regression using Python?
Linear regression is one of the simplest standard tool in machine learning to indicate if there is a positive or negative relationship between two variables.
Linear regression is one of the few good tools for quick predictive analysis. In this section we are going to use python pandas package to load data and then estimate, interpret and visualize linear regression models.
Before we go down further down, let’s discuss what is regression first?
What is Regression?
Regression is a form of predictive modelling technique which helps in creating a relationship between a dependent and independent variable.
Types of Regression
- Linear Regression
- Logistic Regression
- Polynomial Regression
- Stepwise Regression
Where is Linear Regression Used?
- Evaluating Trends and Sales Estimates
- Analysing the Impact of Price Changes
- Assessing Risk
Steps to build our linear regression model
Firstly we are going to build the setup and downloading the dataset and the jupyter(which i’m using for this tutorial, you can use other IDE like anaconda or like).
Import the required package and dataset.
With our dataset loaded, we’re going to explore our dataset.
Will do linear regression with our dataset
Then we’ll explore the relationship between our variable and Time of day.
Summary.
Setup
You can download the dataset from below link,
http://en.openei.org/datasets/dataset/649aa6d3-2832-4978-bc6e-fa563568398e/resource/b710e97d-29c9-4ca5-8137-63b7cf447317/download/building1retail.csv
which we are going to use to model the power of a building using the Outdoor Air Temperature (OAT) as an explanatory variable.
Save the csv file in the same folder where our jupyter or IDE is installed.
Import Required libraries and dataset
Firstly we are going to import the required libraries and then read the dataset using pandas python library.
# Importing Necessary Libraries
import pandas as pd
#Required for numerical functions
import numpy as np
from scipy import stats
from datetime import datetime
from sklearn import preprocessing
from sklearn.model_selection import KFold
from sklearn.linear_model import LinearRegression
#For plotting the graph
import matplotlib.pyplot as plt
%matplotlib inline
# Reading Data
df = pd.read_csv('building1retail.csv', index_col=[0],
date_parser=lambda x: datetime.strptime(x, "%m/%d/%Y %H:%M"))
df.head()Output
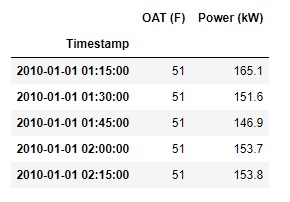
Exploring the Dataset
So let’s first visualize our dataset by plotting it with pandas.
df.plot(figsize=(22,6))
Output
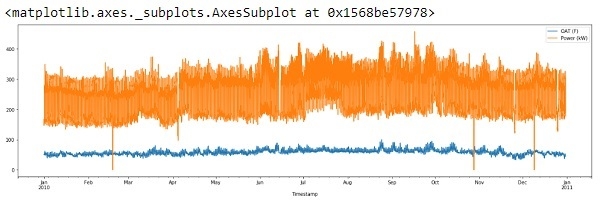
So, the x-axis is showing data from Jan2010 – Jan2011.
If we see above output, we can notice there are two odd things about the plot:
There seems to be no missing data, To check it out, just run:
df.isnull().values.any()
Output
False
False result is telling us there is no null values in the dataframe.
It appears, there is some anomalies in the data (long downward spikes)
The anomalies or ‘outliers’ are generally the result of an experimental error or may be the true value. In either case, we are going to discard it as they severely affect the slope of regression line.
Before we discard the ‘outliers’, lets first check what kind of distribution our data is representing:
df.hist()
Output
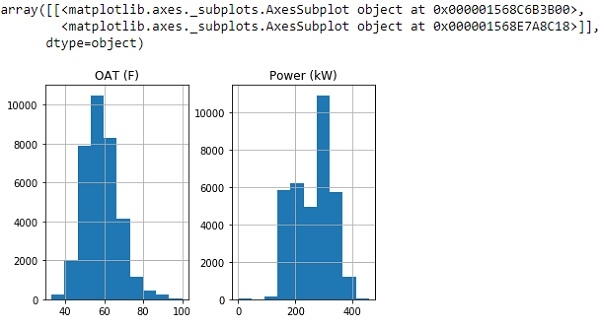
From above histogram, we can see our graph is showing the data that roughly follows a normal distribution.
So let’s drop all values that are greater than 3 standard deviations from the mean and plot the new dataframe.
std_dev = 3 df = df[(np.abs(stats.zscore(df)) < float(std_dev)).all(axis=1)] df.plot(figsize=(22, 6))
Output
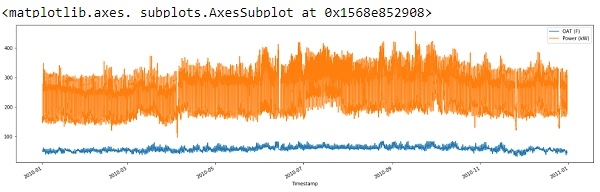
So from above output we can see, we have removed the spikes to some extent and cleaned our data.
Validate linear relationship
To find if there is any linear relation between the OAT and Power, let’s plot a simple scatter plot:
plt.scatter(df['OAT (F)'], df['Power (kW)'])
Output
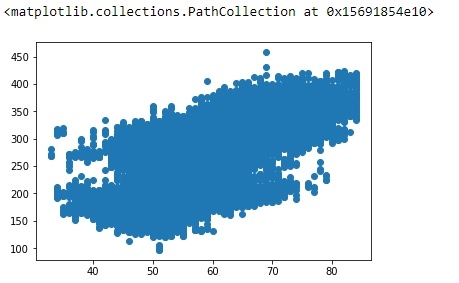
Linear Regression
To run models and assess it performance we are going to use the Scikit-learn module also, we are going to use the k-folds cross validation (k=3) to assess the performance of our model.
X = pd.DataFrame(df['OAT (F)']) y = pd.DataFrame(df['Power (kW)']) model = LinearRegression() scores = [] kfold = KFold(n_splits=3, shuffle=True, random_state=42) for i, (train, test) in enumerate(kfold.split(X, y)): model.fit(X.iloc[train,:], y.iloc[train,:]) score = model.score(X.iloc[test,:], y.iloc[test,:]) scores.append(score) print(scores)
Output
[0.38768927735902703, 0.3852220878090444, 0.38451654781487116]
In above program, the model = LinearRegression() creates a linear regression model and the for loop divides the dataset into three folds. Then inside the loop, we fit the data and then assess its performance by appending its score to a list.
However, the results doesn’t look good and we can improve it’s performance.
Time of Day
The power (variable) is highly dependent on the time of day. Let’s use this information to incorporate it into our regression model by using one-hot encoding.
model = LinearRegression() scores = [] kfold = KFold(n_splits=3, shuffle=True, random_state=42) for i, (train, test) in enumerate(kfold.split(X, y)): model.fit(X.iloc[train,:], y.iloc[train,:]) scores.append(model.score(X.iloc[test,:], y.iloc[test,:])) print(scores)
Output
[0.8074246958895391, 0.8139449185141592, 0.8111379602960773]
That’s a big difference we have in our model.
Summary
In this section, we learned the basics of exploring a dataset and preparing it to fit to a regression model. We assessed its performance, detected its shortcomings and fixed it.
512 Views
