Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Linear Regression using PyTorch?
About Linear Regression
Simple Linear Regression Basics
Allows us to understand relationship between two continuous variable.
Example −
x = independent variable
weight
y = dependent variable
height
y = αx + β
Let's understand simple linear regression through a program −
#Simple linear regression import numpy as np import matplotlib.pyplot as plt np.random.seed(1) n = 70 x = np.random.randn(n) y = x * np.random.randn(n) colors = np.random.rand(n) plt.plot(np.unique(x), np.poly1d(np.polyfit(x, y, 1))(np.unique(x))) plt.scatter(x, y, c = colors, alpha = 0.5) plt.show()
Output
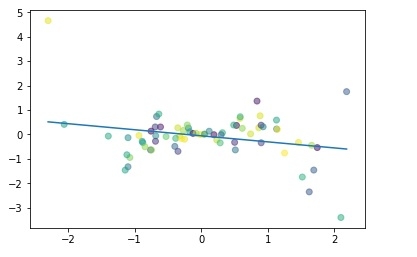
Purpose of Linear Regression:
to Minimize the distance between the points and the line (y = αx + β)
Adjusting
Coefficient: α
Intercept/Bias: β
Building a Linear Regression Model with PyTorch
Let's suppose our coefficient (α) is 2 and intercept (β) is 1 then our equation will become −
y = 2x +1 #Linear model
Building the Dataset
x_values = [i for i in range(11)] x_values
Output
[0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
#convert to numpy
x_train = np.array(x_values, dtype = np.float32) x_train.shape
Output
(11,)
#Important: 2D required x_train = x_train.reshape(-1, 1) x_train.shape
Output
(11, 1)
y_values = [2*i + 1 for i in x_values] y_values
Output
[1, 3, 5, 7, 9, 11, 13, 15, 17, 19, 21]
#list iteration y_values = [] for i in x_values: result = 2*i +1 y_values.append(result) y_values
Output
[1, 3, 5, 7, 9, 11, 13, 15, 17, 19, 21]
y_train = np.array(y_values, dtype = np.float32) y_train.shape
Output
(11,)
#2D required y_train = y_train.reshape(-1, 1) y_train.shape
Output
(11, 1)
Building Model
#import libraries
import torch
import torch.nn as nn
from torch.autograd import Variable
#Create Model class
class LinearRegModel(nn.Module):
def __init__(self, input_size, output_size):
super(LinearRegModel, self).__init__()
self.linear = nn.Linear(input_dim, output_dim)
def forward(self, x):
out = self.linear(x)
return out
input_dim = 1
output_dim = 1
model = LinearRegModel(input_dim, output_dim)
criterion = nn.MSELoss()
learning_rate = 0.01
optimizer = torch.optim.SGD(model.parameters(), lr = learning_rate)
epochs = 100
for epoch in range(epochs):
epoch += 1
#convert numpy array to torch variable
inputs = Variable(torch.from_numpy(x_train))
labels = Variable(torch.from_numpy(y_train))
#Clear gradients w.r.t parameters
optimizer.zero_grad()
#Forward to get output
outputs = model.forward(inputs)
#Calculate Loss
loss = criterion(outputs, labels)
#Getting gradients w.r.t parameters
loss.backward()
#Updating parameters
optimizer.step()
print('epoch {}, loss {}'.format(epoch, loss.data[0]))Output
epoch 1, loss 276.7417907714844 epoch 2, loss 22.601360321044922 epoch 3, loss 1.8716105222702026 epoch 4, loss 0.18043726682662964 epoch 5, loss 0.04218350350856781 epoch 6, loss 0.03060017339885235 epoch 7, loss 0.02935197949409485 epoch 8, loss 0.02895027957856655 epoch 9, loss 0.028620922937989235 epoch 10, loss 0.02830091118812561 ...... ...... epoch 94, loss 0.011018744669854641 epoch 95, loss 0.010895680636167526 epoch 96, loss 0.010774039663374424 epoch 97, loss 0.010653747245669365 epoch 98, loss 0.010534750297665596 epoch 99, loss 0.010417098179459572 epoch 100, loss 0.010300817899405956
So we can the loss is reduced considerably from epoch 1 to epoch 100.
Plot the graph
#Purely inference predicted = model(Variable(torch.from_numpy(x_train))).data.numpy() predicted y_train #Plot Graph #Clear figure plt.clf() #Get predictions predicted = model(Variable(torch.from_numpy(x_train))).data.numpy() #Plot true data plt.plot(x_train, y_train, 'go', label ='True data', alpha = 0.5) #Plot predictions plt.plot(x_train, predicted, '--', label='Predictions', alpha = 0.5) #Legend and Plot plt.legend(loc = 'best') plt.show()
Output
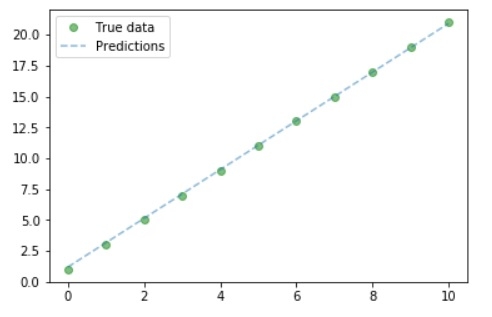
So we can from the graph- our true and predicted value almost similar.
Updated on: 30-Jul-2019
412 Views
Advertisements