Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Linear Regression
From a given set of data points, the linear regression finds an equation of straight line. The given points will follow the straight line. Using this formula, we can predict what will be the value for some other specific point, which is not present in the set currently.
For solving linear regression problems using some data points, we have to follow these formulae:
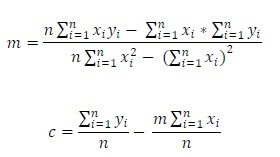
Here the m and c are the slope and the y-intercept respectively. Using these expressions, we can get the equation of straight line in this form: 𝑦 = 𝑚𝑥 + 𝑐.
Input and Output
Input:
The (x, y) coordinates of some points. {(1,3), (2,4), (3,5), (4,6), (5,8)}
Output:
The slope: 1.2 The Intercept: 1.6
The equation: y = 1.2x + 1.6Algorithm
linReg(coord)
Input: The given set of coordinate points.
Output: The slope m and y-intercept c.
Begin for i := 1 to n, do sumX := sumX + coord[i,0] sumY := sumY + coord[i,1] sumXsq := sumXsq + (coord[i,0]*coord[i,0]) sumXY := sumXY + (coord[i,0] * coord[i,1]) done m := (n * sumXY – (sumX*sumY)) / (n * sumXsq – (sumX * sumX)) c := (sumY / n) – (m * sumX)/n End
Example
#include<iostream>
#include<cmath>
#define N 5
using namespace std;
void linReg(int coord[N][2], float &m, float &c) {
float sx2 = 0, sx = 0, sxy = 0, sy = 0;
for(int i = 0; i<N; i++) {
sx += coord[i][0]; //sum of x
sy += coord[i][1]; //sum of y
sx2 += coord[i][0]*coord[i][0]; //sum of x^2
sxy += coord[i][0]*coord[i][1]; //sum of x*y
}
// finding slope and intercept
m = (N*sxy-(sx*sy))/(N*sx2-(sx*sx));
c = (sy/N)-(m*sx)/N;
}
main() {
// this 2d array holds coordinate points
int point[N][2] = {{1,3},{2,4},{3,5},{4,6},{5,8}};
float m, c;
linReg(point, m, c);
cout << "The slope: " << m << " The Intercept: " << c << endl;
cout << "The equation: " << "y = "<< m <<"x + "<< c;
}Output
The slope: 1.2 The Intercept: 1.6 The equation: y = 1.2x + 1.6
Updated on: 17-Jun-2020
719 Views
Advertisements