Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Isomorphism
A graph can exist in different forms having the same number of vertices, edges, and also the same edge connectivity. Such graphs are called isomorphic graphs. Note that we label the graphs in this chapter mainly for the purpose of referring to them and recognizing them from one another.
Isomorphic Graphs
Two graphs G1 and G2 are said to be isomorphic if −
- Their number of components (vertices and edges) are same.
- Their edge connectivity is retained.
Note − In short, out of the two isomorphic graphs, one is a tweaked version of the other. An unlabelled graph also can be thought of as an isomorphic graph.
There exists a function 'f' from vertices of G1 to vertices of G2
[f: V(G1) ⇒ V(G2)], such that
Case (i): f is a bijection (both one-one and onto)
Case (ii): f preserves adjacency of vertices, i.e., if the edge {U, V} ∈ G1, then the
edge {f(U), f(V)} ∈ G2, then G1 = G2.Note
If G1 = G2 then −
|V(G1)| = |V(G2)|
|E(G1)| = |E(G2)|
Degree sequences of G1 and G2 are same.
If the vertices {V1, V2, .. Vk} form a cycle of length K in G1, then the vertices {f(V1), f(V2),… f(Vk)} should form a cycle of length K in G2.
All the above conditions are necessary for the graphs G1 and G2 to be isomorphic, but not sufficient to prove that the graphs are isomorphic.
(G1 = G2) if and only if (G1− = G2−) where G1 and G2 are simple graphs.
(G1 = G2) if the adjacency matrices of G1 and G2 are same.
(G1 = G2) if and only if the corresponding subgraphs of G1 and G2 (obtained by deleting some vertices in G1 and their images in graph G2) are isomorphic.
Example
Which of the following graphs are isomorphic?
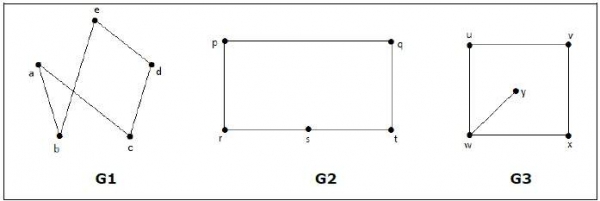
In the graph G3, vertex 'w' has only degree 3, whereas all the other graph vertices has degree 2. Hence G3 not isomorphic to G1 or G2.
Taking complements of G1 and G2, you have −
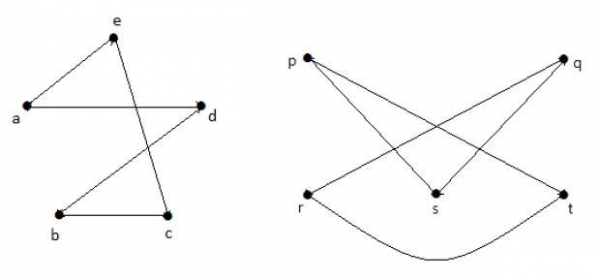
Here, (G1− = G2−), hence (G1 = G2).
555 Views
