
 Data Structure
Data Structure Networking
Networking RDBMS
RDBMS Operating System
Operating System Java
Java MS Excel
MS Excel iOS
iOS HTML
HTML CSS
CSS Android
Android Python
Python C Programming
C Programming C++
C++ C#
C# MongoDB
MongoDB MySQL
MySQL Javascript
Javascript PHP
PHP
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Basic Concepts of Graphs
A graph is a set of points, called nodes or vertices, which are interconnected by a set of lines called edges. The study of graphs, or graph theory is an important part of a number of disciplines in the fields of mathematics, engineering and computer science.
Graph Theory
Definition − A graph (denoted as G = (V, E)) consists of a non-empty set of vertices or nodes V and a set of edges E. A vertex a represents an endpoint of an edge. An edge joins two vertices a, b and is represented by set of vertices it connects.
Example − Let us consider, a Graph is G = (V, E) where V = {a, b, c, d} and E = {{a, b}, {a, c}, {b, c}, {c, d}}
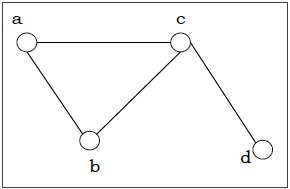
Degree of a Vertex − The degree of a vertex V of a graph G (denoted by deg (V)) is the number of edges incident with the vertex V.
| Vertex | Degree | Even / Odd |
|---|---|---|
| a | 2 | even |
| b | 2 | even |
| c | 3 | odd |
| d | 1 | odd |
Even and Odd Vertex − If the degree of a vertex is even, the vertex is called an even vertex and if the degree of a vertex is odd, the vertex is called an odd vertex.
Degree of a Graph − The degree of a graph is the largest vertex degree of that graph. For the above graph the degree of the graph is 3.
The Handshaking Lemma − In a graph, the sum of all the degrees of all the vertices is equal to twice the number of edges. For example, in above case, sum of all the degrees of all vertices is 8 and total edges are 4.

