
- Automata Theory - Applications
- Automata Terminology
- Basics of String in Automata
- Set Theory for Automata
- Finite Sets and Infinite Sets
- Algebraic Operations on Sets
- Relations Sets in Automata Theory
- Graph and Tree in Automata Theory
- Transition Table in Automata
- What is Queue Automata?
- Compound Finite Automata
- Complementation Process in DFA
- Closure Properties in Automata
- Concatenation Process in DFA
- Language and Grammars
- Language and Grammar
- Grammars in Theory of Computation
- Language Generated by a Grammar
- Chomsky Classification of Grammars
- Context-Sensitive Languages
- Finite Automata
- What is Finite Automata?
- Finite Automata Types
- Applications of Finite Automata
- Limitations of Finite Automata
- Two-way Deterministic Finite Automata
- Deterministic Finite Automaton (DFA)
- Non-deterministic Finite Automaton (NFA)
- NDFA to DFA Conversion
- Equivalence of NFA and DFA
- Dead State in Finite Automata
- Minimization of DFA
- Automata Moore Machine
- Automata Mealy Machine
- Moore vs Mealy Machines
- Moore to Mealy Machine
- Mealy to Moore Machine
- Myhill–Nerode Theorem
- Mealy Machine for 1’s Complement
- Finite Automata Exercises
- Complement of DFA
- Regular Expressions
- Regular Expression in Automata
- Regular Expression Identities
- Applications of Regular Expression
- Regular Expressions vs Regular Grammar
- Kleene Closure in Automata
- Arden’s Theorem in Automata
- Convert Regular Expression to Finite Automata
- Conversion of Regular Expression to DFA
- Equivalence of Two Finite Automata
- Equivalence of Two Regular Expressions
- Convert Regular Expression to Regular Grammar
- Convert Regular Grammar to Finite Automata
- Pumping Lemma in Theory of Computation
- Pumping Lemma for Regular Grammar
- Pumping Lemma for Regular Expression
- Pumping Lemma for Regular Languages
- Applications of Pumping Lemma
- Closure Properties of Regular Set
- Closure Properties of Regular Language
- Decision Problems for Regular Languages
- Decision Problems for Automata and Grammars
- Conversion of Epsilon-NFA to DFA
- Regular Sets in Theory of Computation
- Context-Free Grammars
- Context-Free Grammars (CFG)
- Derivation Tree
- Parse Tree
- Ambiguity in Context-Free Grammar
- CFG vs Regular Grammar
- Applications of Context-Free Grammar
- Left Recursion and Left Factoring
- Closure Properties of Context Free Languages
- Simplifying Context Free Grammars
- Removal of Useless Symbols in CFG
- Removal Unit Production in CFG
- Removal of Null Productions in CFG
- Linear Grammar
- Chomsky Normal Form (CNF)
- Greibach Normal Form (GNF)
- Pumping Lemma for Context-Free Grammars
- Decision Problems of CFG
- Pushdown Automata
- Pushdown Automata (PDA)
- Pushdown Automata Acceptance
- Deterministic Pushdown Automata
- Non-deterministic Pushdown Automata
- Construction of PDA from CFG
- CFG Equivalent to PDA Conversion
- Pushdown Automata Graphical Notation
- Pushdown Automata and Parsing
- Two-stack Pushdown Automata
- Turing Machines
- Basics of Turing Machine (TM)
- Representation of Turing Machine
- Examples of Turing Machine
- Turing Machine Accepted Languages
- Variations of Turing Machine
- Multi-tape Turing Machine
- Multi-head Turing Machine
- Multitrack Turing Machine
- Non-Deterministic Turing Machine
- Semi-Infinite Tape Turing Machine
- K-dimensional Turing Machine
- Enumerator Turing Machine
- Universal Turing Machine
- Restricted Turing Machine
- Convert Regular Expression to Turing Machine
- Two-stack PDA and Turing Machine
- Turing Machine as Integer Function
- Post–Turing Machine
- Turing Machine for Addition
- Turing Machine for Copying Data
- Turing Machine as Comparator
- Turing Machine for Multiplication
- Turing Machine for Subtraction
- Modifications to Standard Turing Machine
- Linear-Bounded Automata (LBA)
- Church's Thesis for Turing Machine
- Recursively Enumerable Language
- Computability & Undecidability
- Turing Language Decidability
- Undecidable Languages
- Turing Machine and Grammar
- Kuroda Normal Form
- Converting Grammar to Kuroda Normal Form
- Decidability
- Undecidability
- Reducibility
- Halting Problem
- Turing Machine Halting Problem
- Rice's Theorem in Theory of Computation
- Post’s Correspondence Problem (PCP)
- Types of Functions
- Recursive Functions
- Injective Functions
- Surjective Function
- Bijective Function
- Partial Recursive Function
- Total Recursive Function
- Primitive Recursive Function
- μ Recursive Function
- Ackermann’s Function
- Russell’s Paradox
- Gödel Numbering
- Recursive Enumerations
- Kleene's Theorem
- Kleene's Recursion Theorem
- Advanced Concepts
- Matrix Grammars
- Probabilistic Finite Automata
- Cellular Automata
- Reduction of CFG
- Reduction Theorem
- Regular expression to ∈-NFA
- Quotient Operation
- Parikh’s Theorem
- Ladner’s Theorem
Deterministic Finite Automaton
DFA refers to deterministic finite automata. Deterministic refers to the uniqueness of the computation. The finite automata are deterministic FA, if the machine reads an input string one symbol at a time.
In DFA, there is only one path input from the current state to the next state. It does not accept the null move, i.e. it cannot change state without any input. It can contain multiple final states. It is used in Lexical Analysis in compilers.
Finite Automaton can be classified into two types −
- Deterministic Finite Automaton (DFA)
- Non-deterministic Finite Automaton (NDFA / NFA)
Deterministic Finite Automaton (DFA)
In DFA, for each input symbol, one can determine the state to which the machine will move. Hence, it is called Deterministic Automaton. As it has a finite number of states, the machine is called Deterministic Finite Machine or Deterministic Finite Automaton.
Formal Definition of a DFA
A Deterministic Finite automata (DFA) is a collection of defined as a 5-tuples and is as follows −
$$\mathrm{M \:=\:(Q,\: \Sigma,\: \delta, \:q0,\:F)}$$
Where,
- Q is a finite set of states.
- ∑ is a finite set of symbols called the alphabet.
- δ is the transition function where δ: Q × ∑ → Q
- q0 is the initial state from where any input is processed (q0 ∈ Q).
- F is a set of final state/states of Q (F ⊆ Q).
Graphical Representation of a DFA
A DFA is represented by digraphs called state diagram.
- The vertices represent the states.
- The arcs labeled with an input alphabet show the transitions.
- The initial state is denoted by an empty single incoming arc.
- The final state is indicated by double circles.
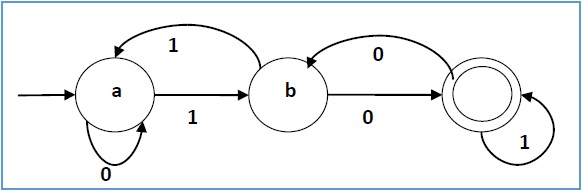
Example 1
Let a deterministic finite automaton be →
- Q = {a, b, c},
- ∑ = {0, 1},
- q0 = {a},
- F = {c}, and
Transition Table
Transition function δ as shown by the following table −
| Present State | Next State for Input 0 | Next State for Input 1 |
|---|---|---|
| a | a | b |
| b | c | a |
| c | b | c |
Its graphical representation would be as follows −
Example 2
Minimize the following DFA
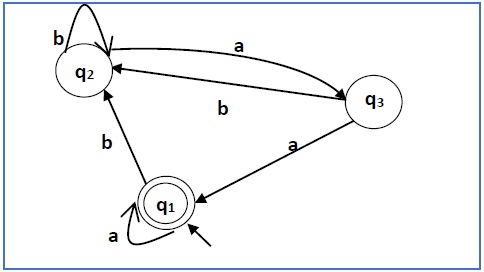
Solution
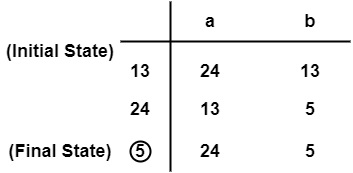
Make a transition Table.
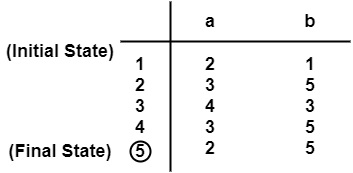
$$\mathrm{\pi_0 \:=\: \{\{5\},\: \{1,\: 2,\: 3,\: 4\}\}}$$
$$\mathrm{\text{For input a, on }\: \{1,\:,2,\:3,\:4\} \: of \: \pi_0 }$$

For input b, on {1, 2, 3, 4} of π0
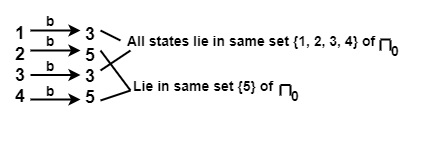
$$\mathrm{\therefore \: \{1,\: 2,\: 3,\: 4\}\: \text{ will be split into } \: \{1, 3\} \: and \: \{2, 4\}}$$
$$\mathrm{\therefore \: \pi_1 \:=\: \{\{5\}, \:\{1, \:3\},\:\{2,\:4\}\}}$$
For input symbol a on {1, 3} of π1
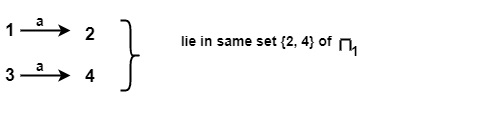
Similarly for input symbol a on {2, 4} of π1
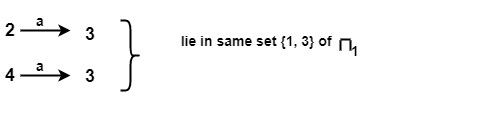
For input symbol b on {1, 3} of π1
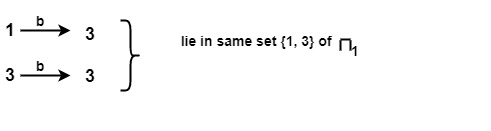
Similarly for input symbol b on {2, 4} of π1
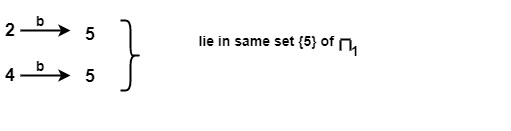
Subset in π1 i.e., {1, 3} & {2, 4} will not be splitted.
$$\mathrm{\pi_{final} \:=\: \{\{5\},\: \{1,\: 3\},\: \{2,\: 4\}\}}$$
There will be 3 states of DFA.
$$\mathrm{\{5\},\: \{1,\: 3\} \:and \:\{2,\: 4\}}$$
Minimized DFA will be −
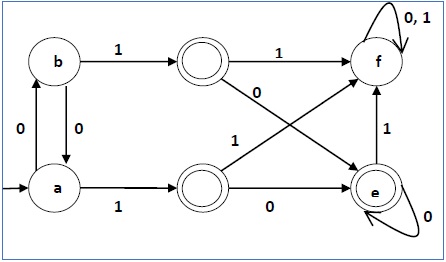
Example 3
Given a Deterministic Finite Automata (DFA), try to reduce the DFA by removing unreachable states and removing similar rows.
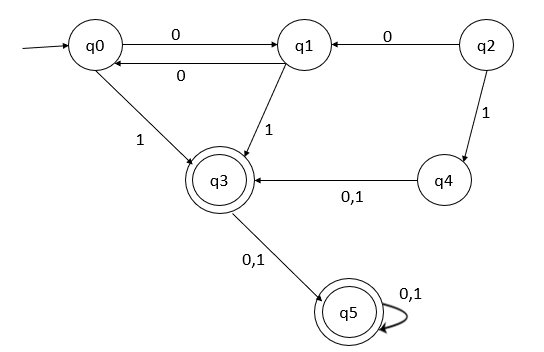
Solution
Step 1 − Remove the unreachable states from q0
From the initial states, we are not able to reach q2 and q4. So, remove these two states as shown below −

After removing unreachable states, the partial minimized DFA is as follows −
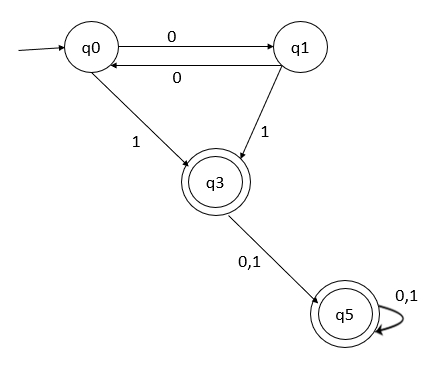
Step 2 − The transition table is given below −
| States | 0 | 1 |
|---|---|---|
| → q0 | q1 | q3 |
| q1 | q0 | q3 |
| *q3 | q5 | q5 |
| *q5 | q5 | q5 |
Step 3 − Divide tables into 2 tables as shown below −
Table 1 starts from the non-final states.
| States | 0 | 1 |
|---|---|---|
| → q0 | q1 | q3 |
| q1 | q0 | q3 |
Table 2 starts from the final states.
| States | 0 | 1 |
|---|---|---|
| *q3 | q5 | q5 |
| *q5 | q5 | q5 |
Step 4 − Remove similar rows.
Table 1 has no similar rows
Table 2 has similar rows. So, skip q5 and replace q5 by q3
| States | 0 | 1 |
|---|---|---|
| q3 | q5 | q3 |
Step 5 − Combine two tables as shown below −
| States | 0 | 1 |
|---|---|---|
| → q0 | q1 | q3 |
| q1 | q0 | q3 |
| *q3 | q3 | q3 |
Thus, the minimized DFA will be as follows −

Trap State in DFA
If a transition goes to a state from which it can never escape. Such a state is called a trap state. It is called the dead state.
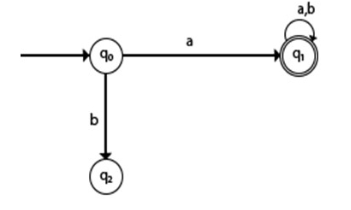
In the above example, q2 is a trap or dead state because it can't reach the final state.
Application of Deterministic Finite Automata (DFA)
The different applications of deterministic finite automata are as follows −
- Protocol analysis text parsing.
- Video game character behavior.
- Security analysis.
- CPU control units.
- Natural language processing Speech recognition, etc.