Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Construct the full k-ary tree from its preorder traversal in C++
We are given an array arr[] containing the preorder traversal of the k-ary tree in sequence. The goal is to construct the same k-ary tree from it and print its postorder traversal. A full k−ary tree is the one in which the root node has 0 or k children i.e. at most k child.
For Example
Input
int arr[] = {2, 5, 1, 3, 6, 7, 2, 1 }, int size = 8, int children = 2Output
The full k−ary tree which will be constructed with the two children from preorder traversal is given below −
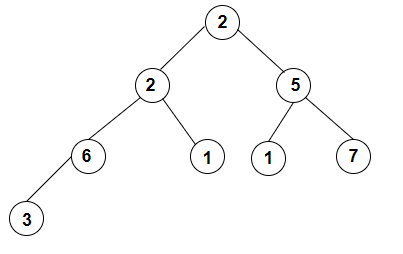
Explanation
we are given with an array of integer values or the preorder traversal of a tree with the k children which is 2. So, the tree formed will have postorder traversal as 3 6 1 2 1 7 5 2 which is constructed as per the rule that says visit all LEFT Subtree nodes then visit all RIGHT Subtree nodes and then visit all ROOT nodes.
Input
int arr[] = {2, 5, 1, 3, 6, 7, 2, 1 }, int size = 8, int children = 3Output
The full k−ary tree which will be constructed with the three children from preorder traversal is given below −
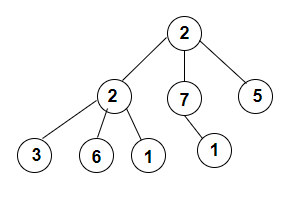
Explanation
we are given with an array of integer values or the preorder traversal of a tree with the k children which is 3. So, the tree formed will have postorder traversal as 3 6 1 2 1 7 5 2 which is constructed as per the rule that says visit all LEFT Subtree nodes then visit all RIGHT Subtree nodes and then visit all ROOT nodes.
Approach used in the below program is as follows −
In this approach we will first construct the k-ary tree from the given array taking the first element as the root node. If the left subtree is empty then the right one will also be empty. Recursively call for left and right subtrees and link them. For the postorder traversal we take left subtree, then right subtree and then print the weight of the node.
Call postorder(root−>left)
Call postorder(root−>right)
Print root−>data
Take arr[] as an input array containing the preorder traversal.
Take k as variable children.
Take the starting index as count=0.
Construct tree using Tree_Node* node = create_tree(arr, size, children, count).
Function new_Node(int data) generates a new node of tree.
Function create_tree(int arr[], int N, int k, int height, int& count) generates the kary tree from the array arr[].
If the number of nodes is <=0 then return NULL, no tree can be constructed.
Initialize newNode = new_Node(arr[count]), the first element of arr[].
If (newNode == NULL) results true then no tree possible.
Traverse arr[] using for loop from i=0 to i<k.
If (count < N − 1 && height > 1) then increment count for next index and add this node to tree using newNode−>root.push_back(create_tree(arr, N, k, height − 1, count)).
Otherwise end the tree by pushing NULL using newNode−>root.push_back(NULL);
At the end return the pointer to the node.
Function create_tree(int* arr, int N, int k, int count) returns the height of the tree.
Calculate height= (int)ceil(log((double)N * (k − 1) + 1) / log((double)k));
Call create_tree(arr, N, k, height, count) in return statement for tree at height calculated above.
Function postorder_traversal(Tree_Node* node, int k) prints the preorder traversal of the k−ary tree rooted at node.
If the node is NULL then return nothing.
Traverse using for loop from i=0 to i<k and recursively call postorder_traversal(node−>root[i], k);
Print node−>address at the end of for loop.
Example
#include <bits/stdc++.h>
using namespace std;
struct Tree_Node{
int address;
vector<Tree_Node*> root;
};
Tree_Node* new_Node(int data){
Tree_Node* newNode = new Tree_Node;
newNode−>address = data;
return newNode;
}
Tree_Node* create_tree(int arr[], int N, int k, int height, int& count){
if(N <= 0){
return NULL;
}
Tree_Node* newNode = new_Node(arr[count]);
if (newNode == NULL){
cout<<"Code Dumped";
return NULL;
}
for(int i = 0; i < k; i++){
if (count < N − 1 && height > 1){
count++;
newNode−>root.push_back(create_tree(arr, N, k, height − 1, count));
}else{
newNode−>root.push_back(NULL);
}
}
return newNode;
}
Tree_Node* create_tree(int* arr, int N, int k, int count){
int height = (int)ceil(log((double)N * (k − 1) + 1) / log((double)k));
return create_tree(arr, N, k, height, count);
}
void preorder_traversal(Tree_Node* node, int k){
if (node == NULL){
return;
}
for(int i = 0; i < k; i++){
preorder_traversal(node−>root[i], k);
}
cout<<node−>address<< " ";
}
int main(){
int arr[] = {2, 5, 1, 3, 6, 7, 2, 1 };
int size = 8;
int children = 2;
int count = 0;
Tree_Node* node = create_tree(arr, size, children, count);
cout<<"Construct the full k−ary tree from its preorder traversal are: ";
preorder_traversal(node, children);
return 0;
}Output
If we run the above code it will generate the following output −
Construct the full k-ary tree from its preorder traversal are: 3 6 1 2 1 7 5 2
287 Views
To Continue Learning Please Login