
 Data Structure
Data Structure Networking
Networking RDBMS
RDBMS Operating System
Operating System Java
Java MS Excel
MS Excel iOS
iOS HTML
HTML CSS
CSS Android
Android Python
Python C Programming
C Programming C++
C++ C#
C# MongoDB
MongoDB MySQL
MySQL Javascript
Javascript PHP
PHP
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Explain the Hamming Codes in Error Correction
The Hamming code can be used to the data units of any length when we consider the two codewords which have the same length. The Hamming distance between two codewords is represented as the number of positions in which their specific item differs.
Example
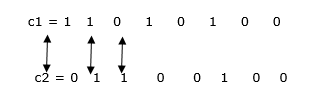
Hamming Distance is 3.
Hamming code is also known as linear block code. The family of (n, k) hamming codes for m is defined.
Block length n=2m-1.
The number of message bits k=2m-m-1.
Number of Parity Bits = n-k=m.
Where m≥3
Minimum distancemin=3.
-
Code rate = Code efficiency = $\frac{k}{n} = \frac{2^{m}-m-1}{2^{m}-1} = 1 - \frac{m}{2^{m}-1}$ of m>> 1
then, code rate r=1 where k is message bits and n is number of transmitted bits per block.
Structure
The parity (redundant) bits are inserted between the data units or the end of data units.
To evaluate, several redundancy bits are needed to accurately represent the given number of data bits m. We should find relationships between m and r.
If a total transmission is m + r, r must indicate m + r + 1 different states. One state defines no error, and m + r states denote the position of an error in each of m + r positions.
Therefore, m + r + 1 states should be discovered by r bits, and r bits can denote 2r multiple states. So 2r ≥m+r+1.
Let us suppose m = 7, then the minimal r-value that satisfies this equation is 4.
| 11 |
10 |
9 |
8 |
7 |
6 |
5 |
4 |
3 |
2 |
1 |
| d |
D |
r4 |
D |
D |
D |
D |
r3 | D |
r2 |
r1 |
In this r bit is put on 2n position. For example, 20 = 1, 21 = 2, 22 = 4 ect positions
In Hamming code, each r bit is VRC (Vertical Redundancy Check).
r1 bit is calculated by using all bit positions whose binary representation contains 1 in the rightmost position, 1, 3, 5, 7, 9, 11.
r2 bit is computed by using all positions with a 1 in 2, 3, 6, 7, 10, 11 positions and so on. r3 bit will take care of bits position at 4, 5, 6. r4 is checked at 8, 9, 10, 11.
Example
1011
11 1001 0111 0101 0011 0001
| d |
D |
D |
r4 |
d |
d |
d |
r3 | d |
r2 |
r1 |
r2 will take care of it
1011 1010
11 10 0111 0110 0111 0010
| d |
D |
D |
r6 |
d |
d |
d |
r4 | d |
r2 |
r1 |
and so on.
Calculate r values
We locate each bit of original characters in its suitable position in the 11-bit unit. We can calculate even parities for the multiple bit combinations. The parity value for each consolidation is the value of the correlating r bit.
Example
is calculated to support the even parity for merging bits 3, 5, 7, 9, 11, etc. The last 11-bit code is sent through the transmitted line.

