Error Correcting Codes - Low-Density Parity Check Codes

Error Correcting Codes

Error-correcting codes (ECC) are a sequence of numbers generated by specific algorithms for detecting and removing errors in data that has been transmitted over noisy channels. Error correcting codes ascertain the exact number of bits that has been corrupted and the location of the corrupted bits, within the limitations in algorithm.

ECCs can be broadly categorized into two types, block codes and convolution codes. Low - density parity check code (LDPC) is a linear error correcting block code. They are suitable for large block sizes in very noisy channels.

LDPC codes were developed by Robert G. Gallager, in his doctoral dissertation at the Massachusetts Institute of Technology in 1960. So, they are also known as Gallager codes.

Encoding by Low-Density Parity Check Codes

A low - density parity check (LFPC) code is specified by a parity-check matrix containing mostly 0s and a low density of 1s. The rows of the matrix represent the equations and the columns represent the bits in the codeword, i.e. code symbols.

A LDPC code is represented by , where is the block length, is the number of 1s in each column and is the number of 1s in each row, holding the following properties −

• j is the small fixed number of 1’s in each column, where j > 3

• k is the small fixed number of 1’s in each row, where k > j.

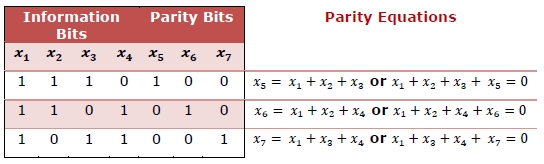
Example 1 − Parity Check Matrix of Hamming Code

The following parity check matrix Hamming code having , with 4 information bits followed by 3 even parity bits. The check digits are diagonally 1. The parity equations are given alongside −

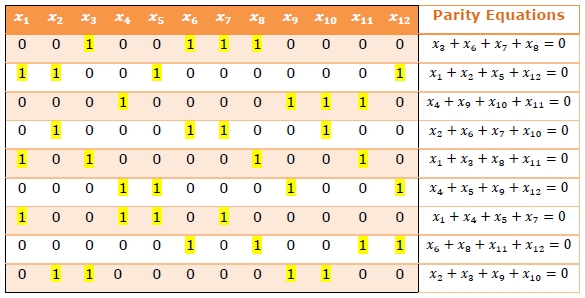
Example 2 − Low - Density Parity Check Matrix

This examples illustrates an (12, 3, 4) LDPC matrix, i.e. n = 12, j = 3 and k = 4. This implies that each equation operates on 4 code symbols and each code symbol appears in 3 equations. Unlike parity check matrix of the Hamming code, this code does not have any diagonal 1s in parity bits.

Decoding of LDPC Codes

There are two possible decoding techniques of LDPC codes −

• In the first technique, the decoder does all the parity checks as per the parity equations. If any bit is contained in more than a fixed number of unsatisfied parity equations, the value of that bit is reversed. Once the new values are obtained, parity equations are recomputed using the new values. The procedure is repeated until all the parity equations are satisfied.

  This decoding procedure is simple and but is applicable only when the parity-check sets are small.

• The second method performs probabilistic algorithms on LDPC graphs. The graph is a sparse bipartite graph that contains two sets of nodes, one set representing the parity equations and the other set representing the code symbols. A line connects node in first set to the second if a code symbol is present in the equation. Decoding is done by passing messages along the lines of the graph. Messages are passed from message nodes to check nodes, and from check nodes back to message nodes and their parity values are calculated.

  The two subclasses of these methods are belief propagation and maximum likelihood decoding. Though these decoding algorithms are complex, they yield better results than the former.