Hamming code for single error correction, double error detection

Hamming code is a block code that is capable of detecting up to two simultaneous bit errors and correcting single-bit errors. It was developed by R.W. Hamming for error correction.

In this coding method, the source encodes the message by inserting redundant bits within the message. These redundant bits are extra bits that are generated and inserted at specific positions in the message itself to enable error detection and correction. When the destination receives this message, it performs recalculations to detect errors and find the bit position that has error.

Hamming Code for Single Error Correction

The procedure for single error correction by Hamming Code includes two parts, encoding at the sender’s end and decoding at receiver’s end.

Encoding a message by Hamming Code

The procedure used by the sender to encode the message encompasses the following steps −

• Step 1 − Calculation of the number of redundant bits.

• Step 2 − Positioning the redundant bits.

• Step 3 − Calculating the values of each redundant bit.

Once the redundant bits are embedded within the message, this is sent to the destination.

Step 1 − Calculation of the number of redundant bits.

If the message contains m number of data bits, r number of redundant bits are added to it so that is able to indicate at least (m + r + 1) different states. Here, (m + r) indicates location of an error in each of bit positions and one additional state indicates no error. Since, r bits can indicate 2^r states, 2^r must be at least equal to (m + r + 1). Thus the following equation should hold −

2^r ≥ 𝑚 + 𝑟 + 1

Example 1 − If the data is of 7 bits, i.e. m = 7, the minimum value of r that will satisfy the above equation is 4, (2⁴ ≥ 7 + 4 + 1). The total number of bits in the encoded message, (m + r) = 11. This is referred as (11,4) code.

Step 2 − Positioning the redundant bits.

The r redundant bits placed at bit positions of powers of 2, i.e. 1, 2, 4, 8, 16 etc. They are referred in the rest of this text as r₁ (at position 1), r₂ (at position 2), r₃ (at position 4), r₄ (at position 8) and so on.

Example 2 − If, m = 7 comes to 4, the positions of the redundant bits are as follows −

Step 3 − Calculating the values of each redundant bit.

The redundant bits are parity bits. A parity bit is an extra bit that makes the number of 1s either even or odd. The two types of parity are −

• Even Parity − Here the total number of bits in the message is made even.

• Odd Parity − Here the total number of bits in the message is made odd.

Each redundant bit, r_i, is calculated as the parity, generally even parity, based upon its bit position. It covers all bit positions whose binary representation includes a 1 in the i^th position except the position of r_i. Thus −

• r₁ is the parity bit for all data bits in positions whose binary representation includes a 1 in the least significant position excluding 1 (3, 5, 7, 9, 11 and so on)

• r₂ is the parity bit for all data bits in positions whose binary representation includes a 1 in the position 2 from right except 2 (3, 6, 7, 10, 11 and so on)

• r₃ is the parity bit for all data bits in positions whose binary representation includes a 1 in the position 3 from right except 4 (5-7, 12-15, 20-23 and so on)

Example 3 − Suppose that the message 1100101 needs to be encoded using even parity Hamming code. Here, m = 7 and r comes to 4. The values of redundant bits will be as follows −

Hence, the message sent will be 11000101100.

Decoding a message in Hamming Code

Once the receiver gets an incoming message, it performs recalculations to detect errors and correct them. The steps for recalculation are −

• Step 1 − Calculation of the number of redundant bits.

• Step 2 − Positioning the redundant bits.

• Step 3 − Parity checking.

• Step 4 − Error detection and correction

Step 1) Calculation of the number of redundant bits

Using the same formula as in encoding, the number of redundant bits are ascertained.

2^r ≥ 𝑚 + 𝑟 + 1

where m is the number of data bits and r is the number of redundant bits.

Step 2) Positioning the redundant bits

The r redundant bits placed at bit positions of powers of 2, i.e. 1, 2, 4, 8, 16 etc.

Step 3) Parity checking

Parity bits are calculated based upon the data bits and the redundant bits using the same rule as during generation of c₁, c₂, c₃, c₄ etc. Thus

c₁ = parity(1, 3, 5, 7, 9, 11 and so on)

c₂ = parity(2, 3, 6, 7, 10, 11 and so on)

c₃ = parity(4-7, 12-15, 20-23 and so on)

Step 4) Error detection and correction

The decimal equivalent of the parity bits binary values is calculated. If it is 0, there is no error. Otherwise, the decimal value gives the bit position which has error. For example, if c₁c₂c₃c₄ = 1001, it implies that the data bit at position 9, decimal equivalent of 1001, has error. The bit is flipped (converted from 0 to 1 or vice versa) to get the correct message.

Example 4 − Suppose that an incoming message 11110101101 is received.

Step 1 − At first the number of redundant bits are calculated using the formula 2^r ≥ m + r + 1. Here, m + r + 1 = 11 + 1 = 12. The minimum value of r such that 2^r ≥ 12 is 4.

Step 2 − The redundant bits are positioned as below −

Step 3 − Even parity checking is done −

c₁ = even_parity(1, 3, 5, 7, 9, 11) = 0

c₂ = even_parity(2, 3, 6, 7, 10, 11) = 0

c₃ = even_parity (4, 5, 6, 7) = 0

c₄ = even_parity (8, 9, 10, 11) = 0

Step 4 - Since the value of the check bits c₁c₂c₃c₄ = 0000 = 0, there are no errors in this message.

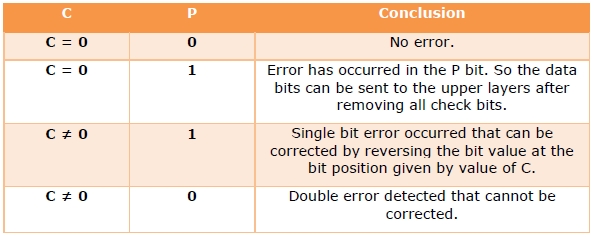
Hamming Code for double error detection

The Hamming code can be modified to correct a single error and detect double errors by adding a parity bit as the MSB, which is the XOR of all other bits.

Example 5 − If we consider the codeword, 11000101100, sent as in example 3, after adding P = XOR(1,1,0,0,0,1,0,1,1,0,0) = 0, the new codeword to be sent will be 011000101100.

At the receiver’s end, error detection is done as shown in the following table −