Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Error Correcting Codes - Reed-Solomon codes
Errors and Error Correcting Codes
Errors in data occur when bits get corrupted in the data. When bits are transmitted over the computer network, they are subject to get corrupted due to interference and network problems, leading to errors.
Error-correcting codes (ECC) are a sequence of numbers generated by specific algorithms for detecting and removing errors in data that has been transmitted over noisy channels. Error correcting codes ascertain the exact number of bits that has been corrupted as well as the location of the corrupted bits, within the limitations in algorithm.
ECCs can be broadly categorized into two types, block codes and convolution codes. Reed - Solomon Code is a type of block code.
Reed - Solomon Code
Reed - Solomon error correcting codes are one of the oldest codes that were introduced in 1960s by Irving S. Reed and Gustave Solomon. It is a subclass of non - binary BCH codes. BCH codes (Bose-Chaudhuri-Hocquenghem codes) are cyclic ECCs that are constructed using polynomials over data blocks.
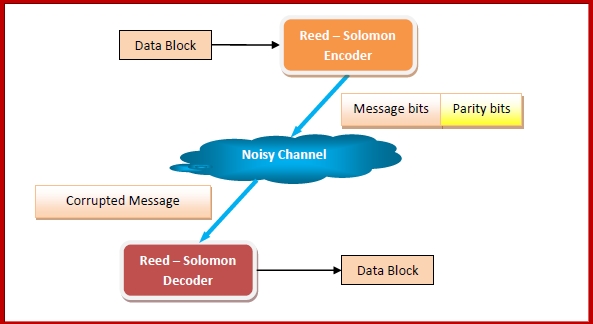
A Reed - Solomon encoder accepts a block of data and adds redundant bits (parity bits) before transmitting it over noisy channels. On receiving the data, a decoder corrects the error depending upon the code characteristics.
Application Areas of Reed-Solomon Codes
The prominent application areas are −
Storage areas like CDs, DVDs, Blu-ray Discs
High speed data transmission technologies such as DSL and WiMAX
High speed modems
QR Codes
Broadcast systems such as satellite communications
Storage systems such as RAID 6
Parameters of Reed - Solomon Codes
A Reed-Solomon code is specified as RS(n,k).
Here, n is the block length which is recognizable by symbols, holding the relation, n = 2m - 1.
The message size is of k bits.
So the parity check size is (n - k) bits
The code can correct up to (t) errors in a codeword, where (2t = n - k).
The following diagram shows a Reed-Solomon codeword −
Generator Polynomial of Reed Solomon Code
In coding systems with block codes, valid code words consists of polynomials that are divisible by another fixed polynomial of short length. This fixed polynomial is called generator polynomial.
In Reed Solomon code, generator polynomial with factors is constructed where each root is a consecutive element in the Galois field. The polynomial is of the form −
g(x) = (x - α) (x - α2) (x - α3) ......(x - α2t)where α is a primitive element.
Encoding using Reed Solomon Code
The method of encoding in Reed Solomon code has the following steps −
The message is represented as a polynomial p(x), and then multiplied with the generator polynomial g(x).
The message vector [x1,x2,x3.....xk] is mapped to a polynomial of degree less than k such that px(αi) = xi for all i = 1,...k
The polynomial is evaluated using interpolation methods like Lagrange Interpolation.
Using this polynomial, the other points αk + 1....αn, are evaluated.
The encoded message is calculated as s(x) = p(x) * g(x). The sender sends this encoded message along with the generator polynomial g(x).
Decoding using Reed Solomon Code
At the receiving end, the following decoding procedure done −
The receiver receives the message r(x) and divides it by the generator polynomial g(x).
If r(x)/g(x)=0, then it implies no error.
If r(x)/g(x)≠0, then the error polynomial is evaluated using the expression: r(x) = p(x) * g(x) + e(x)
The error polynomial gives the error positions.
4K+ Views
