Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Error Correcting Codes - Binary Convolutional Code
Errors and Error Correcting Codes
Errors occurs when bits get corrupted while transmission over the computer network, due to interference and network problems.
Error-correcting codes (ECC) are a sequence of numbers generated by specific algorithms for detecting and removing errors in data that has been transmitted over noisy channels. Error correcting codes ascertain the exact number of bits that has been corrupted and the location of the corrupted bits, within the limitations in algorithm.
ECCs can be broadly categorized into two types, block codes and convolution codes.
Binary Convolutional Codes
In convolutional codes, the message comprises of data streams of arbitrary length and a sequence of output bits are generated by the sliding application of Boolean functions to the data stream.
In block codes, the data comprises of a block of data of a definite length. However, in convolutional codes, the input data bits are not divided into block but are instead fed as streams of data bits, which convolve to output bits based upon the logic function of the encoder. Also, unlike block codes, where the output codeword is dependent only on the present inputs, in convolutional codes, output stream depends not only the present input bits but also only previous input bits stored in memory.
Convolutional codes were first introduced in 1955, by Elias. After that, there were many interim researches by many mathematicians. In 1973, Viterbi developed an algorithm for maximum likelihood decoding scheme, called Viterbi scheme that lead to modern convolutional codes.
Encoding by Convolutional Codes
For generating a convolutional code, the information is passed sequentially through a linear finite-state shift register. The shift register comprises of (-bit) stages and Boolean function generators.
A convolutional code can be represented as (n,k, K) where
k is the number of bits shifted into the encoder at one time. Generally, k = 1.
n is the number of encoder output bits corresponding to k information bits.
The code-rate, Rc = k/n .
The encoder memory, a shift register of size k, is the constraint length.
n is a function of the present input bits and the contents of K.
The state of the encoder is given by the value of (K - 1) bits.
Example of Generating a Convolutional Code
Let us consider a convolutional encoder with k = 1, n = 2 and K = 3.
The code-rate, Rc = k/n = 1/2 .
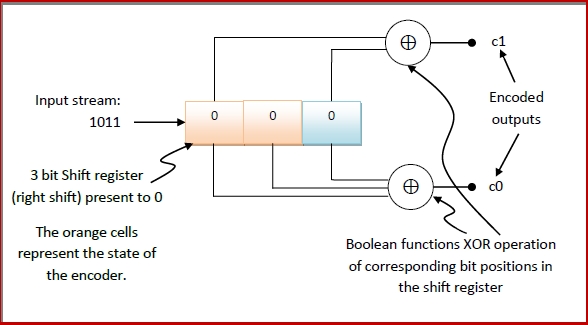
The input string is streamed from right to left into the encoder.
When the first bit, 1, is streamed in the encoder, the contents of encoder will be −
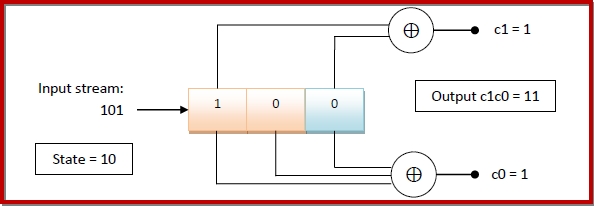
When the next bit, 1 is streamed in the encoder, the contents of encoder will be −
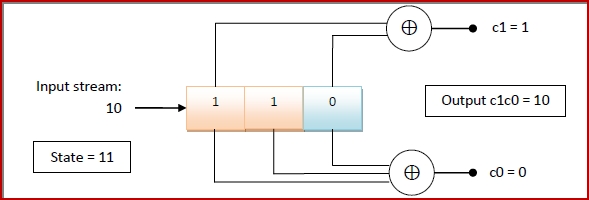
When the next bit, 0 is streamed in the encoder, the contents of encoder will be −
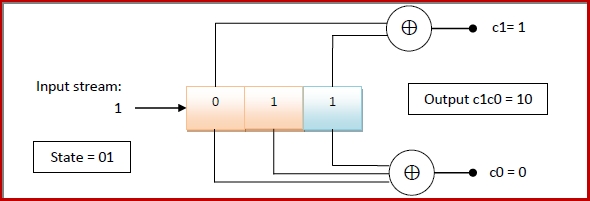
When the last bit, 1 is streamed in the encoder, the contents of encoder will be −
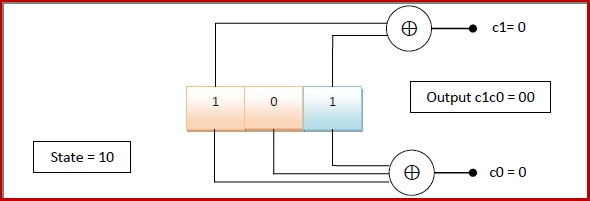
Representing Convolution Encoder with State Transition Diagram and State Table
From the above example, we can see that any particular binary convolutional encoder is associated with a set of binary inputs, a set of binary outputs and a set of states. The transitions and the output may be effectively represented by a state transition diagram and a state table.
For the binary convolution encoder given in the example −
The set of inputs = {0, 1}
The set of outputs = { 00, 10, 11}
The set of states = { 00, 01, 10, 11}We can see that in the initial state, 00, when the input 1 was given, the next state became 10 and the corresponding output was 11. In this state 10, when the input 1 was given, the next state was 11 and the encoder outputs were 10. In the same manner we get the other transitions. When this is tabulated, we get the state transition table as follows −
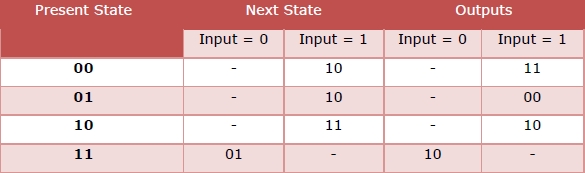
The corresponding state transition diagram will be −
8K+ Views
