Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
What is Error Correction?
In the detection method, only the error can be detected. Still, in the error correction method, the errors are corrected automatically at the receiver end and no need for re-transmission. The burst error correction is very limited to 2 bits only.
Each kbit block of data is added with redundant bits that make a codeword of n bits (n > k). A forward error correction encoder is used on the transmission end. Then, the codeword is transmitted. The signal is demodulated to make a bit string equivalent to the initial codeword to include the errors at the receiver.
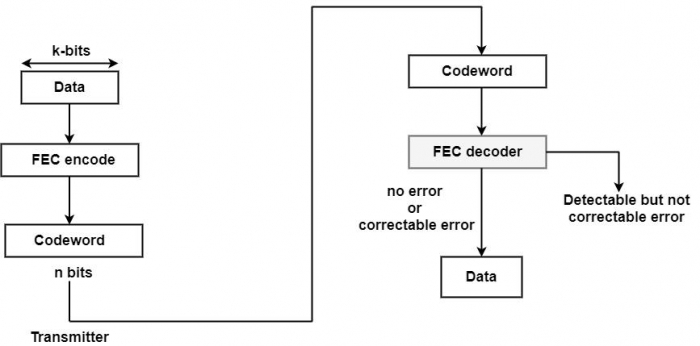
If no bit error, the FEC decoder output = original codeword and produced original data.
As a specific error design, it is feasible for the decoder to identify and upgrade the errors. FEC decoder is capable of mapping this block into original data.
For specific error, the decoder can identify but not upgrade error. It is reported as an unmanageable error.
Example
Suppose, a Hamming code is used to identify and correct the single-bit errors by considering each codeword included in a seven-bit data area such as an ASCII character.
For example, in coding design needed checking bits since, with this design, the check bits appear in all bits locations that are the power of 2. Therefore, this code is called a (1, 7) block code.
For example, the bit location of the value 1001101 are as follows −
| Bit Position | 11 | 10 | 9 | 8 | 7 | 6 | 5 | 4 | 3 | 2 | 1 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Bit Value | 1 | 0 | 0 | x | 1 | 1 | 0 | x | 1 | X | x |
The four-bit location is apparent with x. It can be used for the check bits, which are assumed as follows. The four-bit binary numbers correlating to those fit positions have a binary 1. They are inserted together by using modulo 2 arithmetic, and the four check bits are then the four-bit sum.
11 = 1011 7 = 0111 6 = 0110 3 = 0011 1011
Thus, the transmitted codeword is as follows −
| Bit Position | 11 | 10 | 9 | 8 | 7 | 6 | 5 | 4 | 3 | 2 | 1 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Bit Value | 1 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | 1 | 0 | 1 |
Similarly, at the receiver, the four-bit binary numbers correlating to those have the positions with a binary 1. It is used to check bits. They are again inserted together and if no errors appear, the modulo 2 sum should be zero.
11 = 1101
8 = 1101
7 = 0111
6 = 0110
3 = 0011
1 = 0001
0000Suppose a single-bit error. It can say bit 11 is corrupted from 1 to 0. The new modulo 2 sum would be as follows −
8 = 1000 7 = 0111 6 = 0110 3 = 0011 1 = 0001 0 = 1011
Firstly, the sum is non-zero, which indicates an error.
Secondly, the modulo 2 sum is equivalent to decimal 11 and suggests that bit 11 is erroneous bits.
544 Views
