
- CUDA - Home
- CUDA - Introduction
- CUDA - Introduction to the GPU
- Fixed Functioning Graphics Pipelines
- CUDA - Key Concepts
- Keywords and Thread Organization
- CUDA - Installation
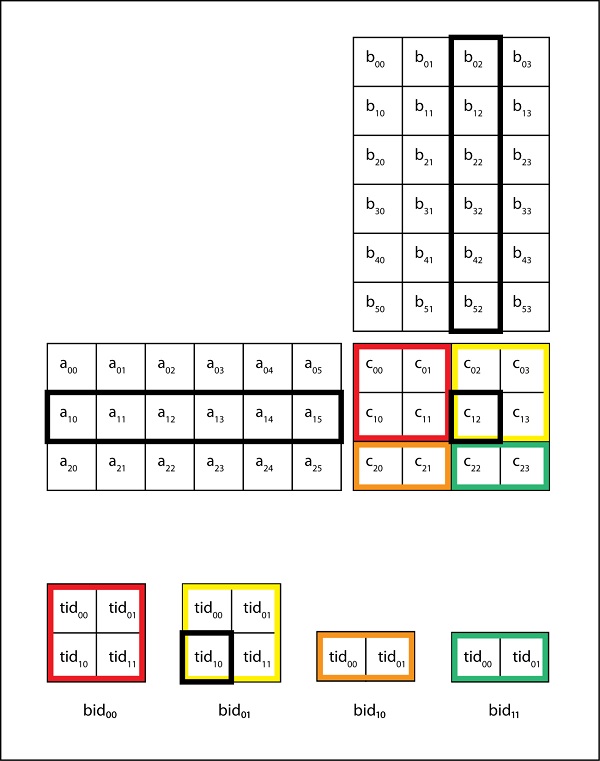
- CUDA - Matrix Multiplication
- CUDA - Threads
- CUDA - Performance Considerations
- CUDA - Memories
- CUDA - Memory Considerations
- Reducing Global Memory Traffic
- CUDA - Caches
CUDA - Reducing Global Memory Traffic
Resources in SM are dynamically partitioned and assigned to threads to support their execution. As has been explained in the previous chapter, the number of resources in SM are limited, and the higher the demands of a thread, the lower the number of threads that can actually run parallel inside the SM. Execution resources of SM include registers, shared memory, thread block slots and thread slots.
In the previous chapter, It has already been discussed that the current generation of CUDA devices support upto 1536 thread slots. That is, each SM can support no more than 1536 threads that can run in parallel. It has to be remembered that there is no capping on the number of thread blocks that can occupy a SM. They can be as many as would keep the total number of threads less than or equal to 1536 per SM. For example, there may be 3 blocks of 512 threads each, or 6 blocks of 256 threads each, or 12 blocks of 128 threads each.
This ability of CUDA to dynamically partition SM resources into thread blocks makes it the real deal. Fixed partitioning methods, in which each thread block receives a fixed number of execution resources regardless of its need leads to wasting of execution resources, which is not desired, as they are already at a premium. Dynamics partition has its own nuances. For example, suppose each thread block has 128 threads. This way, each SM will have 12 blocks. But we know that the current generation of CUDA devices support no more than 8 thread block slots per SM. Thus, out of 12, only 8 blocks will be allowed. This means that out of 1536 threads, only 1024 will be allocated to the SM. Thus, to fully utilize the available resources, we need to have at least 256 threads in each block.
In the matrix-multiplication example, consider that each SM has 16384 registers and each thread requires 10 registers. If we have 16x16 thread blocks, how many registers can run on each SM? The total number of registers needed per thread block = 256x10 = 2560 registers. This means that a maximum of 6 thread blocks (that need 15360 registers) can execute in a SM.
Thus, each SM can have a maximum of 6 x 256=1536 threads run on each SM. What if the number of registers required by each thread is 12? In that case, a thread block requires 256 x 12 = 3072 registers. Thus, we can have 5 blocks at maximum. This concludes that the maximum number of threads that can be allocated to a SM are 5 x 256 =1280.
It is to be noted that by using just two registers per thread extra, the warp parallelism reduces by 1/6.This is known as performance cliff and refers to a situation in which increasing the resource usage per thread even slightly leads to a large reduction in performance. The CUDA occupancy calculator (a program from Nvidia) can calculate the occupancy of each SM.
Reducing Traffic to the Global Memory Using Tiles
Let us consider an example of matrix-matrix multiplication once again. Our aim is to reduce the number of accesses to global memory to increase arithmetic intensity of the kernel. Let d_N and d_M be of dimensions 4 x 4 and let each block be of dimensions 2 x 2. This implies that, each block is made up of 4 threads, and we require 4 blocks to compute all the elements of d_P.
The following table shows us the memory access pattern of block (0,0) in our previous kernel.
| Thread (0,0) | M0,0 * N0,0 | M0,1 * N1,0 | M0,2 * N2,0 | M0,3 * N3,0 |
| Thread (0,1) | M0,0 * N0,1 | M0,1 * N1,1 | M0,2 * N2,1 | M0,3 * N3,1 |
| Thread (1,0) | M1,0 * N0,0 | M1,1 * N1,0 | M1,2 * N2,0 | M1,3 * N3,0 |
| Thread (1,1) | M1,0 * N0,1 | M1,1 * N1,1 | M1,2 * N2,1 | M1,3 * N3,1 |
From the above figure, we see that both thread (0,0) and thread (1,0) access N1,0. Similarly, both thread (0,0) and thread (0,1) access element M0,0. In fact, each d_M and d_N element is accessed twice during the execution of block (0,0). Accessing the global memory twice for fetching the same data is inefficient. Is it possible to somehow make a thread collaborate with others so that they dont access previously fetched elements? It was explained in the previous chapter that shared memory can be used for inter-thread communication.
Tiled Matrix-Matrix Multiplication
It is an algorithm for matrix multiplication in which threads collaborate to reduce global memory traffic. Using this algorithm, multiple accesses to the global memory for fetching the same data is avoided.
Threads collaboratively load M and N elements into shared memory before using them in calculations.
d_M and d_N are divided into small tiles. Let the tile dimension be equal to the block dimension. In our example, each time has dimensions 2 x 2.
The dot product done by each thread is divided into multiple phases. During each phase, all threads in a block collaboratively load two tiles into the shared memory. Let us call these tiles Mds and Nds.
The following figure illustrates the above mentioned points −


In the above figure, in phase one, threads of block (0,0) (other blocks will have similar behaviour) load two tiles, Mds and Nds into the shared memory. Each tile is of size 2 x 2. After the values are loaded into the shared memory, they are used in the calculation of dot product.
The calculation of dot product is done in two phases (P1 and P2 in the above diagram). After phase 2 is over, we get the final value of each element of d_P.
The number of phases required to calculate d_P is equal to N/tile_width, where N is the width of the input matrices. Mds and Nds are reused in each phase.
It should be noted that each value in the shared memory is read twice. In this way, we reduce the number of access to global memory by half. As a rule, for a tile of size N x N, the number of access to the global memory is reduced by a factor of N.
__global__ void MatrixMulKernel(float* d_M, float* d_N, float* d_P, int Width) {
__shared__ float Mds[TILE_WIDTH][TILE_WIDTH];
__shared__ float Nds[TILE_WIDTH][TILE_WIDTH];
int bx = blockIdx.x;
int by = blockIdx.y;
int tx = threadIdx.x;
int ty = threadIdx.y;
int Row = by * TILE_WIDTH + ty;
int Col = bx * TILE_WIDTH + tx;
float Pvalue = 0;
for (int m = 0; m < Width/TILE_WIDTH;m++) {
Mds[ty][tx] = d_M[Row*Width + m*TILE_WIDTH + tx];
Nds[ty][tx] = d_N[(m*TILE_WIDTH + ty)*Width + Col];
__syncthreads(); //Wait till all the threads have finished loading elements into the tiles.
for (int k = 0; k < TILE_WIDTH;k++) {
Pvalue += Mds[ty][k] * Nds[k][tx];
__syncthreads();
}
d_P[Row*Width + Col] = Pvalue;
}
}