
- Cosmology - Home
- The Expanding Universe
- Cepheid Variables
- Redshift and Recessional Velocity
- Redshift Vs. Kinematic Doppler Shift
- Cosmological Metric & Expansion
- Robertson-Walker Metric
- Hubble Parameter & Scale Factor
- Friedmann Equation & World Models
- Fluid Equation
- Matter Dominated Universe
- Radiation Dominated Universe
- The Dark Energy
- Spiral Galaxy Rotation Curves
- Velocity Dispersion Measurements of Galaxies
- Hubble & Density Parameter
- Age of The Universe
- Angular Diameter Distance
- Luminosity Distance
- Type 1A Supernovae
- Cosmic Microwave Background
- CMB - Temperature at Decoupling
- Anisotropy of CMB Radiation & Cobe
- Modelling the CMB Anisotropies
- Horizon Length at the Surface of Last Scattering
- Extrasolar Planet Detection
- Radial Velocity Method
- Transit Method
- Exoplanet Properties
Cosmology - Robertson-Walker Metric
In this chapter, we will understand in detail regarding the Robertson-Walker Metric.
Model for Scale Factor Changing with Time
Suppose a photon is emitted from a distant galaxy. The space is forward for photon in all directions. The expansion of the universe is in all the directions. Let us see how the scale factor changes with time in the following steps.
Step 1 − For a static universe, the scale factor is 1, i.e. the value of comoving distance is the distance between the objects.
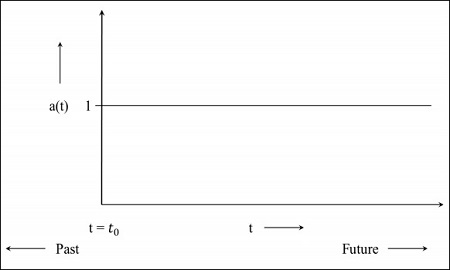
Step 2 − The following image is the graph of the universe that is still expanding but at a diminishing rate, which means the graph will start in the past. The t = 0 indicates that the universe started from that point.
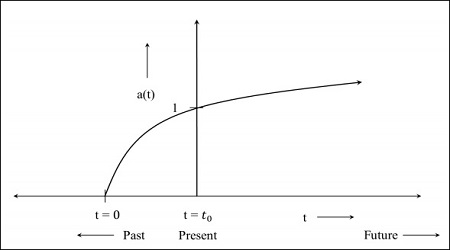
Step 3 − The following image is the graph for the universe which is expanding at a faster rate.
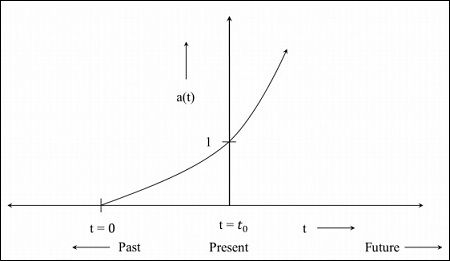
Step 4 − The following image is the graph for the universe that starts contracting from now.
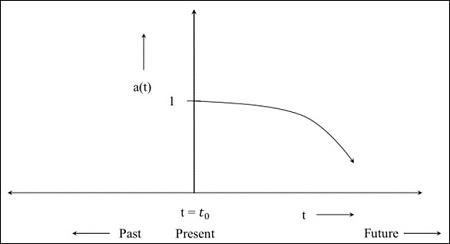
If the value of the scale factor becomes 0 during the contraction of universe, it implies the distance between the objects becomes 0, i.e. the proper distance becomes 0. The comoving distance which is the distance between the objects at a present universe, is a constant quantity. In the future, when the scale factor becomes 0, everything will come closer. The model depends on the component of the universe.
The Metric for flat (Euclidean: there is no parameter for curvature) expanding universe is given as −
$$ds^2 = a^2(t)\left ( dr^2+r^2d\theta^2+r^2sin^2\theta d\varphi^2 \right )$$
For spacetime, the line element that we obtained in the above equation is modified as −
$$ds^2 = c^2dt^2 - \left \{ a^2(t) \left ( dr^2 + r^2d\theta ^2 + r^2sin^2\theta d\varphi^2 \right ) \right \}$$
For space time, the time at which the photon is emitted and when it is detected is different. The proper distance is the instantaneous distance to objects which can change over time due to the expansion of the universe. It is the distance that the photon had travelled from different objects to get to us. It is related to the comoving distance as −
$$d_p = a(t) \times d_c$$
where $d_p$ is the proper distance and $d_c$ is the comoving distance, which is fixed.
The distance measured to the objects in the present universe is taken as the comoving distance, which means the comoving distance is fixed and is unchanged by the expansion. For past, the scale factor was less than 1, which indicates that the proper distance was smaller.
We can measure the redshift to a galaxy. Hence the proper distance $d_p$ corresponds to $c \times t(z)$, where $t(z)$ is the lookback time towards a redshift and c is the speed of light in vacuum. The lookback time is a function of the redshift (z).
Based on the above notion, let us analyze how cosmological red shift is interpreted in this scenario of $d_p = a(t) \times d_c$.
Assume a photon (which is earth bound) is emitted by the galaxy, G. The $t_{em}$ corresponds to the time when photon was emitted; $a(t_{em})$ was the scale factor at that time when the photon was emitted. By the time of detection of the photon, the whole universe had expanded, i.e. the photon is redshifted at the time of detection. The $t_{obs}$ corresponds to the time when the photon is detected and the corresponding scale factor is $a(t_{obs})$.
The factor by which the universe has grown is given by −
$$\frac{a(t_{obs})}{a(t_{em})}$$
The factor by which wavelength has expanded is −
$$\frac{\lambda_{obs}}{\lambda_{em}}$$
which is equal to the factor by which the universe has grown. The symbols have their usual meaning. Therefore,
$$\frac{a(t_{obs})}{a(t_{em})} = \frac{\lambda_{obs}}{\lambda_{em}}$$
We know that redshift (z) is −
$$z=\frac{\lambda_{obs} - \lambda_{em}}{\lambda_{em}} = \frac{\lambda_{obs}}{\lambda_{em}} - 1$$
$$1 + z = \frac{a(t_{obs})}{a(t_{em})}$$
The present value of the scale factor is 1, hence $a(t_{obs}) = 1$ and denoting the scale factor when photon was emitted in the past by $a(t)$.
Therefore,
$$1 + z = \frac{1}{a(t)}$$
Interpretation of Redshift in Cosmology
To understand this, let us take the following example: If $z = 2$ then $a(t) = 1/3$.
It implies that the universe has expanded by a factor of three since light left that object. The wavelength of the received radiation has expanded by a factor of three because the space has expanded by the same factor during its transit from the emitting object. It should be noted that at such large values of z, the redshift is mainly the cosmological redshift, and it is not a valid measure of the actual recessional velocity of the object with respect to us.
For cosmic microwave background (CMB), z = 1089, which means that the present universe has expanded by a factor of ∼1090. The metric for flat, Euclidean, expanding universe is given as −
$$ds^2 = a^2(t)(dr^2 + r^2d\theta^2 + r^2sin^2\theta d\varphi^2)$$
We wish to write the metric in any curvature.
Robertson and Walker proved for any curvature universe (which is homogeneous and isotropic), the metric is given as −
$$ds^2 = a^2(t) \left [ \frac{dr^2}{1-kr^2} + r^2d\theta^2 + r^2sin^2\theta d\varphi^2 \right ]$$
This is generally known as the RobertsonWalker Metric and is true for any topology of space. Please note the extra factor in $dr^2$. Here is the curvature constant.
Geometry of the Universe
The Geometry of the Universe is explained with the help of the following Curvatures, which include −
- Positive Curvature
- Negative Curvature
- Zero Curvature
Let us understand each of these in detail.
Positive Curvature
If a tangent plane drawn at any point on the surface of the curvature does not intersect at any point on the surface, it is called surface with a positive curvature i.e. the surface stays on one side of the tangent plane at that point. The surface of the sphere has positive curvature.
Negative Curvature
If a tangent plane drawn at a point on the surface of the curvature intersects at any point on the surface, it is called as a surface with a negative curvature i.e., the surface curves away from the tangent plane in two different directions. A saddle-shaped surface has a negative curvature.
Now consider the surface of a sphere. If a triangle is constructed on the surface of the sphere by joining three points with geodesic (arc of great circles), the sum of the interior angles of the spherical triangle is greater than 180o, i.e. −
$$\alpha + \beta + \gamma > \pi$$
Such spaces are called positively curved spaces. Also, the curvature is homogeneous and isotropic. In general, the angle at the vertices of the spherical triangle follows the relation −
$$\alpha + \beta +\gamma = \pi + A/R^2$$
where A is the area of the triangle and R is the radius of the sphere. The following image depicts a positively curved space.
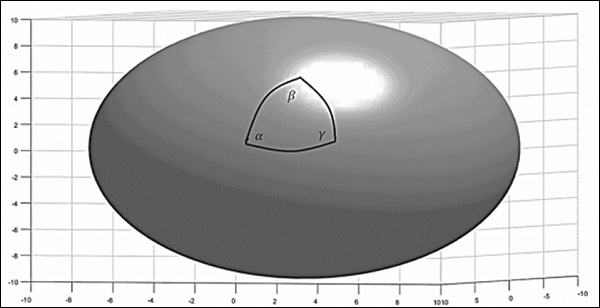
For a positive curvature, the parallel lines should meet. Consider the surface of the earth, which is a positively curved space. Take two starting points on the equator. The lines which cross the equator at right angles are known as the lines of longitude. Since these lines cross the equator at right angles, they can be referred to as parallel lines. Starting from the equator, they eventually intersect at the poles. This method was used by Carl Gauss and others to understand the topology of the earth.
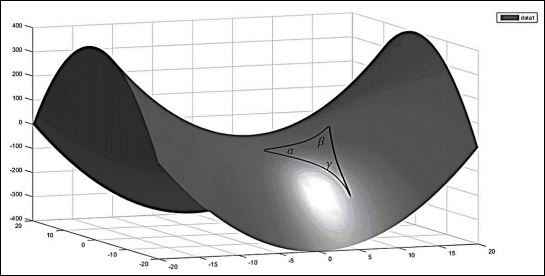
Consider a negatively curved space (a saddle shown in the following image), the sum of interior angles of the triangle is less than 180o, i.e. −
$$\alpha + \beta + \gamma < \pi$$
The angle at the vertices follows the relation −
$$\alpha + \beta + \gamma = \pi - A/R^2$$
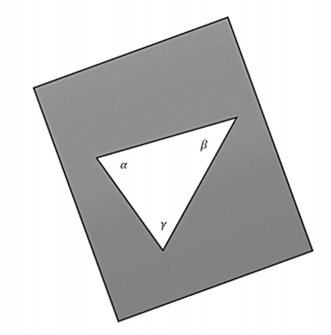
Zero Curvature
A plane surface has zero curvature. Now for a flat space, if a plane is taken and a triangle is constructed by joining three points with geodesic (straight lines), the interior sum of angles will be −
$$\alpha + \beta + \gamma = \pi$$
The following image is a flat 2-dimensional space.
If one wants a space to be homogeneous and isotropic, only three possibilities remain: the space can be uniformly flat or it can have a uniform positive curvature or it can have a uniform negative curvature.
The curvature constant can assume any of the following three values.
$$k = \begin{cases}+1, & for \: a\: positively \: curved\: space;\\\quad 0, & for\: a \: flat \: space;\\-1, & for\: a \: negatively \: curved \: space;\end{cases}$$
Global Topology of the Universe
The universe has a certain topology, but locally it can have wrinkles. Depending on how the matter is distributed in the space, there are smaller variations in the curvature. Let us assume that there is a class of objects which have the same true size no matter where it is in the universe, which means they are like standard candles. They dont have the same brightness, but they have the same size.
If the object is in positively curved space and photons comes from point A (one end of the object) and B (other end of the object), the photons will propagate parallel in positively curved space through the path of geodesic and they will eventually meet. For an observer at C, it will seem that it came from two different points in different directions.
If the object is in the local universe and we measure the angular size, it is not affected by the curvature. If the same class of object is seen at a greater redshift, the angular size does not correlate with.
$$\theta = \frac{d}{r}$$
Where d is the size of the object and r is the distance to the object, i.e. if size is greater than the local size, it means the curvature is positive. The following image is a representation of the photon detected in a positively curved space.
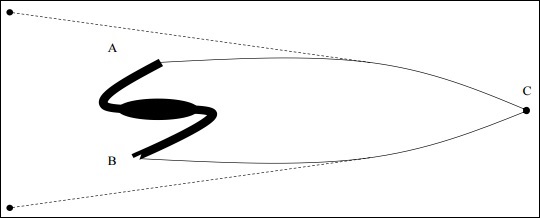
It is to be noted that there is no real astrophysical object which is of standard size and morphology. Although a massive elliptical cD galaxies were thought to fit the standard candles, but they were also found to be evolving with time.
Finding Distances to Galaxies
In this section, we will discuss how to find the distance to a galaxy by taking into consideration the following image.
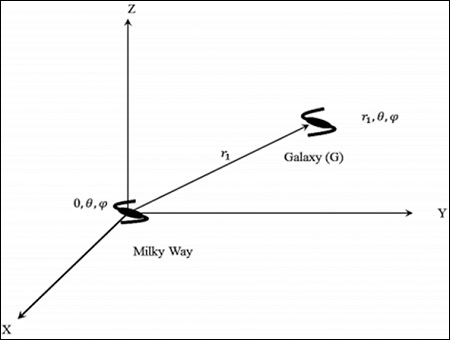
Consider the Milky Way at (r, θ,) in a cosmological rest frame. One can take = 0; (0, θ,ϕ), i.e. the centre of the universe by invoking the assumption of homogeneity.
Consider a galaxy G at (r1, θ,). The distance (proper) is the shortest radial distance travelled by a photon. From the symmetry of space time, the null geodesic from r = 0 to r = r1, has a constant direction in space. In its radial propagation, the angular co-ordinates do not change. If angular coordinates get changed, then it is not the shortest path. That is the reason why the curvature term is present in dr2.
Points to Remember
The expansion of the universe is in all the directions.
The universe can be static, expanding or contracting depending upon the scale factor evolution.
The cD-galaxies evolve with time and hence cannot be used as standard candles.
The universe has certain topology, but locally it can have wrinkles.