Cosmology - Dark Energy

The area of Dark Energy is a very grey area in astronomy because it is a free parameter in all equations, but there is no clear idea what exactly this is.

We will start with the Friedmann’s equations,

$$\left ( \frac{\dot{a}}{a} \right)^2 = \frac{8\pi G}{3}\rho - \frac{k \ast c^2}{a^2}$$

Most of the elementary books on cosmology, they all start with describing the dark energy from this episode that before Hubble’s observation, the universe is closed and static.

Now, for the universe to be static in the right side, both the terms should match and they should be zero, but if the first term is greater than the second term, then the universe will not be static, so Einstein dropped the free parameter ∧ into the field equation to make the universe static, so he argued that no matter what the first term is compared to the second term, you can always get a static universe if there is one more component in the equation, which can compensate the dis-match between these two terms.

$$\left ( \frac{\dot{a}}{a} \right )^2 = \frac{8\pi G}{3}\rho - \frac{k \ast c^2}{a^2} + \frac{\wedge}{3}$$

$$\left ( \frac{\ddot{a}}{a} \right ) = -\frac{4 \pi G}{3}\left ( \rho + \frac{3P}{c^2} \right ) + \frac{\wedge}{3}$$

Where $P = \rho \ast c^2/3$ and $\wedge = \rho \ast c^2$ is the Cosmological Parameter. (Negative sign is only because of attraction)

In the above equation (acceleration equation) −

  • $3P/c^2$ is the negative pressure due to radiation,

  • $-4\pi G/3$ is the attraction due to gravity, and

  • $\wedge/3$ makes a positive contribution.

The third term acts as a repulsive force because another part of the equation is attractive.

The physical significance of the equation is that ˙a = 0 because there was not any evidence which shows that the universe is expanding. What if these two terms are not matching with each other, so it is better to add a component and depending on the offset we can always change the value of the free parameter.

That time there was no physical explanation about this cosmological parameters, which is why when the explanation of the expanding universe was discovered in 1920s, where Einstein immediately had to throw this constant out.

The explanation of this cosmological constant is still in use because it explains a different version of the universe, but the definition of this cosmological constant, the way of interpretation kept changing with time.

Now the concept of this cosmological constant has been brought back to cosmology for many reasons. One of the reason is that, we have observations for energy density of different components of the universe (baryonic, dark matter, radiation), so we know that what this parameter is. Independent observations using cosmic microwave background shows that k=0.

$$CMB, k=0\: \rho = \rho_c = \frac{3H_0^2}{8\pi G} \approx 10 \: Hydrogen \: atoms.m^{-3}$$

For k to be 0, $\rho$ should be equal to $\rho_c$, but everything we know if we add it up that does not give 0, which means that there is some other component that shows that it is much less than $\rho_c$.

$$\rho = \rho_b + \rho_{DM} + \rho_{rad} << \rho_c$$

One more evidence of dark energy comes from the Type 1 Supernova Observation which occurs when white dwarf accretes the matter and exceeds the Chandrashekhar limit, which is a very precise limit (≈ 1.4M). Now every time when Type 1 Supernova Explosion occurs, we have the same mass which means that the total binding energy of the system is same and the amount of light energy we can see is the same.

Of course, the supernova light increases and then faints, but if you measure the peak brightness it is always going to be the same which makes it a standard candidate. So, with a Type 1 Supernova we used to measure the cosmological component of the universe and astronomers found that the supernova with high red shift is 30% − 40% fainter than the low red shift supernova and it can be explained if there is any non-zero ∧ term.

In cosmological models DE (Dark Energy) is treated as a fluid, which means that we can write the equation of state for it. The equation of state is the equation which connects the variables like Pressure, Density, Temperature, and Volume of two different states of the matter.

Dimensionally we see,

$$\frac{8 \pi G}{3}\rho = \frac{\wedge}{3}$$

$$\rho_\wedge = \frac{\wedge}{8\pi G}$$

Energy density of DE,

$$\epsilon_\wedge = \rho_\wedge \ast c^2 = \frac{\wedge c^2}{8 \pi G}$$

Dark energy density parameter,

$$\Omega_\wedge = \frac{\rho_\wedge}{\rho_c}$$

$\Omega_\wedge$ is the density of dark energy in terms of critical density.

$$\rho = \rho_b + \rho_{DM} +\rho_\wedge$$

There are a number of theories about dark energy, which is repelling the universe and causing the universe to expand. One hypothesis is that this dark energy could be a vacuum energy density. Suppose the space itself is processing some energy and when you count the amount of baryonic matter, dark matter and the radiation within the unit volume of space, you are also counting the amount of energy which is associated with the space, but it is not clear that the dark energy is really a vacuum energy density.

We know that the relationship between density and scale factor for dark matter and radiation are,

$$\rho_m \propto \frac{1}{a^3}$$

$$\rho_m \propto \frac{1}{a^4}$$

We have the density v/s scale factor plot. In the same plot, we can see that $\rho_\wedge$ is a constant with the expansion of the universe which does not depend on the scale factor.

The following image shows the relationship between density and the scale factor.

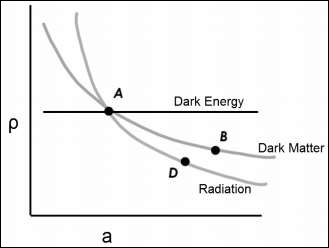
Density Scale Factor

‘ρ’ v/s ‘a’ (scale factor which is related to time) in the same graph, the dark energy is modelled as a constant. So, whatever dark energy we measure in the present universe, it is a constant.

Points to Remember

  • Independent observations using cosmic microwave background shows that k=0.

  • $\rho_\wedge$ is a constant with the expansion of the universe which does not depend on the scale factor.

  • Gravity is also changing with time which is called modified Newtonian dynamics.

Advertisements