Cosmology - Radiation Dominated Universe

In this chapter, we will discuss the Solutions to Friedmann Equations relating to the Radiation Dominated Universe. In the beginning, we compare the energy density of matter to that of radiation. This will enable us to see if our universe is matter dominated or radiation dominated.

Energy Density of Radiation

Radiation prevalent in the present universe can be attributed very little to the stellar sources, but it is mainly due to the remnant CMB (Cosmic Microwave Background).

The energy density of the radiation, $\epsilon_{\gamma,0}$, can be expressed as follows −

$$\epsilon_{\gamma,0} = aT_0^4$$

Here, a is the radiation constant which has the expression $(8\pi^5k_B^4)/(15h^3c^2)$ equal to a = 7.5657 × 10−15erg\: cm−3 K−4. The Temperature, T0, we consider here, corresponds to that of the black body corresponding to the CMB.

Substituting the results, we have,

$$\epsilon_{\gamma,0} = aT_0^4 = 4 \times 10^{-13}erg\: cm^{-3}$$

Energy Density of Matter

In the following calculations, we have the assumption of working with a flat universe and K = 0. We consider the energy density of matter as $\epsilon = \rho c^2$. We consider the following −

$$\rho_{m,0}c^2 = 0.3\rho_{c,0}c^2 = 0.3 \times \frac{3H_0^2}{8\pi G} \times c^2$$

$$\rho_{m,0}c^2 \simeq 2 \times 10^{-8} erg \:cm^{-3}$$

$$\rho_{b,0}c^2 = 0.03\rho_{c,0}c^2 = 0.03 \times \frac{3H_0^2}{8\pi G} \times c^2$$

$$\rho_{b,0}c^2 \simeq 2 \times 10^{-9} erg\: cm^{-3}$$

Thus, from the above calculation, we see that we live in a matter-dominated universe. This can be supported by the fact that the CMB is very cold. As we look back in time, we would have the CMB temperature getting hotter, and will be able to conclude that there might have been an epoch where the universe was dominated by radiation.

Variation of Density and Scale Factor

The fluid equation shows us that −

$$\dot{\rho} + 3\frac{\dot{a}}{a}\left ( \rho + \frac{P}{c^2} \right ) = 0$$

If we consider a dusty universe, we would have P = 0. Setting aside the previous results, we consider the universe as dominated by radiation.

$$\dot{\rho}_{rad} + 3 \frac{\dot{a}}{a}\left ( \rho_{rad} + \frac{P}{c^2} \right ) = 0$$

Using the pressure relation of $P_{rad} = \rho c^{2/3}$ we have −

$$\dot{\rho}_{rad} + 3 \frac{\dot{a}}{a}\left ( \rho_{rad} + \frac{\rho_{rad}}{3} \right ) = 0$$

$$\dot{\rho}_{rad} + 4\frac{\dot{a}}{a}(\rho_{rad}) = 0$$

On further simplification, we have,

$$\frac{1}{a^4}\frac{\mathrm{d}}{\mathrm{d} t}(\rho_{rad}a^4) = 0$$

$$\rho_{rad}a^4 =\: constant$$

$$\rho_{rad} \propto \frac{1}{a^4}$$

The above result shows an inverse 4th power variation of a with $\rho$.

This can be physically interpreted as $a^{-3}$ coming in from the variation in volume as it increases. The remaining $a^{-1}$ can be treated as the energy lost by the photon due to the expansion of space in the universe (Cosmological redshift 1 + z = a-1).

The following image shows the variation of matter and radiation density with time.

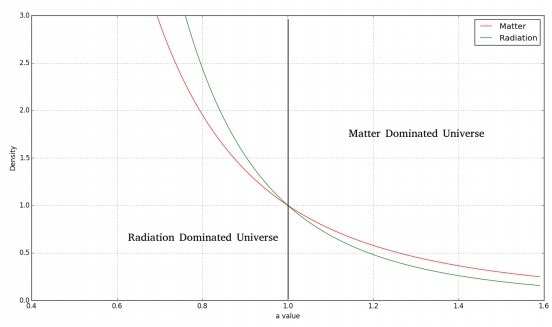
Flat Dominated

For a flat, radiation dominated universe, we would have the Friedmann equation as follows −

$$\left ( \frac{\dot{a}}{a} \right )^2 = \frac{8\pi G\rho}{3}$$

$$\left ( \frac{\dot{a}}{a} \right)^2 = \frac{8\pi G}{3}\frac{\rho_0}{a^4}$$

On simplification and applying the solution to the differential equation, we have −

$$(\dot{a})^2 = \frac{8\pi G\rho_0}{3a^2}$$

$$\Rightarrow a(t) \propto t^{\frac{1}{2}}$$

Thus, we have −

$$a(t) = a_0 \left ( \frac{t}{t_0} \right )^{\frac{1}{2}}$$

From the above equation, we see that the rate of increase of scale factor is smaller than that of the dusty universe.

Points to Remember

  • Radiation prevalent in the present universe can be attributed very little to the stellar sources.

  • For a dusty universe, pressure is zero.

  • CMB is very cold.

Advertisements