Redshift and Recessional Velocity

Hubble’s observations made use of the fact that radial velocity is related to shifting of the Spectral Lines. Here, we will observe four cases and find a relationship between Recessional Velocity ($v_r$) and Red Shift (z).

Case 1: Non-Relativistic Case of Source moving

In this case, v is much less than c. Source is emitting some signal (sound, light, etc.), which is propagating as Wavefronts. The time interval between the sending of two consecutive signals in the source frame is Δts. The time interval between the reception of two consecutive signals in the observer frame is Δto.

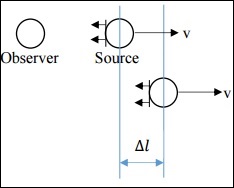
Source Moving

If both the observer and source are stationary, then Δts = Δto, but this is not the case here. Instead, the relation is as follows.

$$\Delta t_o = \Delta t_s + \frac{\Delta l}{c}$$

Now, $\Delta l = v \Delta t_s$

Also, since (wave speed x time) = wavelength, we get

$$\frac{\Delta t_o}{\Delta t_s} = \frac{\lambda_o}{\lambda_s}$$

From the above equations, we get the following relation −

$$\frac{\lambda_o}{\lambda_s} = 1 + \frac{v}{c}$$

where $\lambda _s$ is the wavelength of the signal at the source and $\lambda _o$ is the wavelength of the signal as interpreted by the observer.

Here, since the source is moving away from the observer, v is positive.

Red shift −

$$z = \frac{\lambda_o - \lambda_s}{\lambda_s} = \frac{\lambda_o}{\lambda_s} - 1$$

From the above equations, we get Red shift as follows.

$$z = \frac{v}{c}$$

Case 2: Non-Relativistic Case of Observer Moving

In this case, v is much less than c. Here, $\Delta l$ is different.

$$\Delta l = v \Delta t_o$$

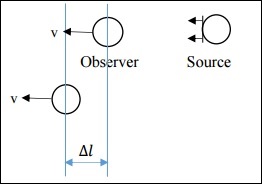
Non Relativistic

On simplification, we get −

$$\frac{\Delta t_o}{\Delta t_s} = \left ( 1 - \frac{v}{c} \right )^{-1}$$

We get Red shift as follows −

$$z = \frac{v/c}{1-v/c}$$

Since v << c, the red shift expression for both Case I and Case II are approximately the same.

Let us see how the red shifts obtained in the above two cases differ.

$$z_{II} - z_I = \frac{v}{c} \left [ \frac{1}{1 - v/c}-1 \right ]$$

Hence, $z_{II} − z_{I}$ is a very small number due to the $(v/c)^2$ factor.

This implies that, if v << c, we cannot tell whether the source is moving, or the observer is moving.

Let us now understand the Basics of STR (Special Theory of Relativity) −

  • Speed of light is a constant.

  • When the source (or observer) is moving with a speed comparable to the speed of light, relativistic effects are observed.

  • Time dilation: $\Delta t_o = \gamma \Delta t_s$

  • Length contraction: $\Delta l_o = \Delta t_s/\gamma$

  • Here, $\gamma$ is the Lorrentz factor, greater than 1.

$$\gamma = \frac{1}{\sqrt{1-(v^2/c^2)}}$$

Case 3: Relativistic Case of Source Moving

In this case, v is comparable to c. Refer to the same figure as in Case I. Due to the relativistic effect, time dilation is observed and hence the following relation is obtained. (Source is moving with relativistic speed)

$$\Delta t_o = \gamma \Delta t_s + \frac{\Delta l}{c}$$

$$\Delta l = \frac{v\gamma \Delta t_s}{c}$$

$$\frac{\Delta t_o}{\Delta t_s} = \frac{1 + v/c}{\sqrt{1- (v^2/c^2)}}$$

On further simplification, we get,

$$1 + z = \sqrt{\frac{1+v/c}{1-v/c}}$$

The above expression is known as the Kinematic Doppler Shift Expression.

Case 4: Relativistic Case of Observer Moving

Refer to the same figure as in Case II. Due to relativistic effect, time shortening is observed and hence the following relation is obtained. (Observer is moving with relativistic speed)

$$\Delta t_o = \frac{\Delta t_s}{\gamma}+\frac{\Delta l}{c}$$

$$\Delta l = \frac{v\Delta t_o}{c}$$

$$\frac{\Delta t_o}{\Delta t_s} = \frac{\sqrt{1-( v^2/c^2)}}{1-v/c}$$

On further simplification, we get −

$$1 + z = \sqrt{\frac{1+ v/c}{1- v/c}}$$

The above expression is the same as what we got for Case III.

Points to Remember

  • Recessional velocity and redshift of a star are related quantities.

  • In a non-relativistic case, we cannot determine whether the source is moving or stationary.

  • In a relativistic case, there is no difference in the redshift-recessional velocity relationship for source or observer moving.

  • Moving clocks move slower, is a direct result of relativity theory.

Advertisements