Cosmology - Matter Dominated Universe

---

---

In this chapter, we will discuss the Solutions to Friedmann Equations relating to the Matter Dominated Universe. In cosmology, because we are seeing everything in a large scale, the solar systems, galaxies, everything happens to be like dust particles (that’s what we see it with our eyes), we can call it dusty universe or matter only universe.

In the Fluid Equation,

$$\dot{\rho} = -3\left ( \frac{\dot{a}}{a} \right )\rho -3\left ( \frac{\dot{a}}{a} \right )\left ( \frac{P}{c^2} \right )$$

We can see there is a pressure term. For a dusty universe, P = 0, because the energy density of the matter will be greater than radiation pressure, and matter is not moving with relativistic speed.

So, the Fluid Equation will become,

$$\dot{\rho} = -3\left ( \frac{\dot{a}}{a} \right )\rho$$

$$\Rightarrow \dot{\rho}a + 3\dot{a}\rho = 0$$

$$\Rightarrow \frac{1}{a^3}\frac{\mathrm{d}}{\mathrm{d} t}(a^3 \rho) = 0$$

$$\Rightarrow \rho a^3 =\: constant$$

$$\Rightarrow \rho \propto \frac{1}{a^3}$$

There is no counter intuition in this equation because density should scale as $a^{-3}$ because Volume is increasing as $a^3$.

From the last relation, we can say that,

$$\frac{\rho (t)}{\rho_0} = \left [ \frac{a_0}{a(t)} \right ]^3$$

For the present universe, a, which is equal to a₀ should be 1. So,

$$\rho(t) = \frac{\rho_0}{a^3}$$

In a matter dominated flat universe, k = 0. So, Friedmann equation will become,

$$\left ( \frac{\dot{a}}{a} \right )^2 = \frac{8 \pi G\rho}{3}$$

$$\dot{a}^2 = \frac{8\pi G \rho a^2}{3}$$

By solving this equation, we will get,

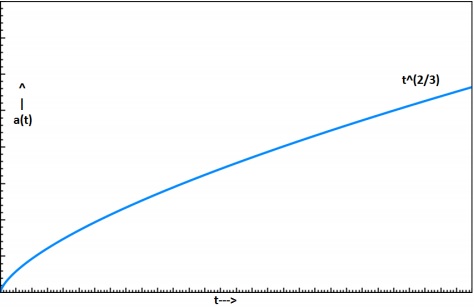
$$a \propto t^{2/3}$$

$$\frac{a(t)}{a_0} = \left ( \frac{t}{t_0} \right )^{2/3}$$

$$a(t) = \left( \frac{t}{t_0} \right )^{2/3}$$

This means that the universe will keep on increasing with a diminishing rate. The following image show the expansion of a Dusty Universe.

How ρ Changes with Time?

Take a look at the following equation −

$$\frac{\rho(t)}{\rho_0} = \left ( \frac{t_0}{t} \right )^2$$

We know that the scale factor changes with time as $t^{2/3}$. So,

$$a(t) = \left ( \frac{t}{t_0} \right )^{2/3}$$

Differentiating it, we will get,

$$\frac{(da)}{dt} = \dot{a} = \frac{2}{3} \left ( \frac{t^{-1/3}}{t_0} \right )$$

We know that the Hubble Constant is,

$$H(t) = \frac{\dot{a}}{a} = \frac{2}{3t}$$

This is the equation for Einstein-de sitter Universe. If we want to calculate the present age of the universe then,

$$t_0 = t_{age} = \frac{2}{3H_0}$$

After putting the value of $H_0$ for the present universe, we will get the value of the age of the universe as 9 Gyrs. There are many Globular Cluster in our own milky way galaxy which have ages more than that.

That was all about the dusty universe. Now, if you assume that the universe is dominated by radiation and not by matter, then the radiation energy density goes as $a^{-4}$ rather than $a^{-3}$. We will see more of it in the next chapter.

Points to Remember

• In cosmology, everything happens to be like dust particles, hence, we call it dusty universe or matter only universe.

• If we assume that the universe is dominated by radiation and not by matter, then the radiation energy density goes as $a^{-4}$ rather than $a^{-3}$.