Cosmology - Radial Velocity Method

In the previous chapter, the Radial Velocity Method for the case in which the orbital plane and the plane of sky are perpendicular was discussed for circular orbits. Here, we deal with one more case, when the orbital plane and the plane of sky are not perpendicular for circular orbits.

When the orbital plane is at an angle with respect to the plane of sky (not perpendicular), we have the following situation −

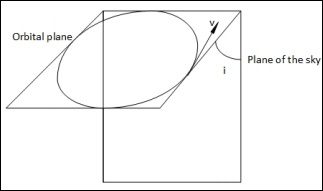
In this case, when they were perpendicular, we had two points at which we could measure the true velocity. But here, that is not possible. At all points, we can measure only a component of the true velocity, v.

$$v_r = v \:sin(i)cos(\theta)$$

where θ is the phase of the orbit which is a time-dependent quantity. The inclination angle i on the other hand, is time-independent. Hence,

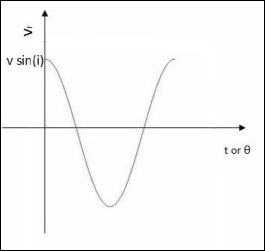
$$(v_r)_{max} = v\: sin(i)$$

The observed radial velocity curve will be of the following form −

When the orbital plane is perpendicular to the sky −

$$m_p = \left ( \frac{P}{2\pi G} \right )^{\frac{1}{3}}(M_\ast)^{\frac{2}{3}}v$$

where m_p, P, G, M∗ are mass of the planet, orbital period, universal gravitational constant and mass of the star respectively. But in this case, we should modify it as follows −

$$m_psin(i) = \left ( \frac{P}{2\pi G} \right )^{\frac{1}{3}} (M_\ast)^{\frac{2}{3}}(v_r)_{max}$$

But, finding the value of i is a difficult task. We can impose certain constraints on the value of i using transit method. The passage of the planet between the star and the Earth is called a transit. We can obtain the light curve by observing a transit and a significant dip in observed flux of a light curve implies that i is close to 90 degrees. If such conditions are not satisfied, we cannot have any idea on the value of i. Then the value of m_p that we find can serve as a lower limit for the mass of the planet, since it is actually m_p sin(i) and sin(i) ≤ 1.

To conclude, the Radial velocity method is more convenient than the transit method because radial velocity can be measured at any time but transit measurements can be made only during the transit which may not last for long.

Points to Remember

• Finding inclination of the planet’s orbit is not achieved by Radial Velocity method.

• Radial Velocity Method is better than the Transit Method because radial velocity can be measured always unlike transits.

• Transits are short-lived and very easy to miss.