
- Artificial Neural Network - Home
- Basic Concepts
- Building Blocks
- Learning & Adaptation
- Supervised Learning
- Unsupervised Learning
- Learning Vector Quantization
- Adaptive Resonance Theory
- Kohonen Self-Organizing Feature Maps
- Associate Memory Network
- Hopfield Networks
- Boltzmann Machine
- Brain-State-in-a-Box Network
- Optimization Using Hopfield Network
- Other Optimization Techniques
- Genetic Algorithm
- Applications of Neural Networks
Artificial Neural Network - Quick Guide
Artificial Neural Network - Basic Concepts
Neural networks are parallel computing devices, which is basically an attempt to make a computer model of the brain. The main objective is to develop a system to perform various computational tasks faster than the traditional systems. These tasks include pattern recognition and classification, approximation, optimization, and data clustering.
What is Artificial Neural Network?
Artificial Neural Network (ANN) is an efficient computing system whose central theme is borrowed from the analogy of biological neural networks. ANNs are also named as artificial neural systems, or parallel distributed processing systems, or connectionist systems. ANN acquires a large collection of units that are interconnected in some pattern to allow communication between the units. These units, also referred to as nodes or neurons, are simple processors which operate in parallel.
Every neuron is connected with other neuron through a connection link. Each connection link is associated with a weight that has information about the input signal. This is the most useful information for neurons to solve a particular problem because the weight usually excites or inhibits the signal that is being communicated. Each neuron has an internal state, which is called an activation signal. Output signals, which are produced after combining the input signals and activation rule, may be sent to other units.
A Brief History of ANN
The history of ANN can be divided into the following three eras −
ANN during 1940s to 1960s
Some key developments of this era are as follows −
1943 − It has been assumed that the concept of neural network started with the work of physiologist, Warren McCulloch, and mathematician, Walter Pitts, when in 1943 they modeled a simple neural network using electrical circuits in order to describe how neurons in the brain might work.
1949 − Donald Hebbs book, The Organization of Behavior, put forth the fact that repeated activation of one neuron by another increases its strength each time they are used.
1956 − An associative memory network was introduced by Taylor.
1958 − A learning method for McCulloch and Pitts neuron model named Perceptron was invented by Rosenblatt.
1960 − Bernard Widrow and Marcian Hoff developed models called "ADALINE" and MADALINE.
ANN during 1960s to 1980s
Some key developments of this era are as follows −
1961 − Rosenblatt made an unsuccessful attempt but proposed the backpropagation scheme for multilayer networks.
1964 − Taylor constructed a winner-take-all circuit with inhibitions among output units.
1969 − Multilayer perceptron (MLP) was invented by Minsky and Papert.
1971 − Kohonen developed Associative memories.
1976 − Stephen Grossberg and Gail Carpenter developed Adaptive resonance theory.
ANN from 1980s till Present
Some key developments of this era are as follows −
1982 − The major development was Hopfields Energy approach.
1985 − Boltzmann machine was developed by Ackley, Hinton, and Sejnowski.
1986 − Rumelhart, Hinton, and Williams introduced Generalised Delta Rule.
1988 − Kosko developed Binary Associative Memory (BAM) and also gave the concept of Fuzzy Logic in ANN.
The historical review shows that significant progress has been made in this field. Neural network based chips are emerging and applications to complex problems are being developed. Surely, today is a period of transition for neural network technology.
Biological Neuron
A nerve cell (neuron) is a special biological cell that processes information. According to an estimation, there are huge number of neurons, approximately 1011 with numerous interconnections, approximately 1015.
Schematic Diagram
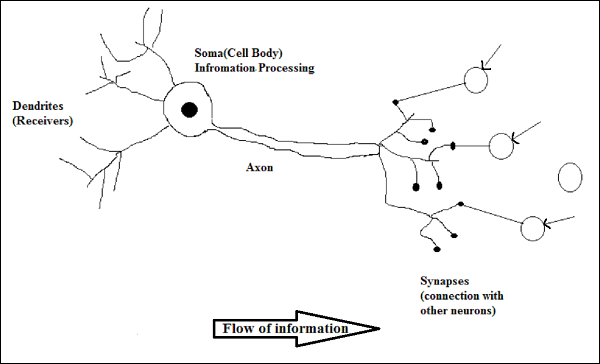
Working of a Biological Neuron
As shown in the above diagram, a typical neuron consists of the following four parts with the help of which we can explain its working −
Dendrites − They are tree-like branches, responsible for receiving the information from other neurons it is connected to. In other sense, we can say that they are like the ears of neuron.
Soma − It is the cell body of the neuron and is responsible for processing of information, they have received from dendrites.
Axon − It is just like a cable through which neurons send the information.
Synapses − It is the connection between the axon and other neuron dendrites.
ANN versus BNN
Before taking a look at the differences between Artificial Neural Network (ANN) and Biological Neural Network (BNN), let us take a look at the similarities based on the terminology between these two.
| Biological Neural Network (BNN) | Artificial Neural Network (ANN) |
|---|---|
| Soma | Node |
| Dendrites | Input |
| Synapse | Weights or Interconnections |
| Axon | Output |
The following table shows the comparison between ANN and BNN based on some criteria mentioned.
| Criteria | BNN | ANN |
|---|---|---|
| Processing | Massively parallel, slow but superior than ANN | Massively parallel, fast but inferior than BNN |
| Size | 1011 neurons and 1015 interconnections | 102 to 104 nodes (mainly depends on the type of application and network designer) |
| Learning | They can tolerate ambiguity | Very precise, structured and formatted data is required to tolerate ambiguity |
| Fault tolerance | Performance degrades with even partial damage | It is capable of robust performance, hence has the potential to be fault tolerant |
| Storage capacity | Stores the information in the synapse | Stores the information in continuous memory locations |
Model of Artificial Neural Network
The following diagram represents the general model of ANN followed by its processing.
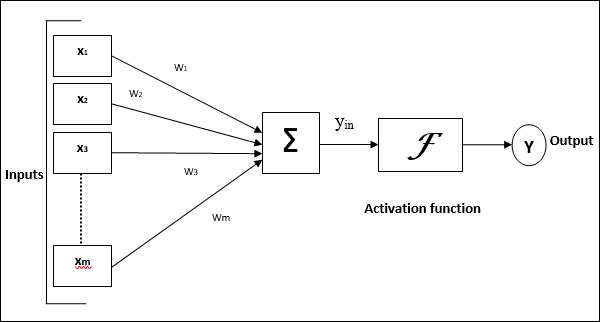
For the above general model of artificial neural network, the net input can be calculated as follows −
$$y_{in}\:=\:x_{1}.w_{1}\:+\:x_{2}.w_{2}\:+\:x_{3}.w_{3}\:\dotso\: x_{m}.w_{m}$$
i.e., Net input $y_{in}\:=\:\sum_i^m\:x_{i}.w_{i}$
The output can be calculated by applying the activation function over the net input.
$$Y\:=\:F(y_{in}) $$
Output = function (net input calculated)
Artificial Neural Network - Building Blocks
Processing of ANN depends upon the following three building blocks −
- Network Topology
- Adjustments of Weights or Learning
- Activation Functions
In this chapter, we will discuss in detail about these three building blocks of ANN
Network Topology
A network topology is the arrangement of a network along with its nodes and connecting lines. According to the topology, ANN can be classified as the following kinds −
Feedforward Network
It is a non-recurrent network having processing units/nodes in layers and all the nodes in a layer are connected with the nodes of the previous layers. The connection has different weights upon them. There is no feedback loop means the signal can only flow in one direction, from input to output. It may be divided into the following two types −
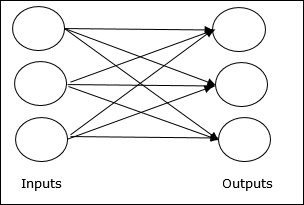
Single layer feedforward network − The concept is of feedforward ANN having only one weighted layer. In other words, we can say the input layer is fully connected to the output layer.
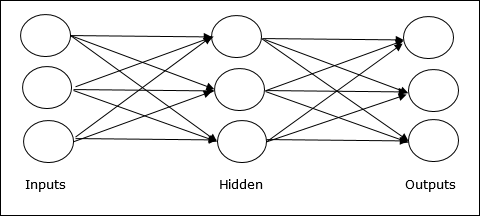
Multilayer feedforward network − The concept is of feedforward ANN having more than one weighted layer. As this network has one or more layers between the input and the output layer, it is called hidden layers.
Feedback Network
As the name suggests, a feedback network has feedback paths, which means the signal can flow in both directions using loops. This makes it a non-linear dynamic system, which changes continuously until it reaches a state of equilibrium. It may be divided into the following types −
Recurrent networks − They are feedback networks with closed loops. Following are the two types of recurrent networks.
Fully recurrent network − It is the simplest neural network architecture because all nodes are connected to all other nodes and each node works as both input and output.
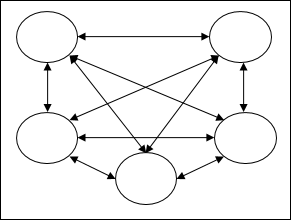
Jordan network − It is a closed loop network in which the output will go to the input again as feedback as shown in the following diagram.
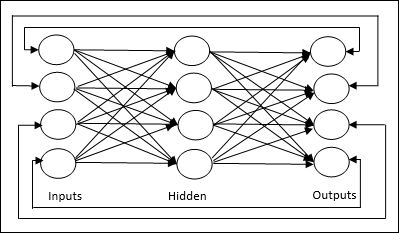
Adjustments of Weights or Learning
Learning, in artificial neural network, is the method of modifying the weights of connections between the neurons of a specified network. Learning in ANN can be classified into three categories namely supervised learning, unsupervised learning, and reinforcement learning.
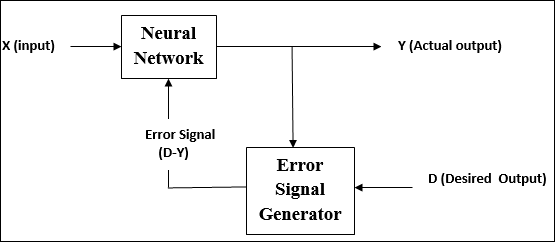
Supervised Learning
As the name suggests, this type of learning is done under the supervision of a teacher. This learning process is dependent.
During the training of ANN under supervised learning, the input vector is presented to the network, which will give an output vector. This output vector is compared with the desired output vector. An error signal is generated, if there is a difference between the actual output and the desired output vector. On the basis of this error signal, the weights are adjusted until the actual output is matched with the desired output.
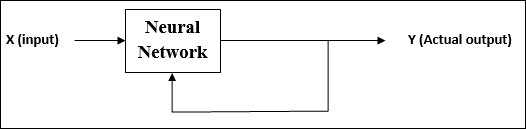
Unsupervised Learning
As the name suggests, this type of learning is done without the supervision of a teacher. This learning process is independent.
During the training of ANN under unsupervised learning, the input vectors of similar type are combined to form clusters. When a new input pattern is applied, then the neural network gives an output response indicating the class to which the input pattern belongs.
There is no feedback from the environment as to what should be the desired output and if it is correct or incorrect. Hence, in this type of learning, the network itself must discover the patterns and features from the input data, and the relation for the input data over the output.
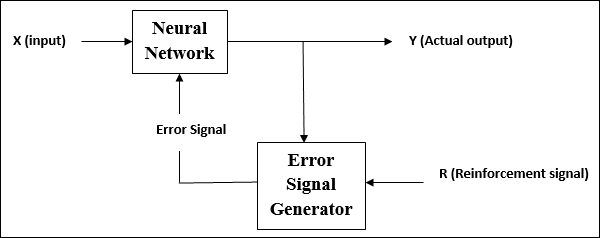
Reinforcement Learning
As the name suggests, this type of learning is used to reinforce or strengthen the network over some critic information. This learning process is similar to supervised learning, however we might have very less information.
During the training of network under reinforcement learning, the network receives some feedback from the environment. This makes it somewhat similar to supervised learning. However, the feedback obtained here is evaluative not instructive, which means there is no teacher as in supervised learning. After receiving the feedback, the network performs adjustments of the weights to get better critic information in future.
Activation Functions
It may be defined as the extra force or effort applied over the input to obtain an exact output. In ANN, we can also apply activation functions over the input to get the exact output. Followings are some activation functions of interest −
Linear Activation Function
It is also called the identity function as it performs no input editing. It can be defined as −
$$F(x)\:=\:x$$
Sigmoid Activation Function
It is of two type as follows −
Binary sigmoidal function − This activation function performs input editing between 0 and 1. It is positive in nature. It is always bounded, which means its output cannot be less than 0 and more than 1. It is also strictly increasing in nature, which means more the input higher would be the output. It can be defined as
$$F(x)\:=\:sigm(x)\:=\:\frac{1}{1\:+\:exp(-x)}$$
Bipolar sigmoidal function − This activation function performs input editing between -1 and 1. It can be positive or negative in nature. It is always bounded, which means its output cannot be less than -1 and more than 1. It is also strictly increasing in nature like sigmoid function. It can be defined as
$$F(x)\:=\:sigm(x)\:=\:\frac{2}{1\:+\:exp(-x)}\:-\:1\:=\:\frac{1\:-\:exp(x)}{1\:+\:exp(x)}$$
Learning and Adaptation
As stated earlier, ANN is completely inspired by the way biological nervous system, i.e. the human brain works. The most impressive characteristic of the human brain is to learn, hence the same feature is acquired by ANN.
What Is Learning in ANN?
Basically, learning means to do and adapt the change in itself as and when there is a change in environment. ANN is a complex system or more precisely we can say that it is a complex adaptive system, which can change its internal structure based on the information passing through it.
Why Is It important?
Being a complex adaptive system, learning in ANN implies that a processing unit is capable of changing its input/output behavior due to the change in environment. The importance of learning in ANN increases because of the fixed activation function as well as the input/output vector, when a particular network is constructed. Now to change the input/output behavior, we need to adjust the weights.
Classification
It may be defined as the process of learning to distinguish the data of samples into different classes by finding common features between the samples of the same classes. For example, to perform training of ANN, we have some training samples with unique features, and to perform its testing we have some testing samples with other unique features. Classification is an example of supervised learning.
Neural Network Learning Rules
We know that, during ANN learning, to change the input/output behavior, we need to adjust the weights. Hence, a method is required with the help of which the weights can be modified. These methods are called Learning rules, which are simply algorithms or equations. Following are some learning rules for the neural network −
Hebbian Learning Rule
This rule, one of the oldest and simplest, was introduced by Donald Hebb in his book The Organization of Behavior in 1949. It is a kind of feed-forward, unsupervised learning.
Basic Concept − This rule is based on a proposal given by Hebb, who wrote −
When an axon of cell A is near enough to excite a cell B and repeatedly or persistently takes part in firing it, some growth process or metabolic change takes place in one or both cells such that As efficiency, as one of the cells firing B, is increased.
From the above postulate, we can conclude that the connections between two neurons might be strengthened if the neurons fire at the same time and might weaken if they fire at different times.
Mathematical Formulation − According to Hebbian learning rule, following is the formula to increase the weight of connection at every time step.
$$\Delta w_{ji}(t)\:=\:\alpha x_{i}(t).y_{j}(t)$$
Here, $\Delta w_{ji}(t)$ = increment by which the weight of connection increases at time step t
$\alpha$ = the positive and constant learning rate
$x_{i}(t)$ = the input value from pre-synaptic neuron at time step t
$y_{i}(t)$ = the output of pre-synaptic neuron at same time step t
Perceptron Learning Rule
This rule is an error correcting the supervised learning algorithm of single layer feedforward networks with linear activation function, introduced by Rosenblatt.
Basic Concept − As being supervised in nature, to calculate the error, there would be a comparison between the desired/target output and the actual output. If there is any difference found, then a change must be made to the weights of connection.
Mathematical Formulation − To explain its mathematical formulation, suppose we have n number of finite input vectors, x(n), along with its desired/target output vector t(n), where n = 1 to N.
Now the output y can be calculated, as explained earlier on the basis of the net input, and activation function being applied over that net input can be expressed as follows −
$$y\:=\:f(y_{in})\:=\:\begin{cases}1, & y_{in}\:>\:\theta \\0, & y_{in}\:\leqslant\:\theta\end{cases}$$
Where θ is threshold.
The updating of weight can be done in the following two cases −
Case I − when t ≠ y, then
$$w(new)\:=\:w(old)\:+\;tx$$
Case II − when t = y, then
No change in weight
Delta Learning Rule (Widrow-Hoff Rule)
It is introduced by Bernard Widrow and Marcian Hoff, also called Least Mean Square (LMS) method, to minimize the error over all training patterns. It is kind of supervised learning algorithm with having continuous activation function.
Basic Concept − The base of this rule is gradient-descent approach, which continues forever. Delta rule updates the synaptic weights so as to minimize the net input to the output unit and the target value.
Mathematical Formulation − To update the synaptic weights, delta rule is given by
$$\Delta w_{i}\:=\:\alpha\:.x_{i}.e_{j}$$
Here $\Delta w_{i}$ = weight change for ith pattern;
$\alpha$ = the positive and constant learning rate;
$x_{i}$ = the input value from pre-synaptic neuron;
$e_{j}$ = $(t\:-\:y_{in})$, the difference between the desired/target output and the actual output $y_{in}$
The above delta rule is for a single output unit only.
The updating of weight can be done in the following two cases −
Case-I − when t ≠ y, then
$$w(new)\:=\:w(old)\:+\:\Delta w$$
Case-II − when t = y, then
No change in weight
Competitive Learning Rule (Winner-takes-all)
It is concerned with unsupervised training in which the output nodes try to compete with each other to represent the input pattern. To understand this learning rule, we must understand the competitive network which is given as follows −
Basic Concept of Competitive Network − This network is just like a single layer feedforward network with feedback connection between outputs. The connections between outputs are inhibitory type, shown by dotted lines, which means the competitors never support themselves.
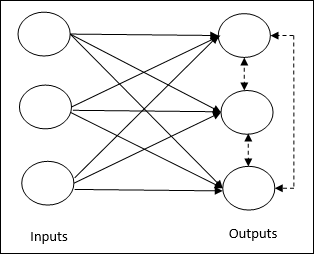
Basic Concept of Competitive Learning Rule − As said earlier, there will be a competition among the output nodes. Hence, the main concept is that during training, the output unit with the highest activation to a given input pattern, will be declared the winner. This rule is also called Winner-takes-all because only the winning neuron is updated and the rest of the neurons are left unchanged.
Mathematical formulation − Following are the three important factors for mathematical formulation of this learning rule −
Condition to be a winner − Suppose if a neuron $y_{k}$ wants to be the winner then there would be the following condition −
$$y_{k}\:=\:\begin{cases}1 & if\:v_{k}\:>\:v_{j}\:for\:all\:j,\:j\:\neq\:k\\0 & otherwise\end{cases}$$
It means that if any neuron, say $y_{k}$ , wants to win, then its induced local field (the output of summation unit), say $v_{k}$, must be the largest among all the other neurons in the network.
Condition of sum total of weight − Another constraint over the competitive learning rule is, the sum total of weights to a particular output neuron is going to be 1. For example, if we consider neuron k then −
$$\displaystyle\sum\limits_{j}w_{kj}\:=\:1\:\:\:\:\:\:\:\:\:for\:all\:k$$
Change of weight for winner − If a neuron does not respond to the input pattern, then no learning takes place in that neuron. However, if a particular neuron wins, then the corresponding weights are adjusted as follows
$$\Delta w_{kj}\:=\:\begin{cases}-\alpha(x_{j}\:-\:w_{kj}), & if\:neuron\:k\:wins\\0, & if\:neuron\:k\:losses\end{cases}$$
Here $\alpha$ is the learning rate.
This clearly shows that we are favoring the winning neuron by adjusting its weight and if there is a neuron loss, then we need not bother to re-adjust its weight.
Outstar Learning Rule
This rule, introduced by Grossberg, is concerned with supervised learning because the desired outputs are known. It is also called Grossberg learning.
Basic Concept − This rule is applied over the neurons arranged in a layer. It is specially designed to produce a desired output d of the layer of p neurons.
Mathematical Formulation − The weight adjustments in this rule are computed as follows
$$\Delta w_{j}\:=\:\alpha\:(d\:-\:w_{j})$$
Here d is the desired neuron output and $\alpha$ is the learning rate.
Supervised Learning
As the name suggests, supervised learning takes place under the supervision of a teacher. This learning process is dependent. During the training of ANN under supervised learning, the input vector is presented to the network, which will produce an output vector. This output vector is compared with the desired/target output vector. An error signal is generated if there is a difference between the actual output and the desired/target output vector. On the basis of this error signal, the weights would be adjusted until the actual output is matched with the desired output.
Perceptron
Developed by Frank Rosenblatt by using McCulloch and Pitts model, perceptron is the basic operational unit of artificial neural networks. It employs supervised learning rule and is able to classify the data into two classes.
Operational characteristics of the perceptron: It consists of a single neuron with an arbitrary number of inputs along with adjustable weights, but the output of the neuron is 1 or 0 depending upon the threshold. It also consists of a bias whose weight is always 1. Following figure gives a schematic representation of the perceptron.
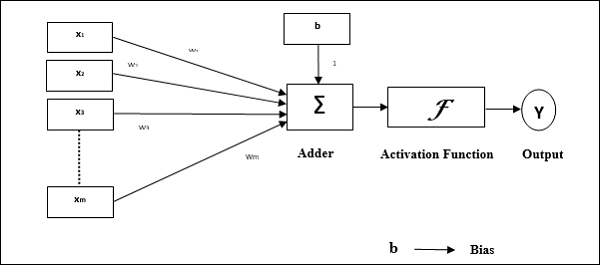
Perceptron thus has the following three basic elements −
Links − It would have a set of connection links, which carries a weight including a bias always having weight 1.
Adder − It adds the input after they are multiplied with their respective weights.
Activation function − It limits the output of neuron. The most basic activation function is a Heaviside step function that has two possible outputs. This function returns 1, if the input is positive, and 0 for any negative input.
Training Algorithm
Perceptron network can be trained for single output unit as well as multiple output units.
Training Algorithm for Single Output Unit
Step 1 − Initialize the following to start the training −
- Weights
- Bias
- Learning rate $\alpha$
For easy calculation and simplicity, weights and bias must be set equal to 0 and the learning rate must be set equal to 1.
Step 2 − Continue step 3-8 when the stopping condition is not true.
Step 3 − Continue step 4-6 for every training vector x.
Step 4 − Activate each input unit as follows −
$$x_{i}\:=\:s_{i}\:(i\:=\:1\:to\:n)$$
Step 5 − Now obtain the net input with the following relation −
$$y_{in}\:=\:b\:+\:\displaystyle\sum\limits_{i}^n x_{i}.\:w_{i}$$
Here b is bias and n is the total number of input neurons.
Step 6 − Apply the following activation function to obtain the final output.
$$f(y_{in})\:=\:\begin{cases}1 & if\:y_{in}\:>\:\theta\\0 & if \: -\theta\:\leqslant\:y_{in}\:\leqslant\:\theta\\-1 & if\:y_{in}\:
Step 7 − Adjust the weight and bias as follows −
Case 1 − if y ≠ t then,
$$w_{i}(new)\:=\:w_{i}(old)\:+\:\alpha\:tx_{i}$$
$$b(new)\:=\:b(old)\:+\:\alpha t$$
Case 2 − if y = t then,
$$w_{i}(new)\:=\:w_{i}(old)$$
$$b(new)\:=\:b(old)$$
Here y is the actual output and t is the desired/target output.
Step 8 − Test for the stopping condition, which would happen when there is no change in weight.
Training Algorithm for Multiple Output Units
The following diagram is the architecture of perceptron for multiple output classes.
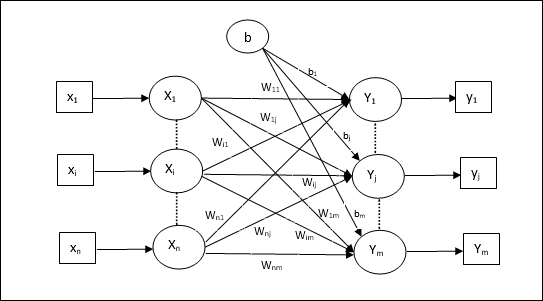
Step 1 − Initialize the following to start the training −
- Weights
- Bias
- Learning rate $\alpha$
For easy calculation and simplicity, weights and bias must be set equal to 0 and the learning rate must be set equal to 1.
Step 2 − Continue step 3-8 when the stopping condition is not true.
Step 3 − Continue step 4-6 for every training vector x.
Step 4 − Activate each input unit as follows −
$$x_{i}\:=\:s_{i}\:(i\:=\:1\:to\:n)$$
Step 5 − Obtain the net input with the following relation −
$$y_{in}\:=\:b\:+\:\displaystyle\sum\limits_{i}^n x_{i}\:w_{ij}$$
Here b is bias and n is the total number of input neurons.
Step 6 − Apply the following activation function to obtain the final output for each output unit j = 1 to m −
$$f(y_{in})\:=\:\begin{cases}1 & if\:y_{inj}\:>\:\theta\\0 & if \: -\theta\:\leqslant\:y_{inj}\:\leqslant\:\theta\\-1 & if\:y_{inj}\:
Step 7 − Adjust the weight and bias for x = 1 to n and j = 1 to m as follows −
Case 1 − if yj ≠ tj then,
$$w_{ij}(new)\:=\:w_{ij}(old)\:+\:\alpha\:t_{j}x_{i}$$
$$b_{j}(new)\:=\:b_{j}(old)\:+\:\alpha t_{j}$$
Case 2 − if yj = tj then,
$$w_{ij}(new)\:=\:w_{ij}(old)$$
$$b_{j}(new)\:=\:b_{j}(old)$$
Here y is the actual output and t is the desired/target output.
Step 8 − Test for the stopping condition, which will happen when there is no change in weight.
Adaptive Linear Neuron (Adaline)
Adaline which stands for Adaptive Linear Neuron, is a network having a single linear unit. It was developed by Widrow and Hoff in 1960. Some important points about Adaline are as follows −
It uses bipolar activation function.
It uses delta rule for training to minimize the Mean-Squared Error (MSE) between the actual output and the desired/target output.
The weights and the bias are adjustable.
Architecture
The basic structure of Adaline is similar to perceptron having an extra feedback loop with the help of which the actual output is compared with the desired/target output. After comparison on the basis of training algorithm, the weights and bias will be updated.
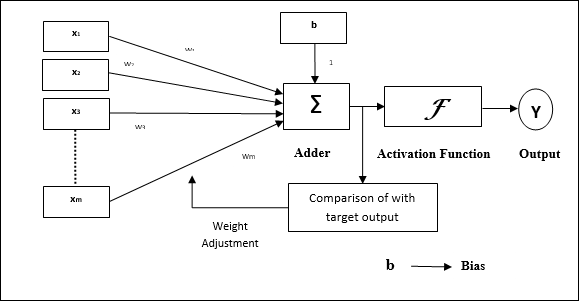
Training Algorithm
Step 1 − Initialize the following to start the training −
- Weights
- Bias
- Learning rate $\alpha$
For easy calculation and simplicity, weights and bias must be set equal to 0 and the learning rate must be set equal to 1.
Step 2 − Continue step 3-8 when the stopping condition is not true.
Step 3 − Continue step 4-6 for every bipolar training pair s:t.
Step 4 − Activate each input unit as follows −
$$x_{i}\:=\:s_{i}\:(i\:=\:1\:to\:n)$$
Step 5 − Obtain the net input with the following relation −
$$y_{in}\:=\:b\:+\:\displaystyle\sum\limits_{i}^n x_{i}\:w_{i}$$
Here b is bias and n is the total number of input neurons.
Step 6 − Apply the following activation function to obtain the final output −
$$f(y_{in})\:=\:\begin{cases}1 & if\:y_{in}\:\geqslant\:0 \\-1 & if\:y_{in}\:
Step 7 − Adjust the weight and bias as follows −
Case 1 − if y ≠ t then,
$$w_{i}(new)\:=\:w_{i}(old)\:+\: \alpha(t\:-\:y_{in})x_{i}$$
$$b(new)\:=\:b(old)\:+\: \alpha(t\:-\:y_{in})$$
Case 2 − if y = t then,
$$w_{i}(new)\:=\:w_{i}(old)$$
$$b(new)\:=\:b(old)$$
Here y is the actual output and t is the desired/target output.
$(t\:-\;y_{in})$ is the computed error.
Step 8 − Test for the stopping condition, which will happen when there is no change in weight or the highest weight change occurred during training is smaller than the specified tolerance.
Multiple Adaptive Linear Neuron (Madaline)
Madaline which stands for Multiple Adaptive Linear Neuron, is a network which consists of many Adalines in parallel. It will have a single output unit. Some important points about Madaline are as follows −
It is just like a multilayer perceptron, where Adaline will act as a hidden unit between the input and the Madaline layer.
The weights and the bias between the input and Adaline layers, as in we see in the Adaline architecture, are adjustable.
The Adaline and Madaline layers have fixed weights and bias of 1.
Training can be done with the help of Delta rule.
Architecture
The architecture of Madaline consists of n neurons of the input layer, m neurons of the Adaline layer, and 1 neuron of the Madaline layer. The Adaline layer can be considered as the hidden layer as it is between the input layer and the output layer, i.e. the Madaline layer.
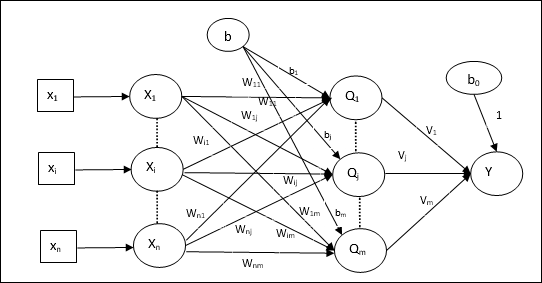
Training Algorithm
By now we know that only the weights and bias between the input and the Adaline layer are to be adjusted, and the weights and bias between the Adaline and the Madaline layer are fixed.
Step 1 − Initialize the following to start the training −
- Weights
- Bias
- Learning rate $\alpha$
For easy calculation and simplicity, weights and bias must be set equal to 0 and the learning rate must be set equal to 1.
Step 2 − Continue step 3-8 when the stopping condition is not true.
Step 3 − Continue step 4-7 for every bipolar training pair s:t.
Step 4 − Activate each input unit as follows −
$$x_{i}\:=\:s_{i}\:(i\:=\:1\:to\:n)$$
Step 5 − Obtain the net input at each hidden layer, i.e. the Adaline layer with the following relation −
$$Q_{inj}\:=\:b_{j}\:+\:\displaystyle\sum\limits_{i}^n x_{i}\:w_{ij}\:\:\:j\:=\:1\:to\:m$$
Here b is bias and n is the total number of input neurons.
Step 6 − Apply the following activation function to obtain the final output at the Adaline and the Madaline layer −
$$f(x)\:=\:\begin{cases}1 & if\:x\:\geqslant\:0 \\-1 & if\:x\:
Output at the hidden (Adaline) unit
$$Q_{j}\:=\:f(Q_{inj})$$
Final output of the network
$$y\:=\:f(y_{in})$$
i.e. $\:\:y_{inj}\:=\:b_{0}\:+\:\sum_{j = 1}^m\:Q_{j}\:v_{j}$
Step 7 − Calculate the error and adjust the weights as follows −
Case 1 − if y ≠ t and t = 1 then,
$$w_{ij}(new)\:=\:w_{ij}(old)\:+\: \alpha(1\:-\:Q_{inj})x_{i}$$
$$b_{j}(new)\:=\:b_{j}(old)\:+\: \alpha(1\:-\:Q_{inj})$$
In this case, the weights would be updated on Qj where the net input is close to 0 because t = 1.
Case 2 − if y ≠ t and t = -1 then,
$$w_{ik}(new)\:=\:w_{ik}(old)\:+\: \alpha(-1\:-\:Q_{ink})x_{i}$$
$$b_{k}(new)\:=\:b_{k}(old)\:+\: \alpha(-1\:-\:Q_{ink})$$
In this case, the weights would be updated on Qk where the net input is positive because t = -1.
Here y is the actual output and t is the desired/target output.
Case 3 − if y = t then
There would be no change in weights.
Step 8 − Test for the stopping condition, which will happen when there is no change in weight or the highest weight change occurred during training is smaller than the specified tolerance.
Back Propagation Neural Networks
Back Propagation Neural (BPN) is a multilayer neural network consisting of the input layer, at least one hidden layer and output layer. As its name suggests, back propagating will take place in this network. The error which is calculated at the output layer, by comparing the target output and the actual output, will be propagated back towards the input layer.
Architecture
As shown in the diagram, the architecture of BPN has three interconnected layers having weights on them. The hidden layer as well as the output layer also has bias, whose weight is always 1, on them. As is clear from the diagram, the working of BPN is in two phases. One phase sends the signal from the input layer to the output layer, and the other phase back propagates the error from the output layer to the input layer.
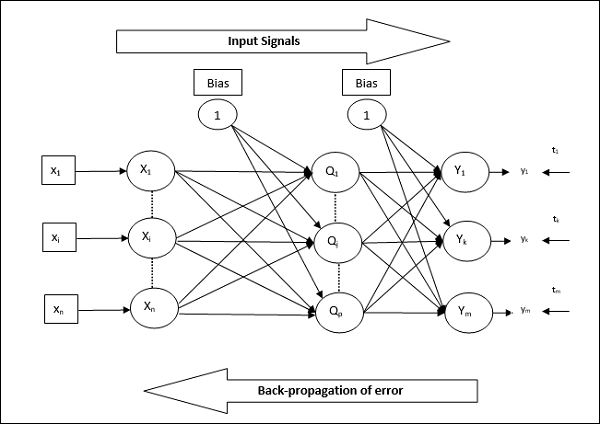
Training Algorithm
For training, BPN will use binary sigmoid activation function. The training of BPN will have the following three phases.
Phase 1 − Feed Forward Phase
Phase 2 − Back Propagation of error
Phase 3 − Updating of weights
All these steps will be concluded in the algorithm as follows
Step 1 − Initialize the following to start the training −
- Weights
- Learning rate $\alpha$
For easy calculation and simplicity, take some small random values.
Step 2 − Continue step 3-11 when the stopping condition is not true.
Step 3 − Continue step 4-10 for every training pair.
Phase 1
Step 4 − Each input unit receives input signal xi and sends it to the hidden unit for all i = 1 to n
Step 5 − Calculate the net input at the hidden unit using the following relation −
$$Q_{inj}\:=\:b_{0j}\:+\:\sum_{i=1}^n x_{i}v_{ij}\:\:\:\:j\:=\:1\:to\:p$$
Here b0j is the bias on hidden unit, vij is the weight on j unit of the hidden layer coming from i unit of the input layer.
Now calculate the net output by applying the following activation function
$$Q_{j}\:=\:f(Q_{inj})$$
Send these output signals of the hidden layer units to the output layer units.
Step 6 − Calculate the net input at the output layer unit using the following relation −
$$y_{ink}\:=\:b_{0k}\:+\:\sum_{j = 1}^p\:Q_{j}\:w_{jk}\:\:k\:=\:1\:to\:m$$
Here b0k is the bias on output unit, wjk is the weight on k unit of the output layer coming from j unit of the hidden layer.
Calculate the net output by applying the following activation function
$$y_{k}\:=\:f(y_{ink})$$
Phase 2
Step 7 − Compute the error correcting term, in correspondence with the target pattern received at each output unit, as follows −
$$\delta_{k}\:=\:(t_{k}\:-\:y_{k})f^{'}(y_{ink})$$
On this basis, update the weight and bias as follows −
$$\Delta v_{jk}\:=\:\alpha \delta_{k}\:Q_{ij}$$
$$\Delta b_{0k}\:=\:\alpha \delta_{k}$$
Then, send $\delta_{k}$ back to the hidden layer.
Step 8 − Now each hidden unit will be the sum of its delta inputs from the output units.
$$\delta_{inj}\:=\:\displaystyle\sum\limits_{k=1}^m \delta_{k}\:w_{jk}$$
Error term can be calculated as follows −
$$\delta_{j}\:=\:\delta_{inj}f^{'}(Q_{inj})$$
On this basis, update the weight and bias as follows −
$$\Delta w_{ij}\:=\:\alpha\delta_{j}x_{i}$$
$$\Delta b_{0j}\:=\:\alpha\delta_{j}$$
Phase 3
Step 9 − Each output unit (ykk = 1 to m) updates the weight and bias as follows −
$$v_{jk}(new)\:=\:v_{jk}(old)\:+\:\Delta v_{jk}$$
$$b_{0k}(new)\:=\:b_{0k}(old)\:+\:\Delta b_{0k}$$
Step 10 − Each output unit (zjj = 1 to p) updates the weight and bias as follows −
$$w_{ij}(new)\:=\:w_{ij}(old)\:+\:\Delta w_{ij}$$
$$b_{0j}(new)\:=\:b_{0j}(old)\:+\:\Delta b_{0j}$$
Step 11 − Check for the stopping condition, which may be either the number of epochs reached or the target output matches the actual output.
Generalized Delta Learning Rule
Delta rule works only for the output layer. On the other hand, generalized delta rule, also called as back-propagation rule, is a way of creating the desired values of the hidden layer.
Mathematical Formulation
For the activation function $y_{k}\:=\:f(y_{ink})$ the derivation of net input on Hidden layer as well as on output layer can be given by
$$y_{ink}\:=\:\displaystyle\sum\limits_i\:z_{i}w_{jk}$$
And $\:\:y_{inj}\:=\:\sum_i x_{i}v_{ij}$
Now the error which has to be minimized is
$$E\:=\:\frac{1}{2}\displaystyle\sum\limits_{k}\:[t_{k}\:-\:y_{k}]^2$$
By using the chain rule, we have
$$\frac{\partial E}{\partial w_{jk}}\:=\:\frac{\partial }{\partial w_{jk}}(\frac{1}{2}\displaystyle\sum\limits_{k}\:[t_{k}\:-\:y_{k}]^2)$$
$$=\:\frac{\partial }{\partial w_{jk}}\lgroup\frac{1}{2}[t_{k}\:-\:t(y_{ink})]^2\rgroup$$
$$=\:-[t_{k}\:-\:y_{k}]\frac{\partial }{\partial w_{jk}}f(y_{ink})$$
$$=\:-[t_{k}\:-\:y_{k}]f(y_{ink})\frac{\partial }{\partial w_{jk}}(y_{ink})$$
$$=\:-[t_{k}\:-\:y_{k}]f^{'}(y_{ink})z_{j}$$
Now let us say $\delta_{k}\:=\:-[t_{k}\:-\:y_{k}]f^{'}(y_{ink})$
The weights on connections to the hidden unit zj can be given by −
$$\frac{\partial E}{\partial v_{ij}}\:=\:- \displaystyle\sum\limits_{k} \delta_{k}\frac{\partial }{\partial v_{ij}}\:(y_{ink})$$
Putting the value of $y_{ink}$ we will get the following
$$\delta_{j}\:=\:-\displaystyle\sum\limits_{k}\delta_{k}w_{jk}f^{'}(z_{inj})$$
Weight updating can be done as follows −
For the output unit −
$$\Delta w_{jk}\:=\:-\alpha\frac{\partial E}{\partial w_{jk}}$$
$$=\:\alpha\:\delta_{k}\:z_{j}$$
For the hidden unit −
$$\Delta v_{ij}\:=\:-\alpha\frac{\partial E}{\partial v_{ij}}$$
$$=\:\alpha\:\delta_{j}\:x_{i}$$
Unsupervised Learning
As the name suggests, this type of learning is done without the supervision of a teacher. This learning process is independent. During the training of ANN under unsupervised learning, the input vectors of similar type are combined to form clusters. When a new input pattern is applied, then the neural network gives an output response indicating the class to which input pattern belongs. In this, there would be no feedback from the environment as to what should be the desired output and whether it is correct or incorrect. Hence, in this type of learning the network itself must discover the patterns, features from the input data and the relation for the input data over the output.
Winner-Takes-All Networks
These kinds of networks are based on the competitive learning rule and will use the strategy where it chooses the neuron with the greatest total inputs as a winner. The connections between the output neurons show the competition between them and one of them would be ON which means it would be the winner and others would be OFF.
Following are some of the networks based on this simple concept using unsupervised learning.
Hamming Network
In most of the neural networks using unsupervised learning, it is essential to compute the distance and perform comparisons. This kind of network is Hamming network, where for every given input vectors, it would be clustered into different groups. Following are some important features of Hamming Networks −
Lippmann started working on Hamming networks in 1987.
It is a single layer network.
The inputs can be either binary {0, 1} of bipolar {-1, 1}.
The weights of the net are calculated by the exemplar vectors.
It is a fixed weight network which means the weights would remain the same even during training.
Max Net
This is also a fixed weight network, which serves as a subnet for selecting the node having the highest input. All the nodes are fully interconnected and there exists symmetrical weights in all these weighted interconnections.
Architecture
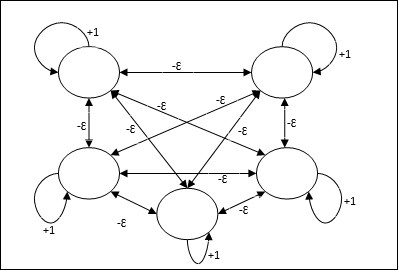
It uses the mechanism which is an iterative process and each node receives inhibitory inputs from all other nodes through connections. The single node whose value is maximum would be active or winner and the activations of all other nodes would be inactive. Max Net uses identity activation function with $$f(x)\:=\:\begin{cases}x & if\:x > 0\\0 & if\:x \leq 0\end{cases}$$
The task of this net is accomplished by the self-excitation weight of +1 and mutual inhibition magnitude, which is set like [0 < ɛ < $\frac{1}{m}$] where m is the total number of the nodes.
Competitive Learning in ANN
It is concerned with unsupervised training in which the output nodes try to compete with each other to represent the input pattern. To understand this learning rule we will have to understand competitive net which is explained as follows −
Basic Concept of Competitive Network
This network is just like a single layer feed-forward network having feedback connection between the outputs. The connections between the outputs are inhibitory type, which is shown by dotted lines, which means the competitors never support themselves.
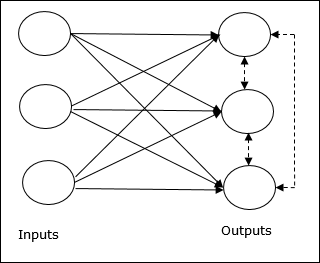
Basic Concept of Competitive Learning Rule
As said earlier, there would be competition among the output nodes so the main concept is - during training, the output unit that has the highest activation to a given input pattern, will be declared the winner. This rule is also called Winner-takes-all because only the winning neuron is updated and the rest of the neurons are left unchanged.
Mathematical Formulation
Following are the three important factors for mathematical formulation of this learning rule −
Condition to be a winner
Suppose if a neuron yk wants to be the winner, then there would be the following condition
$$y_{k}\:=\:\begin{cases}1 & if\:v_{k} > v_{j}\:for\:all\:\:j,\:j\:\neq\:k\\0 & otherwise\end{cases}$$
It means that if any neuron, say, yk wants to win, then its induced local field (the output of the summation unit), say vk, must be the largest among all the other neurons in the network.
Condition of the sum total of weight
Another constraint over the competitive learning rule is the sum total of weights to a particular output neuron is going to be 1. For example, if we consider neuron k then
$$\displaystyle\sum\limits_{k} w_{kj}\:=\:1\:\:\:\:for\:all\:\:k$$
Change of weight for the winner
If a neuron does not respond to the input pattern, then no learning takes place in that neuron. However, if a particular neuron wins, then the corresponding weights are adjusted as follows −
$$\Delta w_{kj}\:=\:\begin{cases}-\alpha(x_{j}\:-\:w_{kj}), & if\:neuron\:k\:wins\\0 & if\:neuron\:k\:losses\end{cases}$$
Here $\alpha$ is the learning rate.
This clearly shows that we are favoring the winning neuron by adjusting its weight and if a neuron is lost, then we need not bother to re-adjust its weight.
K-means Clustering Algorithm
K-means is one of the most popular clustering algorithm in which we use the concept of partition procedure. We start with an initial partition and repeatedly move patterns from one cluster to another, until we get a satisfactory result.
Algorithm
Step 1 − Select k points as the initial centroids. Initialize k prototypes (w1,,wk), for example we can identifying them with randomly chosen input vectors −
$$W_{j}\:=\:i_{p},\:\:\: where\:j\:\in \lbrace1,....,k\rbrace\:and\:p\:\in \lbrace1,....,n\rbrace$$
Each cluster Cj is associated with prototype wj.
Step 2 − Repeat step 3-5 until E no longer decreases, or the cluster membership no longer changes.
Step 3 − For each input vector ip where p ∈ {1,,n}, put ip in the cluster Cj* with the nearest prototype wj* having the following relation
$$|i_{p}\:-\:w_{j*}|\:\leq\:|i_{p}\:-\:w_{j}|,\:j\:\in \lbrace1,....,k\rbrace$$
Step 4 − For each cluster Cj, where j ∈ { 1,,k}, update the prototype wj to be the centroid of all samples currently in Cj , so that
$$w_{j}\:=\:\sum_{i_{p}\in C_{j}}\frac{i_{p}}{|C_{j}|}$$
Step 5 − Compute the total quantization error as follows −
$$E\:=\:\sum_{j=1}^k\sum_{i_{p}\in w_{j}}|i_{p}\:-\:w_{j}|^2$$
Neocognitron
It is a multilayer feedforward network, which was developed by Fukushima in 1980s. This model is based on supervised learning and is used for visual pattern recognition, mainly hand-written characters. It is basically an extension of Cognitron network, which was also developed by Fukushima in 1975.
Architecture
It is a hierarchical network, which comprises many layers and there is a pattern of connectivity locally in those layers.
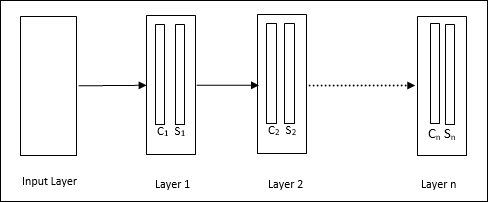
As we have seen in the above diagram, neocognitron is divided into different connected layers and each layer has two cells. Explanation of these cells is as follows −
S-Cell − It is called a simple cell, which is trained to respond to a particular pattern or a group of patterns.
C-Cell − It is called a complex cell, which combines the output from S-cell and simultaneously lessens the number of units in each array. In another sense, C-cell displaces the result of S-cell.
Training Algorithm
Training of neocognitron is found to be progressed layer by layer. The weights from the input layer to the first layer are trained and frozen. Then, the weights from the first layer to the second layer are trained, and so on. The internal calculations between S-cell and Ccell depend upon the weights coming from the previous layers. Hence, we can say that the training algorithm depends upon the calculations on S-cell and C-cell.
Calculations in S-cell
The S-cell possesses the excitatory signal received from the previous layer and possesses inhibitory signals obtained within the same layer.
$$\theta=\:\sqrt{\sum\sum t_{i} c_{i}^2}$$
Here, ti is the fixed weight and ci is the output from C-cell.
The scaled input of S-cell can be calculated as follows −
$$x\:=\:\frac{1\:+\:e}{1\:+\:vw_{0}}\:-\:1$$
Here, $e\:=\:\sum_i c_{i}w_{i}$
wi is the weight adjusted from C-cell to S-cell.
w0 is the weight adjustable between the input and S-cell.
v is the excitatory input from C-cell.
The activation of the output signal is,
$$s\:=\:\begin{cases}x, & if\:x \geq 0\\0, & if\:x
Calculations in C-cell
The net input of C-layer is
$$C\:=\:\displaystyle\sum\limits_i s_{i}x_{i}$$
Here, si is the output from S-cell and xi is the fixed weight from S-cell to C-cell.
The final output is as follows −
$$C_{out}\:=\:\begin{cases}\frac{C}{a+C}, & if\:C > 0\\0, & otherwise\end{cases}$$
Here a is the parameter that depends on the performance of the network.
Learning Vector Quantization
Learning Vector Quantization (LVQ), different from Vector quantization (VQ) and Kohonen Self-Organizing Maps (KSOM), basically is a competitive network which uses supervised learning. We may define it as a process of classifying the patterns where each output unit represents a class. As it uses supervised learning, the network will be given a set of training patterns with known classification along with an initial distribution of the output class. After completing the training process, LVQ will classify an input vector by assigning it to the same class as that of the output unit.
Architecture
Following figure shows the architecture of LVQ which is quite similar to the architecture of KSOM. As we can see, there are n number of input units and m number of output units. The layers are fully interconnected with having weights on them.
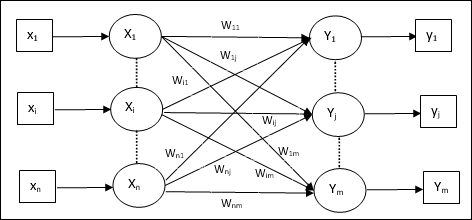
Parameters Used
Following are the parameters used in LVQ training process as well as in the flowchart
x = training vector (x1,...,xi,...,xn)
T = class for training vector x
wj = weight vector for jth output unit
Cj = class associated with the jth output unit
Training Algorithm
Step 1 − Initialize reference vectors, which can be done as follows −
Step 1(a) − From the given set of training vectors, take the first m (number of clusters) training vectors and use them as weight vectors. The remaining vectors can be used for training.
Step 1(b) − Assign the initial weight and classification randomly.
Step 1(c) − Apply K-means clustering method.
Step 2 − Initialize reference vector $\alpha$
Step 3 − Continue with steps 4-9, if the condition for stopping this algorithm is not met.
Step 4 − Follow steps 5-6 for every training input vector x.
Step 5 − Calculate Square of Euclidean Distance for j = 1 to m and i = 1 to n
$$D(j)\:=\:\displaystyle\sum\limits_{i=1}^n\displaystyle\sum\limits_{j=1}^m (x_{i}\:-\:w_{ij})^2$$
Step 6 − Obtain the winning unit J where D(j) is minimum.
Step 7 − Calculate the new weight of the winning unit by the following relation −
if T = Cj then $w_{j}(new)\:=\:w_{j}(old)\:+\:\alpha[x\:-\:w_{j}(old)]$
if T ≠ Cj then $w_{j}(new)\:=\:w_{j}(old)\:-\:\alpha[x\:-\:w_{j}(old)]$
Step 8 − Reduce the learning rate $\alpha$.
Step 9 − Test for the stopping condition. It may be as follows −
- Maximum number of epochs reached.
- Learning rate reduced to a negligible value.
Flowchart
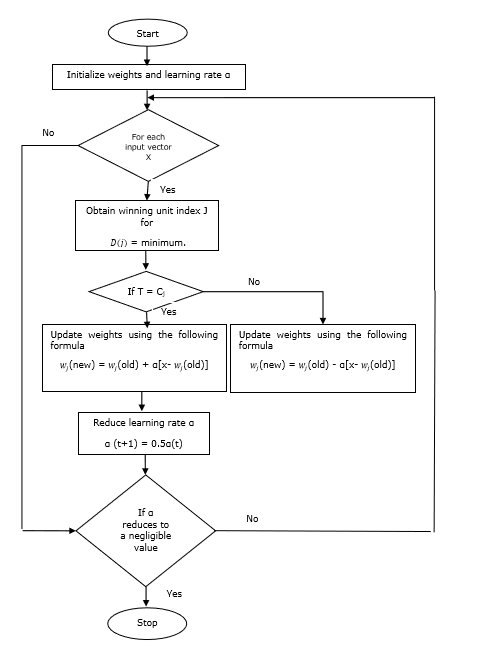
Variants
Three other variants namely LVQ2, LVQ2.1 and LVQ3 have been developed by Kohonen. Complexity in all these three variants, due to the concept that the winner as well as the runner-up unit will learn, is more than in LVQ.
LVQ2
As discussed, the concept of other variants of LVQ above, the condition of LVQ2 is formed by window. This window will be based on the following parameters −
x − the current input vector
yc − the reference vector closest to x
yr − the other reference vector, which is next closest to x
dc − the distance from x to yc
dr − the distance from x to yr
The input vector x falls in the window, if
$$\frac{d_{c}}{d_{r}}\:>\:1\:-\:\theta\:\:and\:\:\frac{d_{r}}{d_{c}}\:>\:1\:+\:\theta$$
Here, $\theta$ is the number of training samples.
Updating can be done with the following formula −
$y_{c}(t\:+\:1)\:=\:y_{c}(t)\:+\:\alpha(t)[x(t)\:-\:y_{c}(t)]$ (belongs to different class)
$y_{r}(t\:+\:1)\:=\:y_{r}(t)\:+\:\alpha(t)[x(t)\:-\:y_{r}(t)]$ (belongs to same class)
Here $\alpha$ is the learning rate.
LVQ2.1
In LVQ2.1, we will take the two closest vectors namely yc1 and yc2 and the condition for window is as follows −
$$Min\begin{bmatrix}\frac{d_{c1}}{d_{c2}},\frac{d_{c2}}{d_{c1}}\end{bmatrix}\:>\:(1\:-\:\theta)$$
$$Max\begin{bmatrix}\frac{d_{c1}}{d_{c2}},\frac{d_{c2}}{d_{c1}}\end{bmatrix}\:
Updating can be done with the following formula −
$y_{c1}(t\:+\:1)\:=\:y_{c1}(t)\:+\:\alpha(t)[x(t)\:-\:y_{c1}(t)]$ (belongs to different class)
$y_{c2}(t\:+\:1)\:=\:y_{c2}(t)\:+\:\alpha(t)[x(t)\:-\:y_{c2}(t)]$ (belongs to same class)
Here, $\alpha$ is the learning rate.
LVQ3
In LVQ3, we will take the two closest vectors namely yc1 and yc2 and the condition for window is as follows −
$$Min\begin{bmatrix}\frac{d_{c1}}{d_{c2}},\frac{d_{c2}}{d_{c1}}\end{bmatrix}\:>\:(1\:-\:\theta)(1\:+\:\theta)$$
Here $\theta\approx 0.2$
Updating can be done with the following formula −
$y_{c1}(t\:+\:1)\:=\:y_{c1}(t)\:+\:\beta(t)[x(t)\:-\:y_{c1}(t)]$ (belongs to different class)
$y_{c2}(t\:+\:1)\:=\:y_{c2}(t)\:+\:\beta(t)[x(t)\:-\:y_{c2}(t)]$ (belongs to same class)
Here $\beta$ is the multiple of the learning rate $\alpha$ and $\beta\:=\:m \alpha(t)$ for every 0.1 < m < 0.5
Adaptive Resonance Theory
This network was developed by Stephen Grossberg and Gail Carpenter in 1987. It is based on competition and uses unsupervised learning model. Adaptive Resonance Theory (ART) networks, as the name suggests, is always open to new learning (adaptive) without losing the old patterns (resonance). Basically, ART network is a vector classifier which accepts an input vector and classifies it into one of the categories depending upon which of the stored pattern it resembles the most.
Operating Principal
The main operation of ART classification can be divided into the following phases −
Recognition phase − The input vector is compared with the classification presented at every node in the output layer. The output of the neuron becomes 1 if it best matches with the classification applied, otherwise it becomes 0.
Comparison phase − In this phase, a comparison of the input vector to the comparison layer vector is done. The condition for reset is that the degree of similarity would be less than vigilance parameter.
Search phase − In this phase, the network will search for reset as well as the match done in the above phases. Hence, if there would be no reset and the match is quite good, then the classification is over. Otherwise, the process would be repeated and the other stored pattern must be sent to find the correct match.
ART1
It is a type of ART, which is designed to cluster binary vectors. We can understand about this with the architecture of it.
Architecture of ART1
It consists of the following two units −
Computational Unit − It is made up of the following −
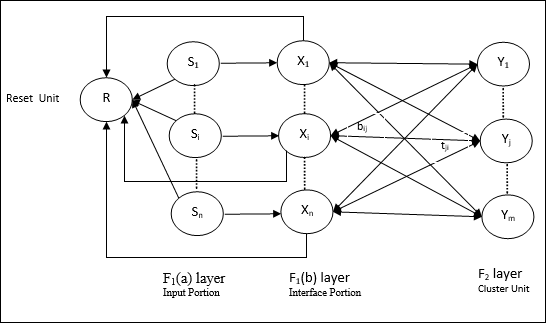
Input unit (F1 layer) − It further has the following two portions −
F1(a) layer (Input portion) − In ART1, there would be no processing in this portion rather than having the input vectors only. It is connected to F1(b) layer (interface portion).
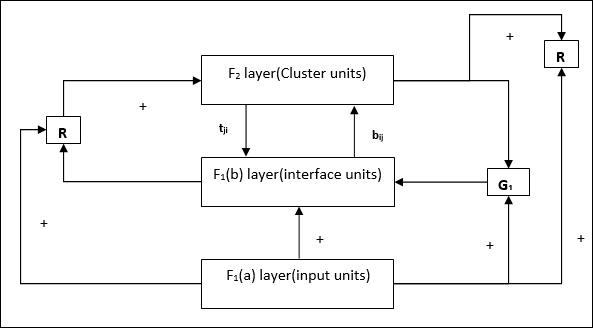
F1(b) layer (Interface portion) − This portion combines the signal from the input portion with that of F2 layer. F1(b) layer is connected to F2 layer through bottom up weights bij and F2 layer is connected to F1(b) layer through top down weights tji.
Cluster Unit (F2 layer) − This is a competitive layer. The unit having the largest net input is selected to learn the input pattern. The activation of all other cluster unit are set to 0.
Reset Mechanism − The work of this mechanism is based upon the similarity between the top-down weight and the input vector. Now, if the degree of this similarity is less than the vigilance parameter, then the cluster is not allowed to learn the pattern and a rest would happen.
Supplement Unit − Actually the issue with Reset mechanism is that the layer F2 must have to be inhibited under certain conditions and must also be available when some learning happens. That is why two supplemental units namely, G1 and G2 is added along with reset unit, R. They are called gain control units. These units receive and send signals to the other units present in the network. + indicates an excitatory signal, while − indicates an inhibitory signal.
Parameters Used
Following parameters are used −
n − Number of components in the input vector
m − Maximum number of clusters that can be formed
bij − Weight from F1(b) to F2 layer, i.e. bottom-up weights
tji − Weight from F2 to F1(b) layer, i.e. top-down weights
ρ − Vigilance parameter
||x|| − Norm of vector x
Algorithm
Step 1 − Initialize the learning rate, the vigilance parameter, and the weights as follows −
$$\alpha\:>\:1\:\:and\:\:0\:
$$0\:
Step 2 − Continue step 3-9, when the stopping condition is not true.
Step 3 − Continue step 4-6 for every training input.
Step 4 − Set activations of all F1(a) and F1 units as follows
F2 = 0 and F1(a) = input vectors
Step 5 − Input signal from F1(a) to F1(b) layer must be sent like
$$s_{i}\:=\:x_{i}$$
Step 6 − For every inhibited F2 node
$y_{j}\:=\:\sum_i b_{ij}x_{i}$ the condition is yj ≠ -1
Step 7 − Perform step 8-10, when the reset is true.
Step 8 − Find J for yJ ≥ yj for all nodes j
Step 9 − Again calculate the activation on F1(b) as follows
$$x_{i}\:=\:sitJi$$
Step 10 − Now, after calculating the norm of vector x and vector s, we need to check the reset condition as follows −
If ||x||/ ||s|| < vigilance parameter ρ,theninhibit node J and go to step 7
Else If ||x||/ ||s|| ≥ vigilance parameter ρ, then proceed further.
Step 11 − Weight updating for node J can be done as follows −
$$b_{ij}(new)\:=\:\frac{\alpha x_{i}}{\alpha\:-\:1\:+\:||x||}$$
$$t_{ij}(new)\:=\:x_{i}$$
Step 12 − The stopping condition for algorithm must be checked and it may be as follows −
- Do not have any change in weight.
- Reset is not performed for units.
- Maximum number of epochs reached.
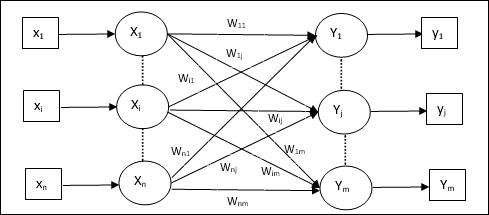
Kohonen Self-Organizing Feature Maps
Suppose we have some pattern of arbitrary dimensions, however, we need them in one dimension or two dimensions. Then the process of feature mapping would be very useful to convert the wide pattern space into a typical feature space. Now, the question arises why do we require self-organizing feature map? The reason is, along with the capability to convert the arbitrary dimensions into 1-D or 2-D, it must also have the ability to preserve the neighbor topology.
Neighbor Topologies in Kohonen SOM
There can be various topologies, however the following two topologies are used the most −
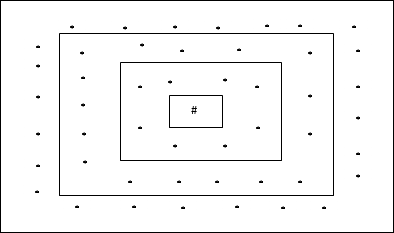
Rectangular Grid Topology
This topology has 24 nodes in the distance-2 grid, 16 nodes in the distance-1 grid, and 8 nodes in the distance-0 grid, which means the difference between each rectangular grid is 8 nodes. The winning unit is indicated by #.
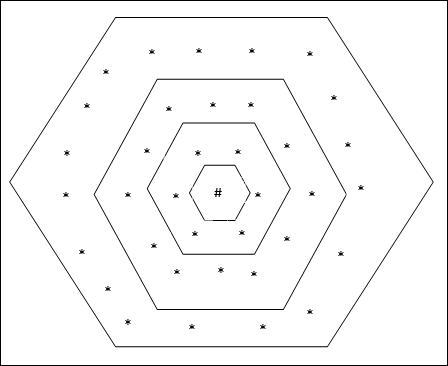
Hexagonal Grid Topology
This topology has 18 nodes in the distance-2 grid, 12 nodes in the distance-1 grid, and 6 nodes in the distance-0 grid, which means the difference between each rectangular grid is 6 nodes. The winning unit is indicated by #.
Architecture
The architecture of KSOM is similar to that of the competitive network. With the help of neighborhood schemes, discussed earlier, the training can take place over the extended region of the network.
Algorithm for training
Step 1 − Initialize the weights, the learning rate α and the neighborhood topological scheme.
Step 2 − Continue step 3-9, when the stopping condition is not true.
Step 3 − Continue step 4-6 for every input vector x.
Step 4 − Calculate Square of Euclidean Distance for j = 1 to m
$$D(j)\:=\:\displaystyle\sum\limits_{i=1}^n \displaystyle\sum\limits_{j=1}^m (x_{i}\:-\:w_{ij})^2$$
Step 5 − Obtain the winning unit J where D(j) is minimum.
Step 6 − Calculate the new weight of the winning unit by the following relation −
$$w_{ij}(new)\:=\:w_{ij}(old)\:+\:\alpha[x_{i}\:-\:w_{ij}(old)]$$
Step 7 − Update the learning rate α by the following relation −
$$\alpha(t\:+\:1)\:=\:0.5\alpha t$$
Step 8 − Reduce the radius of topological scheme.
Step 9 − Check for the stopping condition for the network.
Associate Memory Network
These kinds of neural networks work on the basis of pattern association, which means they can store different patterns and at the time of giving an output they can produce one of the stored patterns by matching them with the given input pattern. These types of memories are also called Content-Addressable Memory (CAM). Associative memory makes a parallel search with the stored patterns as data files.
Following are the two types of associative memories we can observe −
- Auto Associative Memory
- Hetero Associative memory
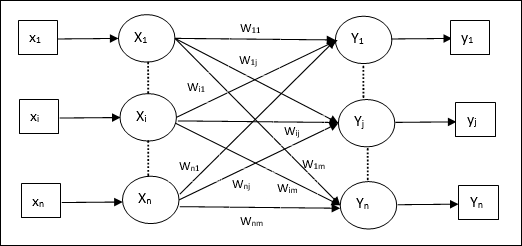
Auto Associative Memory
This is a single layer neural network in which the input training vector and the output target vectors are the same. The weights are determined so that the network stores a set of patterns.
Architecture
As shown in the following figure, the architecture of Auto Associative memory network has n number of input training vectors and similar n number of output target vectors.
Training Algorithm
For training, this network is using the Hebb or Delta learning rule.
Step 1 − Initialize all the weights to zero as wij = 0 (i = 1 to n, j = 1 to n)
Step 2 − Perform steps 3-4 for each input vector.
Step 3 − Activate each input unit as follows −
$$x_{i}\:=\:s_{i}\:(i\:=\:1\:to\:n)$$
Step 4 − Activate each output unit as follows −
$$y_{j}\:=\:s_{j}\:(j\:=\:1\:to\:n)$$
Step 5 − Adjust the weights as follows −
$$w_{ij}(new)\:=\:w_{ij}(old)\:+\:x_{i}y_{j}$$
Testing Algorithm
Step 1 − Set the weights obtained during training for Hebbs rule.
Step 2 − Perform steps 3-5 for each input vector.
Step 3 − Set the activation of the input units equal to that of the input vector.
Step 4 − Calculate the net input to each output unit j = 1 to n
$$y_{inj}\:=\:\displaystyle\sum\limits_{i=1}^n x_{i}w_{ij}$$
Step 5 − Apply the following activation function to calculate the output
$$y_{j}\:=\:f(y_{inj})\:=\:\begin{cases}+1 & if\:y_{inj}\:>\:0\\-1 & if\:y_{inj}\:\leqslant\:0\end{cases}$$
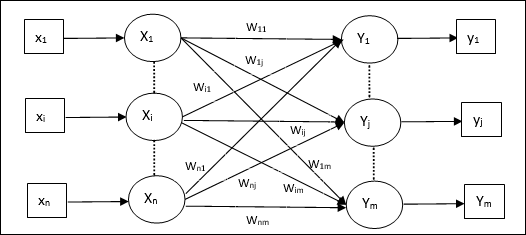
Hetero Associative memory
Similar to Auto Associative Memory network, this is also a single layer neural network. However, in this network the input training vector and the output target vectors are not the same. The weights are determined so that the network stores a set of patterns. Hetero associative network is static in nature, hence, there would be no non-linear and delay operations.
Architecture
As shown in the following figure, the architecture of Hetero Associative Memory network has n number of input training vectors and m number of output target vectors.
Training Algorithm
For training, this network is using the Hebb or Delta learning rule.
Step 1 − Initialize all the weights to zero as wij = 0 (i = 1 to n, j = 1 to m)
Step 2 − Perform steps 3-4 for each input vector.
Step 3 − Activate each input unit as follows −
$$x_{i}\:=\:s_{i}\:(i\:=\:1\:to\:n)$$
Step 4 − Activate each output unit as follows −
$$y_{j}\:=\:s_{j}\:(j\:=\:1\:to\:m)$$
Step 5 − Adjust the weights as follows −
$$w_{ij}(new)\:=\:w_{ij}(old)\:+\:x_{i}y_{j}$$
Testing Algorithm
Step 1 − Set the weights obtained during training for Hebbs rule.
Step 2 − Perform steps 3-5 for each input vector.
Step 3 − Set the activation of the input units equal to that of the input vector.
Step 4 − Calculate the net input to each output unit j = 1 to m;
$$y_{inj}\:=\:\displaystyle\sum\limits_{i=1}^n x_{i}w_{ij}$$
Step 5 − Apply the following activation function to calculate the output
$$y_{j}\:=\:f(y_{inj})\:=\:\begin{cases}+1 & if\:y_{inj}\:>\:0\\0 & if\:y_{inj}\:=\:0\\-1 & if\:y_{inj}\:
Artificial Neural Network - Hopfield Networks
Hopfield neural network was invented by Dr. John J. Hopfield in 1982. It consists of a single layer which contains one or more fully connected recurrent neurons. The Hopfield network is commonly used for auto-association and optimization tasks.
Discrete Hopfield Network
A Hopfield network which operates in a discrete line fashion or in other words, it can be said the input and output patterns are discrete vector, which can be either binary (0,1) or bipolar (+1, -1) in nature. The network has symmetrical weights with no self-connections i.e., wij = wji and wii = 0.
Architecture
Following are some important points to keep in mind about discrete Hopfield network −
This model consists of neurons with one inverting and one non-inverting output.
The output of each neuron should be the input of other neurons but not the input of self.
Weight/connection strength is represented by wij.
Connections can be excitatory as well as inhibitory. It would be excitatory, if the output of the neuron is same as the input, otherwise inhibitory.
Weights should be symmetrical, i.e. wij = wji
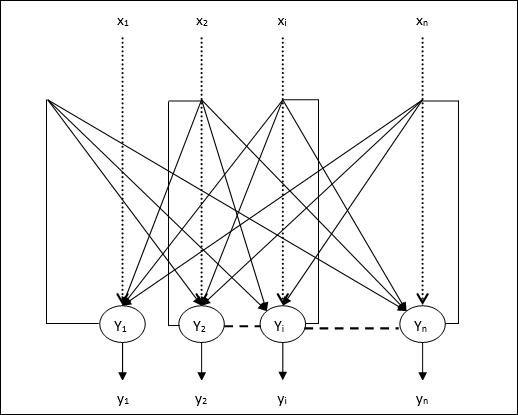
The output from Y1 going to Y2, Yi and Yn have the weights w12, w1i and w1n respectively. Similarly, other arcs have the weights on them.
Training Algorithm
During training of discrete Hopfield network, weights will be updated. As we know that we can have the binary input vectors as well as bipolar input vectors. Hence, in both the cases, weight updates can be done with the following relation
Case 1 − Binary input patterns
For a set of binary patterns s(p), p = 1 to P
Here, s(p) = s1(p), s2(p),..., si(p),..., sn(p)
Weight Matrix is given by
$$w_{ij}\:=\:\sum_{p=1}^P[2s_{i}(p)-\:1][2s_{j}(p)-\:1]\:\:\:\:\:for\:i\:\neq\:j$$
Case 2 − Bipolar input patterns
For a set of binary patterns s(p), p = 1 to P
Here, s(p) = s1(p), s2(p),..., si(p),..., sn(p)
Weight Matrix is given by
$$w_{ij}\:=\:\sum_{p=1}^P[s_{i}(p)][s_{j}(p)]\:\:\:\:\:for\:i\:\neq\:j$$
Testing Algorithm
Step 1 − Initialize the weights, which are obtained from training algorithm by using Hebbian principle.
Step 2 − Perform steps 3-9, if the activations of the network is not consolidated.
Step 3 − For each input vector X, perform steps 4-8.
Step 4 − Make initial activation of the network equal to the external input vector X as follows −
$$y_{i}\:=\:x_{i}\:\:\:for\:i\:=\:1\:to\:n$$
Step 5 − For each unit Yi, perform steps 6-9.
Step 6 − Calculate the net input of the network as follows −
$$y_{ini}\:=\:x_{i}\:+\:\displaystyle\sum\limits_{j}y_{j}w_{ji}$$
Step 7 − Apply the activation as follows over the net input to calculate the output −
$$y_{i}\:=\begin{cases}1 & if\:y_{ini}\:>\:\theta_{i}\\y_{i} & if\:y_{ini}\:=\:\theta_{i}\\0 & if\:y_{ini}\:
Here $\theta_{i}$ is the threshold.
Step 8 − Broadcast this output yi to all other units.
Step 9 − Test the network for conjunction.
Energy Function Evaluation
An energy function is defined as a function that is bonded and non-increasing function of the state of the system.
Energy function Ef, also called Lyapunov function determines the stability of discrete Hopfield network, and is characterized as follows −
$$E_{f}\:=\:-\frac{1}{2}\displaystyle\sum\limits_{i=1}^n\displaystyle\sum\limits_{j=1}^n y_{i}y_{j}w_{ij}\:-\:\displaystyle\sum\limits_{i=1}^n x_{i}y_{i}\:+\:\displaystyle\sum\limits_{i=1}^n \theta_{i}y_{i}$$
Condition − In a stable network, whenever the state of node changes, the above energy function will decrease.
Suppose when node i has changed state from $y_i^{(k)}$ to $y_i^{(k\:+\:1)}$ then the Energy change $\Delta E_{f}$ is given by the following relation
$$\Delta E_{f}\:=\:E_{f}(y_i^{(k+1)})\:-\:E_{f}(y_i^{(k)})$$
$$=\:-\left(\begin{array}{c}\displaystyle\sum\limits_{j=1}^n w_{ij}y_i^{(k)}\:+\:x_{i}\:-\:\theta_{i}\end{array}\right)(y_i^{(k+1)}\:-\:y_i^{(k)})$$
$$=\:-\:(net_{i})\Delta y_{i}$$
Here $\Delta y_{i}\:=\:y_i^{(k\:+\:1)}\:-\:y_i^{(k)}$
The change in energy depends on the fact that only one unit can update its activation at a time.
Continuous Hopfield Network
In comparison with Discrete Hopfield network, continuous network has time as a continuous variable. It is also used in auto association and optimization problems such as travelling salesman problem.
Model − The model or architecture can be build up by adding electrical components such as amplifiers which can map the input voltage to the output voltage over a sigmoid activation function.
Energy Function Evaluation
$$E_f = \frac{1}{2}\displaystyle\sum\limits_{i=1}^n\sum_{\substack{j = 1\\ j \ne i}}^n y_i y_j w_{ij} - \displaystyle\sum\limits_{i=1}^n x_i y_i + \frac{1}{\lambda} \displaystyle\sum\limits_{i=1}^n \sum_{\substack{j = 1\\ j \ne i}}^n w_{ij} g_{ri} \int_{0}^{y_i} a^{-1}(y) dy$$
Here λ is gain parameter and gri input conductance.
Boltzmann Machine
These are stochastic learning processes having recurrent structure and are the basis of the early optimization techniques used in ANN. Boltzmann Machine was invented by Geoffrey Hinton and Terry Sejnowski in 1985. More clarity can be observed in the words of Hinton on Boltzmann Machine.
A surprising feature of this network is that it uses only locally available information. The change of weight depends only on the behavior of the two units it connects, even though the change optimizes a global measure - Ackley, Hinton 1985.
Some important points about Boltzmann Machine −
They use recurrent structure.
They consist of stochastic neurons, which have one of the two possible states, either 1 or 0.
Some of the neurons in this are adaptive (free state) and some are clamped (frozen state).
If we apply simulated annealing on discrete Hopfield network, then it would become Boltzmann Machine.
Objective of Boltzmann Machine
The main purpose of Boltzmann Machine is to optimize the solution of a problem. It is the work of Boltzmann Machine to optimize the weights and quantity related to that particular problem.
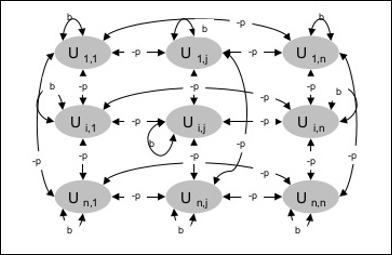
Architecture
The following diagram shows the architecture of Boltzmann machine. It is clear from the diagram, that it is a two-dimensional array of units. Here, weights on interconnections between units are p where p > 0. The weights of self-connections are given by b where b > 0.
Training Algorithm
As we know that Boltzmann machines have fixed weights, hence there will be no training algorithm as we do not need to update the weights in the network. However, to test the network we have to set the weights as well as to find the consensus function (CF).
Boltzmann machine has a set of units Ui and Uj and has bi-directional connections on them.
We are considering the fixed weight say wij.
wij ≠ 0 if Ui and Uj are connected.
There also exists a symmetry in weighted interconnection, i.e. wij = wji.
wii also exists, i.e. there would be the self-connection between units.
For any unit Ui, its state ui would be either 1 or 0.
The main objective of Boltzmann Machine is to maximize the Consensus Function (CF) which can be given by the following relation
$$CF\:=\:\displaystyle\sum\limits_{i} \displaystyle\sum\limits_{j\leqslant i} w_{ij}u_{i}u_{j}$$
Now, when the state changes from either 1 to 0 or from 0 to 1, then the change in consensus can be given by the following relation −
$$\Delta CF\:=\:(1\:-\:2u_{i})(w_{ij}\:+\:\displaystyle\sum\limits_{j\neq i} u_{i} w_{ij})$$
Here ui is the current state of Ui.
The variation in coefficient (1 - 2ui) is given by the following relation −
$$(1\:-\:2u_{i})\:=\:\begin{cases}+1, & U_{i}\:is\:currently\:off\\-1, & U_{i}\:is\:currently\:on\end{cases}$$
Generally, unit Ui does not change its state, but if it does then the information would be residing local to the unit. With that change, there would also be an increase in the consensus of the network.
Probability of the network to accept the change in the state of the unit is given by the following relation −
$$AF(i,T)\:=\:\frac{1}{1\:+\:exp[-\frac{\Delta CF(i)}{T}]}$$
Here, T is the controlling parameter. It will decrease as CF reaches the maximum value.
Testing Algorithm
Step 1 − Initialize the following to start the training −
- Weights representing the constraint of the problem
- Control Parameter T
Step 2 − Continue steps 3-8, when the stopping condition is not true.
Step 3 − Perform steps 4-7.
Step 4 − Assume that one of the state has changed the weight and choose the integer I, J as random values between 1 and n.
Step 5 − Calculate the change in consensus as follows −
$$\Delta CF\:=\:(1\:-\:2u_{i})(w_{ij}\:+\:\displaystyle\sum\limits_{j\neq i} u_{i} w_{ij})$$
Step 6 − Calculate the probability that this network would accept the change in state
$$AF(i,T)\:=\:\frac{1}{1\:+\:exp[-\frac{\Delta CF(i)}{T}]}$$
Step 7 − Accept or reject this change as follows −
Case I − if R < AF, accept the change.
Case II − if R ≥ AF, reject the change.
Here, R is the random number between 0 and 1.
Step 8 − Reduce the control parameter (temperature) as follows −
T(new) = 0.95T(old)
Step 9 − Test for the stopping conditions which may be as follows −
- Temperature reaches a specified value
- There is no change in state for a specified number of iterations
Brain-State-in-a-Box Network
The Brain-State-in-a-Box (BSB) neural network is a nonlinear auto-associative neural network and can be extended to hetero-association with two or more layers. It is also similar to Hopfield network. It was proposed by J.A. Anderson, J.W. Silverstein, S.A. Ritz and R.S. Jones in 1977.
Some important points to remember about BSB Network −
It is a fully connected network with the maximum number of nodes depending upon the dimensionality n of the input space.
All the neurons are updated simultaneously.
Neurons take values between -1 to +1.
Mathematical Formulations
The node function used in BSB network is a ramp function, which can be defined as follows −
$$f(net)\:=\:min(1,\:max(-1,\:net))$$
This ramp function is bounded and continuous.
As we know that each node would change its state, it can be done with the help of the following mathematical relation −
$$x_{t}(t\:+\:1)\:=\:f\left(\begin{array}{c}\displaystyle\sum\limits_{j=1}^n w_{i,j}x_{j}(t)\end{array}\right)$$
Here, xi(t) is the state of the ith node at time t.
Weights from ith node to jth node can be measured with the following relation −
$$w_{ij}\:=\:\frac{1}{P}\displaystyle\sum\limits_{p=1}^P (v_{p,i}\:v_{p,j})$$
Here, P is the number of training patterns, which are bipolar.
Optimization Using Hopfield Network
Optimization is an action of making something such as design, situation, resource, and system as effective as possible. Using a resemblance between the cost function and energy function, we can use highly interconnected neurons to solve optimization problems. Such a kind of neural network is Hopfield network, that consists of a single layer containing one or more fully connected recurrent neurons. This can be used for optimization.
Points to remember while using Hopfield network for optimization −
The energy function must be minimum of the network.
It will find satisfactory solution rather than select one out of the stored patterns.
The quality of the solution found by Hopfield network depends significantly on the initial state of the network.
Travelling Salesman Problem
Finding the shortest route travelled by the salesman is one of the computational problems, which can be optimized by using Hopfield neural network.
Basic Concept of TSP
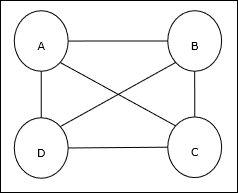
Travelling Salesman Problem (TSP) is a classical optimization problem in which a salesman has to travel n cities, which are connected with each other, keeping the cost as well as the distance travelled minimum. For example, the salesman has to travel a set of 4 cities A, B, C, D and the goal is to find the shortest circular tour, A-B-CD, so as to minimize the cost, which also includes the cost of travelling from the last city D to the first city A.
Matrix Representation
Actually each tour of n-city TSP can be expressed as n × n matrix whose ith row describes the ith citys location. This matrix, M, for 4 cities A, B, C, D can be expressed as follows −
$$M = \begin{bmatrix}A: & 1 & 0 & 0 & 0 \\B: & 0 & 1 & 0 & 0 \\C: & 0 & 0 & 1 & 0 \\D: & 0 & 0 & 0 & 1 \end{bmatrix}$$
Solution by Hopfield Network
While considering the solution of this TSP by Hopfield network, every node in the network corresponds to one element in the matrix.
Energy Function Calculation
To be the optimized solution, the energy function must be minimum. On the basis of the following constraints, we can calculate the energy function as follows −
Constraint-I
First constraint, on the basis of which we will calculate energy function, is that one element must be equal to 1 in each row of matrix M and other elements in each row must equal to 0 because each city can occur in only one position in the TSP tour. This constraint can mathematically be written as follows −
$$\displaystyle\sum\limits_{j=1}^n M_{x,j}\:=\:1\:for \: x\:\in \:\lbrace1,...,n\rbrace$$
Now the energy function to be minimized, based on the above constraint, will contain a term proportional to −
$$\displaystyle\sum\limits_{x=1}^n \left(\begin{array}{c}1\:-\:\displaystyle\sum\limits_{j=1}^n M_{x,j}\end{array}\right)^2$$
Constraint-II
As we know, in TSP one city can occur in any position in the tour hence in each column of matrix M, one element must equal to 1 and other elements must be equal to 0. This constraint can mathematically be written as follows −
$$\displaystyle\sum\limits_{x=1}^n M_{x,j}\:=\:1\:for \: j\:\in \:\lbrace1,...,n\rbrace$$
Now the energy function to be minimized, based on the above constraint, will contain a term proportional to −
$$\displaystyle\sum\limits_{j=1}^n \left(\begin{array}{c}1\:-\:\displaystyle\sum\limits_{x=1}^n M_{x,j}\end{array}\right)^2$$
Cost Function Calculation
Lets suppose a square matrix of (n × n) denoted by C denotes the cost matrix of TSP for n cities where n > 0. Following are some parameters while calculating the cost function −
Cx, y − The element of cost matrix denotes the cost of travelling from city x to y.
Adjacency of the elements of A and B can be shown by the following relation −
$$M_{x,i}\:=\:1\:\: and\:\: M_{y,i\pm 1}\:=\:1$$
As we know, in Matrix the output value of each node can be either 0 or 1, hence for every pair of cities A, B we can add the following terms to the energy function −
$$\displaystyle\sum\limits_{i=1}^n C_{x,y}M_{x,i}(M_{y,i+1}\:+\:M_{y,i-1})$$
On the basis of the above cost function and constraint value, the final energy function E can be given as follows −
$$E\:=\:\frac{1}{2}\displaystyle\sum\limits_{i=1}^n\displaystyle\sum\limits_{x}\displaystyle\sum\limits_{y\neq x}C_{x,y}M_{x,i}(M_{y,i+1}\:+\:M_{y,i-1})\:+$$
$$\:\begin{bmatrix}\gamma_{1} \displaystyle\sum\limits_{x} \left(\begin{array}{c}1\:-\:\displaystyle\sum\limits_{i} M_{x,i}\end{array}\right)^2\:+\: \gamma_{2} \displaystyle\sum\limits_{i} \left(\begin{array}{c}1\:-\:\displaystyle\sum\limits_{x} M_{x,i}\end{array}\right)^2 \end{bmatrix}$$
Here, γ1 and γ2 are two weighing constants.
Other Optimization Techniques
Iterated Gradient Descent Technique
Gradient descent, also known as the steepest descent, is an iterative optimization algorithm to find a local minimum of a function. While minimizing the function, we are concerned with the cost or error to be minimized (Remember Travelling Salesman Problem). It is extensively used in deep learning, which is useful in a wide variety of situations. The point here to be remembered is that we are concerned with local optimization and not global optimization.
Main Working Idea
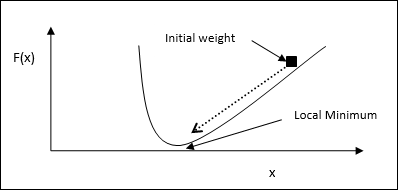
We can understand the main working idea of gradient descent with the help of the following steps −
First, start with an initial guess of the solution.
Then, take the gradient of the function at that point.
Later, repeat the process by stepping the solution in the negative direction of the gradient.
By following the above steps, the algorithm will eventually converge where the gradient is zero.
Mathematical Concept
Suppose we have a function f(x) and we are trying to find the minimum of this function. Following are the steps to find the minimum of f(x).
First, give some initial value $x_{0}\:for\:x$
Now take the gradient $\nabla f$ of function, with the intuition that the gradient will give the slope of the curve at that x and its direction will point to the increase in the function, to find out the best direction to minimize it.
Now change x as follows −
$$x_{n\:+\:1}\:=\:x_{n}\:-\:\theta \nabla f(x_{n})$$
Here, θ > 0 is the training rate (step size) that forces the algorithm to take small jumps.
Estimating Step Size
Actually a wrong step size θ may not reach convergence, hence a careful selection of the same is very important. Following points must have to be remembered while choosing the step size
Do not choose too large step size, otherwise it will have a negative impact, i.e. it will diverge rather than converge.
Do not choose too small step size, otherwise it take a lot of time to converge.
Some options with regards to choosing the step size −
One option is to choose a fixed step size.
Another option is to choose a different step size for every iteration.
Simulated Annealing
The basic concept of Simulated Annealing (SA) is motivated by the annealing in solids. In the process of annealing, if we heat a metal above its melting point and cool it down then the structural properties will depend upon the rate of cooling. We can also say that SA simulates the metallurgy process of annealing.
Use in ANN
SA is a stochastic computational method, inspired by Annealing analogy, for approximating the global optimization of a given function. We can use SA to train feed-forward neural networks.
Algorithm
Step 1 − Generate a random solution.
Step 2 − Calculate its cost using some cost function.
Step 3 − Generate a random neighboring solution.
Step 4 − Calculate the new solution cost by the same cost function.
Step 5 − Compare the cost of a new solution with that of an old solution as follows −
If CostNew Solution < CostOld Solution then move to the new solution.
Step 6 − Test for the stopping condition, which may be the maximum number of iterations reached or get an acceptable solution.
Artificial Neural Network - Genetic Algorithm
Nature has always been a great source of inspiration to all mankind. Genetic Algorithms (GAs) are search-based algorithms based on the concepts of natural selection and genetics. GAs are a subset of a much larger branch of computation known as Evolutionary Computation.
GAs was developed by John Holland and his students and colleagues at the University of Michigan, most notably David E. Goldberg and has since been tried on various optimization problems with a high degree of success.
In GAs, we have a pool or a population of possible solutions to the given problem. These solutions then undergo recombination and mutation (like in natural genetics), producing new children, and the process is repeated over various generations. Each individual (or candidate solution) is assigned a fitness value (based on its objective function value) and the fitter individuals are given a higher chance to mate and yield more fitter individuals. This is in line with the Darwinian Theory of Survival of the Fittest.
In this way, we keep evolving better individuals or solutions over generations, till we reach a stopping criterion.
Genetic Algorithms are sufficiently randomized in nature, however they perform much better than random local search (in which we just try various random solutions, keeping track of the best so far), as they exploit historical information as well.
Advantages of GAs
GAs have various advantages which have made them immensely popular. These include −
Does not require any derivative information (which may not be available for many real-world problems).
Is faster and more efficient as compared to the traditional methods.
Has very good parallel capabilities.
Optimizes both continuous and discrete functions as well as multi-objective problems.
Provides a list of good solutions and not just a single solution.
Always gets an answer to the problem, which gets better over the time.
Useful when the search space is very large and there are large number of parameters involved.
Limitations of GAs
Like any technique, GAs also suffers from a few limitations. These include −
GAs are not suited for all problems, especially problems which are simple and for which derivative information is available.
Fitness value is calculated repeatedly, which might be computationally expensive for some problems.
Being stochastic, there are no guarantees on the optimality or the quality of the solution.
If not implemented properly, GA may not converge to the optimal solution.
GA Motivation
Genetic Algorithms have the ability to deliver a good-enough solution fast-enough. This makes Gas attractive for use in solving optimization problems. The reasons why GAs are needed are as follows −
Solving Difficult Problems
In computer science, there is a large set of problems, which are NP-Hard. What this essentially means is that, even the most powerful computing systems take a very long time (even years!) to solve that problem. In such a scenario, GAs prove to be an efficient tool to provide usable near-optimal solutions in a short amount of time.
Failure of Gradient Based Methods
Traditional calculus based methods work by starting at a random point and by moving in the direction of the gradient, till we reach the top of the hill. This technique is efficient and works very well for single-peaked objective functions like the cost function in linear regression. However, in most real-world situations, we have a very complex problem called as landscapes, made of many peaks and many valleys, which causes such methods to fail, as they suffer from an inherent tendency of getting stuck at the local optima as shown in the following figure.
Getting a Good Solution Fast
Some difficult problems like the Travelling Salesman Problem (TSP), have real-world applications like path finding and VLSI Design. Now imagine that you are using your GPS Navigation system, and it takes a few minutes (or even a few hours) to compute the optimal path from the source to destination. Delay in such real-world applications is not acceptable and therefore a good-enough solution, which is delivered fast is what is required.
How to Use GA for Optimization Problems?
We already know that optimization is an action of making something such as design, situation, resource, and system as effective as possible. Optimization process is shown in the following diagram.

Stages of GA Mechanism for Optimization Process
Followings are the stages of GA mechanism when used for optimization of problems.
Generate the initial population randomly.
Select the initial solution with the best fitness values.
Recombine the selected solutions using mutation and crossover operators.
Insert offspring into the population.
Now if the stop condition is met, then return the solution with their best fitness value. Else, go to step 2.
Applications of Neural Networks
Before studying the fields where ANN has been used extensively, we need to understand why ANN would be the preferred choice of application.
Why Artificial Neural Networks?
We need to understand the answer to the above question with an example of a human being. As a child, we used to learn the things with the help of our elders, which includes our parents or teachers. Then later by self-learning or practice we keep learning throughout our life. Scientists and researchers are also making the machine intelligent, just like a human being, and ANN plays a very important role in the same due to the following reasons −
With the help of neural networks, we can find the solution of such problems for which algorithmic method is expensive or does not exist.
Neural networks can learn by example, hence we do not need to program it at much extent.
Neural networks have the accuracy and significantly fast speed than conventional speed.
Areas of Application
Followings are some of the areas, where ANN is being used. It suggests that ANN has an interdisciplinary approach in its development and applications.
Speech Recognition
Speech occupies a prominent role in human-human interaction. Therefore, it is natural for people to expect speech interfaces with computers. In the present era, for communication with machines, humans still need sophisticated languages which are difficult to learn and use. To ease this communication barrier, a simple solution could be, communication in a spoken language that is possible for the machine to understand.
Great progress has been made in this field, however, still such kinds of systems are facing the problem of limited vocabulary or grammar along with the issue of retraining of the system for different speakers in different conditions. ANN is playing a major role in this area. Following ANNs have been used for speech recognition −
Multilayer networks
Multilayer networks with recurrent connections
Kohonen self-organizing feature map
The most useful network for this is Kohonen Self-Organizing feature map, which has its input as short segments of the speech waveform. It will map the same kind of phonemes as the output array, called feature extraction technique. After extracting the features, with the help of some acoustic models as back-end processing, it will recognize the utterance.
Character Recognition
It is an interesting problem which falls under the general area of Pattern Recognition. Many neural networks have been developed for automatic recognition of handwritten characters, either letters or digits. Following are some ANNs which have been used for character recognition −
- Multilayer neural networks such as Backpropagation neural networks.
- Neocognitron
Though back-propagation neural networks have several hidden layers, the pattern of connection from one layer to the next is localized. Similarly, neocognitron also has several hidden layers and its training is done layer by layer for such kind of applications.
Signature Verification Application
Signatures are one of the most useful ways to authorize and authenticate a person in legal transactions. Signature verification technique is a non-vision based technique.
For this application, the first approach is to extract the feature or rather the geometrical feature set representing the signature. With these feature sets, we have to train the neural networks using an efficient neural network algorithm. This trained neural network will classify the signature as being genuine or forged under the verification stage.
Human Face Recognition
It is one of the biometric methods to identify the given face. It is a typical task because of the characterization of non-face images. However, if a neural network is well trained, then it can be divided into two classes namely images having faces and images that do not have faces.
First, all the input images must be preprocessed. Then, the dimensionality of that image must be reduced. And, at last it must be classified using neural network training algorithm. Following neural networks are used for training purposes with preprocessed image −
Fully-connected multilayer feed-forward neural network trained with the help of back-propagation algorithm.
For dimensionality reduction, Principal Component Analysis (PCA) is used.