
- Data Structures & Algorithms
- DSA - Home
- DSA - Overview
- DSA - Environment Setup
- DSA - Algorithms Basics
- DSA - Asymptotic Analysis
- Data Structures
- DSA - Data Structure Basics
- DSA - Data Structures and Types
- DSA - Array Data Structure
- Linked Lists
- DSA - Linked List Data Structure
- DSA - Doubly Linked List Data Structure
- DSA - Circular Linked List Data Structure
- Stack & Queue
- DSA - Stack Data Structure
- DSA - Expression Parsing
- DSA - Queue Data Structure
- Searching Algorithms
- DSA - Searching Algorithms
- DSA - Linear Search Algorithm
- DSA - Binary Search Algorithm
- DSA - Interpolation Search
- DSA - Jump Search Algorithm
- DSA - Exponential Search
- DSA - Fibonacci Search
- DSA - Sublist Search
- DSA - Hash Table
- Sorting Algorithms
- DSA - Sorting Algorithms
- DSA - Bubble Sort Algorithm
- DSA - Insertion Sort Algorithm
- DSA - Selection Sort Algorithm
- DSA - Merge Sort Algorithm
- DSA - Shell Sort Algorithm
- DSA - Heap Sort
- DSA - Bucket Sort Algorithm
- DSA - Counting Sort Algorithm
- DSA - Radix Sort Algorithm
- DSA - Quick Sort Algorithm
- Graph Data Structure
- DSA - Graph Data Structure
- DSA - Depth First Traversal
- DSA - Breadth First Traversal
- DSA - Spanning Tree
- Tree Data Structure
- DSA - Tree Data Structure
- DSA - Tree Traversal
- DSA - Binary Search Tree
- DSA - AVL Tree
- DSA - Red Black Trees
- DSA - B Trees
- DSA - B+ Trees
- DSA - Splay Trees
- DSA - Tries
- DSA - Heap Data Structure
- Recursion
- DSA - Recursion Algorithms
- DSA - Tower of Hanoi Using Recursion
- DSA - Fibonacci Series Using Recursion
- Divide and Conquer
- DSA - Divide and Conquer
- DSA - Max-Min Problem
- DSA - Strassen's Matrix Multiplication
- DSA - Karatsuba Algorithm
- Greedy Algorithms
- DSA - Greedy Algorithms
- DSA - Travelling Salesman Problem (Greedy Approach)
- DSA - Prim's Minimal Spanning Tree
- DSA - Kruskal's Minimal Spanning Tree
- DSA - Dijkstra's Shortest Path Algorithm
- DSA - Map Colouring Algorithm
- DSA - Fractional Knapsack Problem
- DSA - Job Sequencing with Deadline
- DSA - Optimal Merge Pattern Algorithm
- Dynamic Programming
- DSA - Dynamic Programming
- DSA - Matrix Chain Multiplication
- DSA - Floyd Warshall Algorithm
- DSA - 0-1 Knapsack Problem
- DSA - Longest Common Subsequence Algorithm
- DSA - Travelling Salesman Problem (Dynamic Approach)
- Approximation Algorithms
- DSA - Approximation Algorithms
- DSA - Vertex Cover Algorithm
- DSA - Set Cover Problem
- DSA - Travelling Salesman Problem (Approximation Approach)
- Randomized Algorithms
- DSA - Randomized Algorithms
- DSA - Randomized Quick Sort Algorithm
- DSA - Karger’s Minimum Cut Algorithm
- DSA - Fisher-Yates Shuffle Algorithm
- DSA Useful Resources
- DSA - Questions and Answers
- DSA - Quick Guide
- DSA - Useful Resources
- DSA - Discussion
Tree Data Structure
Tree Data Structrue
A tree is a non-linear abstract data type with a hierarchy-based structure. It consists of nodes (where the data is stored) that are connected via links. The tree data structure stems from a single node called a root node and has subtrees connected to the root.
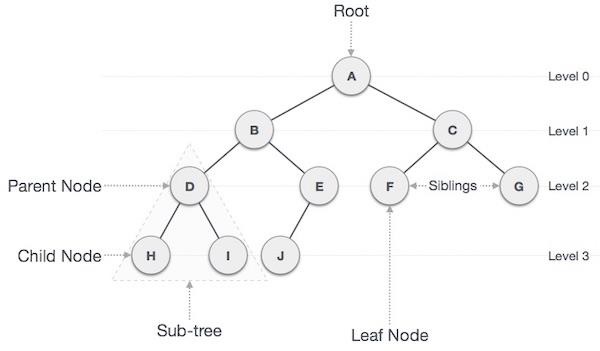
Important Terms
Following are the important terms with respect to tree.
Path − Path refers to the sequence of nodes along the edges of a tree.
Root − The node at the top of the tree is called root. There is only one root per tree and one path from the root node to any node.
Parent − Any node except the root node has one edge upward to a node called parent.
Child − The node below a given node connected by its edge downward is called its child node.
Leaf − The node which does not have any child node is called the leaf node.
Subtree − Subtree represents the descendants of a node.
Visiting − Visiting refers to checking the value of a node when control is on the node.
Traversing − Traversing means passing through nodes in a specific order.
Levels − Level of a node represents the generation of a node. If the root node is at level 0, then its next child node is at level 1, its grandchild is at level 2, and so on.
Keys − Key represents a value of a node based on which a search operation is to be carried out for a node.
Types of Trees
There are three types of trees −
General Trees
Binary Trees
Binary Search Trees
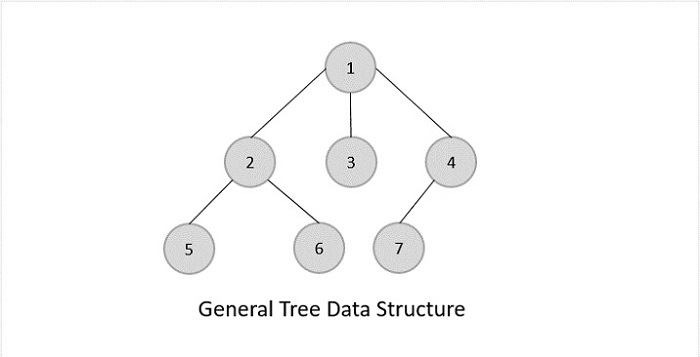
General Trees
General trees are unordered tree data structures where the root node has minimum 0 or maximum ‘n’ subtrees.
The General trees have no constraint placed on their hierarchy. The root node thus acts like the superset of all the other subtrees.
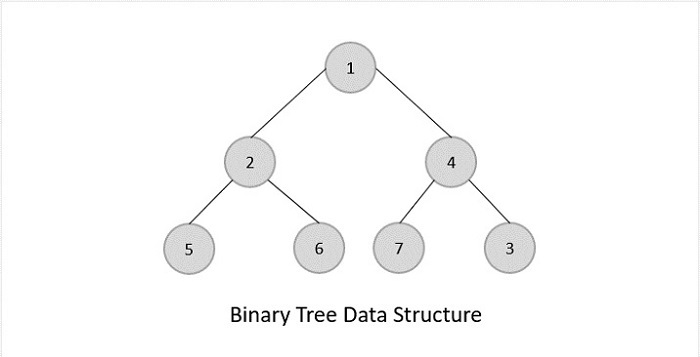
Binary Trees
Binary Trees are general trees in which the root node can only hold up to maximum 2 subtrees: left subtree and right subtree. Based on the number of children, binary trees are divided into three types.
Full Binary Tree
A full binary tree is a binary tree type where every node has either 0 or 2 child nodes.
Complete Binary Tree
A complete binary tree is a binary tree type where all the leaf nodes must be on the same level. However, root and internal nodes in a complete binary tree can either have 0, 1 or 2 child nodes.
Perfect Binary Tree
A perfect binary tree is a binary tree type where all the leaf nodes are on the same level and every node except leaf nodes have 2 children.
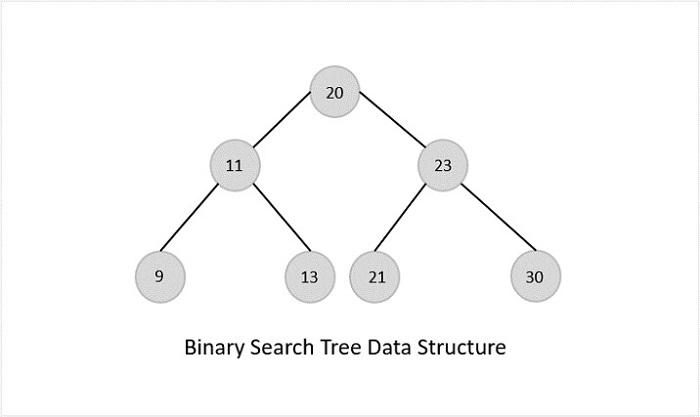
Binary Search Trees
Binary Search Trees possess all the properties of Binary Trees including some extra properties of their own, based on some constraints, making them more efficient than binary trees.
The data in the Binary Search Trees (BST) is always stored in such a way that the values in the left subtree are always less than the values in the root node and the values in the right subtree are always greater than the values in the root node, i.e. left subtree < root node ≤ right subtree.
Advantages of BST
Binary Search Trees are more efficient than Binary Trees since time complexity for performing various operations reduces.
Since the order of keys is based on just the parent node, searching operation becomes simpler.
The alignment of BST also favors Range Queries, which are executed to find values existing between two keys. This helps in the Database Management System.
Disadvantages of BST
The main disadvantage of Binary Search Trees is that if all elements in nodes are either greater than or lesser than the root node, the tree becomes skewed. Simply put, the tree becomes slanted to one side completely.
This skewness will make the tree a linked list rather than a BST, since the worst case time complexity for searching operation becomes O(n).
To overcome this issue of skewness in the Binary Search Trees, the concept of Balanced Binary Search Trees was introduced.
Balanced Binary Search Trees
Consider a Binary Search Tree with ‘m’ as the height of the left subtree and ‘n’ as the height of the right subtree. If the value of (m-n) is equal to 0,1 or -1, the tree is said to be a Balanced Binary Search Tree.
The trees are designed in a way that they self-balance once the height difference exceeds 1. Binary Search Trees use rotations as self-balancing algorithms. There are four different types of rotations: Left Left, Right Right, Left Right, Right Left.
There are various types of self-balancing binary search trees −
Priority Search Trees
