Tries Data Structure

Table of content
Previous
Quiz
Next

A trie is a type of a multi-way search tree, which is fundamentally used to retrieve specific keys from a string or a set of strings. It stores the data in an ordered efficient way since it uses pointers to every letter within the alphabet.

The trie data structure works based on the common prefixes of strings. The root node can have any number of nodes considering the amount of strings present in the set. The root of a trie does not contain any value except the pointers to its child nodes.

There are three types of trie data structures −

  • Standard Tries

  • Compressed Tries

  • Suffix Tries

The real-world applications of trie include − autocorrect, text prediction, sentiment analysis and data sciences.

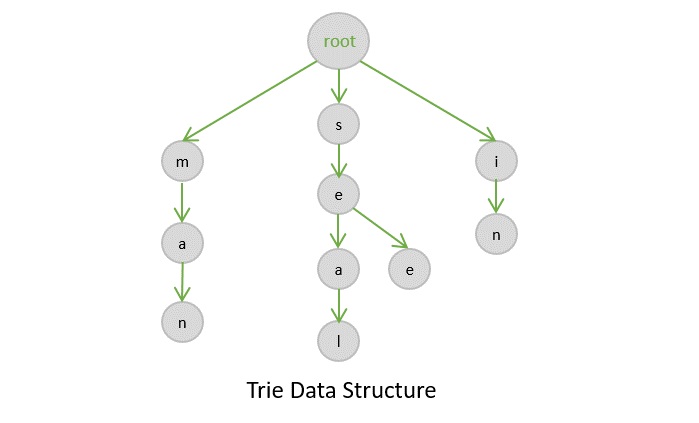
trie data structure

Basic Operations in Tries

The trie data structures also perform the same operations that tree data structures perform. They are −

  • Insertion

  • Deletion

  • Search

Insertion operation

The insertion operation in a trie is a simple approach. The root in a trie does not hold any value and the insertion starts from the immediate child nodes of the root, which act like a key to their child nodes. However, we observe that each node in a trie represents a singlecharacter in the input string. Hence the characters are added into the tries one by one while the links in the trie act as pointers to the next level nodes.

Example

Following are the implementations of this operation in various programming languages −

C C++ Java Python 
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#define ALPHABET_SIZE 26
struct TrieNode {
    struct TrieNode* children[ALPHABET_SIZE];
    int isEndOfWord;
};
struct Trie {
    struct TrieNode* root;
};
struct TrieNode* createNode() {
    struct TrieNode* node = (struct TrieNode*)malloc(sizeof(struct TrieNode));
    node->isEndOfWord = 0;
    for (int i = 0; i < ALPHABET_SIZE; i++) {
        node->children[i] = NULL;
    }
    return node;
}
void insert(struct Trie* trie, const char* key) {
    struct TrieNode* curr = trie->root;
    for (int i = 0; i < strlen(key); i++) {
        int index = key[i] - 'a';
        if (curr->children[index] == NULL) {
            curr->children[index] = createNode();
        }
        curr = curr->children[index];
    }
    curr->isEndOfWord = 1;
}

void printWords(struct TrieNode* node, char* prefix) {
    if (node->isEndOfWord) {
        printf("%s\n", prefix);
    }
    for (int i = 0; i < ALPHABET_SIZE; i++) {
        if (node->children[i] != NULL) {
            char* newPrefix = (char*)malloc(strlen(prefix) + 2);
            strcpy(newPrefix, prefix);
            newPrefix[strlen(prefix)] = 'A' + i;
            newPrefix[strlen(prefix) + 1] = '\0';
            printWords(node->children[i], newPrefix);
            free(newPrefix);
        }
    }
}
int main() {
    struct Trie car;
    car.root = createNode();
    insert(&car, "lamborghini");
    insert(&car, "mercedes-Benz");
    insert(&car, "land Rover");
    insert(&car, "maruti Suzuki");
    printf("Trie elements are:\n");
    printWords(car.root, "");
    return 0;
}

Output

Trie elements are:
LAMBORGHINI
LANDNOVER
MARUTIOUZUKI
MERCEZENZ

#include <iostream>
#include <unordered_map>
#include <string>
class TrieNode {
public:
   std::unordered_map<char, TrieNode*> children;
   bool isEndOfWord;
   
   TrieNode() {
      isEndOfWord = false;
   }
};
class Trie {
private:
    TrieNode* root;
public:
   Trie() {
      root = new TrieNode();
   }
   void insert(std::string word) {
      TrieNode* curr = root;
      for (char ch : word) {
         if (curr->children.find(ch) == curr->children.end()) {
            curr->children[ch] = new TrieNode();
         }
         curr = curr->children[ch];
      }
      curr->isEndOfWord = true;
   }
   TrieNode* getRoot() {
       return root;
   }
};

void printWords(TrieNode* node, std::string prefix) {
   if (node->isEndOfWord) {
       std::cout << prefix << std::endl;
   }
   for (auto entry : node->children) {
       printWords(entry.second, prefix + entry.first);
   }
}
int main() {
   Trie car;
   car.insert("Lamborghini");
   car.insert("Mercedes-Benz");
   car.insert("Land Rover");
   car.insert("Maruti Suzuki");
   std::cout << "Tries elements are: " << std::endl;
   printWords(car.getRoot(), "");
   return 0;
}

Output

Tries elements are: 
Maruti Suzuki
Mercedes-Benz
Land Rover
Lamborghini

import java.util.HashMap;
import java.util.Map;
class TrieNode {
   Map<Character, TrieNode> children;
   boolean isEndOfWord;
   TrieNode() {
       children = new HashMap<>();
       isEndOfWord = false;
   }
}
class Trie {
   private TrieNode root;
   Trie() {
      root = new TrieNode();
   }
   
   void insert(String word) {
      TrieNode curr = root;
      for (char ch : word.toCharArray()) {
          curr.children.putIfAbsent(ch, new TrieNode());
          curr = curr.children.get(ch);
      }
      curr.isEndOfWord = true;
   }
   TrieNode getRoot() {
      return root;
   }
}
public class Main {
   public static void printWords(TrieNode node, String prefix) {
      if (node.isEndOfWord) {
         System.out.println(prefix);
      }
      
      for (Map.Entry<Character, TrieNode> entry : node.children.entrySet()) {
         printWords(entry.getValue(), prefix + entry.getKey());
      }
   }
   public static void main(String[] args) {
      Trie car = new Trie();
      // Inserting the elements
      car.insert("Lamborghini");
      car.insert("Mercedes-Benz");
      car.insert("Land Rover");
      car.insert("Maruti Suzuki");
      // Print the inserted objects
      System.out.print("Tries elements are: \n");
      printWords(car.getRoot(), ""); // Access root using the public method
   }
}

Output

Tries elements are: 
Lamborghini
Land Rover
Maruti Suzuki
Mercedes-Benz

class TrieNode:
    def __init__(self):
        self.children = {}
        self.isEndOfWord = False
class Trie:
    def __init__(self):
        self.root = TrieNode()
    def insert(self, word):
        curr = self.root
        for ch in word:
            curr.children.setdefault(ch, TrieNode())
            curr = curr.children[ch]
        curr.isEndOfWord = True
    def getRoot(self):
        return self.root
def printWords(node, prefix):
    if node.isEndOfWord:
        print(prefix)
    for ch, child in node.children.items():
        printWords(child, prefix + ch)

if __name__ == '__main__':
    car = Trie()
    # Inserting the elements
    car.insert("Lamborghini")
    car.insert("Mercedes-Benz")
    car.insert("Land Rover")
    car.insert("Maruti Suzuki")
    # Print the inserted objects
    print("Tries elements are: ")
    printWords(car.getRoot(), "")

Output

Tries elements are: 
Lamborghini
Land Rover
Mercedes-Benz
Maruti Suzuki

Deletion operation

The deletion operation in a trie is performed using the bottom-up approach. The element is searched for in a trie and deleted, if found. However, there are some special scenarios that need to be kept in mind while performing the deletion operation.

Case 1 − The key is unique − in this case, the entire key path is deleted from the node. (Unique key suggests that there is no other path that branches out from one path).

Case 2 − The key is not unique − the leaf nodes are updated. For example, if the key to be deleted is see but it is a prefix of another key seethe; we delete the see and change the Boolean values of t, h and e as false.

Case 3 − The key to be deleted already has a prefix − the values until the prefix are deleted and the prefix remains in the tree. For example, if the key to be deleted is heart but there is another key present he; so we delete a, r, and t until only he remains.

Example

Following are the implementations of this operation in various programming languages −

C C++ Java Python 
//C code for Deletion Operation of tries Algorithm
#include <stdio.h>
#include <stdlib.h>
#include <stdbool.h>
#include <string.h>
//Define size 26
#define ALPHABET_SIZE 26
struct TrieNode {
   struct TrieNode* children[ALPHABET_SIZE];
   bool isEndOfWord;
};
struct Trie {
    struct TrieNode* root;
};
struct TrieNode* createNode() {
   struct TrieNode* node = (struct TrieNode*)malloc(sizeof(struct TrieNode));
   node->isEndOfWord = false;
   for (int i = 0; i < ALPHABET_SIZE; i++) {
      node->children[i] = NULL;
   }
   return node;
}
void insert(struct Trie* trie, const char* key) {
    struct TrieNode* curr = trie->root;
    for (int i = 0; i < strlen(key); i++) {
        int index = key[i] - 'a';
        if (curr->children[index] == NULL) {
            curr->children[index] = createNode();
        }
        curr = curr->children[index];
    }
    curr->isEndOfWord = 1;
}
bool search(struct TrieNode* root, char* word) {
   struct TrieNode* curr = root;
   for (int i = 0; word[i] != '\0'; i++) {
      int index = word[i] - 'a';
      if (curr->children[index] == NULL) {
         return false;
      }
      curr = curr->children[index];
   }
   return (curr != NULL && curr->isEndOfWord);
}
bool startsWith(struct TrieNode* root, char* prefix) {
   struct TrieNode* curr = root;
   for (int i = 0; prefix[i] != '\0'; i++) {
      int index = prefix[i] - 'a';
      if (curr->children[index] == NULL) {
         return false;
      }
      curr = curr->children[index];
   }
   return true;
}
bool deleteWord(struct TrieNode* root, char* word) {
   struct TrieNode* curr = root;
   struct TrieNode* parent = NULL;
   int index;
   for (int i = 0; word[i] != '\0'; i++) {
      index = word[i] - 'a';
      if (curr->children[index] == NULL) {
          return false; // Word does not exist in the Trie
      }
      parent = curr;
      curr = curr->children[index];
   }
   if (!curr->isEndOfWord) {
      return false; // Word does not exist in the Trie
   }
   curr->isEndOfWord = false; // Mark as deleted
   if (parent != NULL) {
      parent->children[index] = NULL; // Remove the child node
   }
   return true;
}
void printWords(struct TrieNode* node, char* prefix) {
    if (node->isEndOfWord) {
        printf("%s\n", prefix);
    }
    for (int i = 0; i < ALPHABET_SIZE; i++) {
        if (node->children[i] != NULL) {
            char* newPrefix = (char*)malloc(strlen(prefix) + 2);
            strcpy(newPrefix, prefix);
            newPrefix[strlen(prefix)] = 'a' + i;
            newPrefix[strlen(prefix) + 1] = '\0';
            printWords(node->children[i], newPrefix);
            free(newPrefix);
        }
    }
}
int main() {
    struct Trie car;
    car.root = createNode();
    insert(&car, "lamborghini");
    insert(&car, "mercedes-Benz");
    insert(&car, "landrover");
    insert(&car, "maruti Suzuki");
   //Before Deletion
   printf("Tries elements before deletion: \n");
   printWords(car.root, "");
   //Deleting the elements
   char* s1  = "lamborghini";
   char* s2 = "landrover";
   printf("Elements to be deleted are: %s and %s", s1, s2);
   deleteWord(car.root, s1);
   deleteWord(car.root, s2);
   //After Deletion
   printf("\nTries elements before deletion: \n");
   printWords(car.root, "");
}

Output

Tries elements before deletion: 
lamborghini
landrover
marutiouzuki
mercezenz
Elements to be deleted are: lamborghini and landrover
Tries elements before deletion: 
marutiouzuki
mercezenz

//C++ code for Deletion operation of tries algorithm
#include <iostream>
#include <unordered_map>
using namespace std;
class TrieNode {
public:
   unordered_map<char, TrieNode*> children;
   bool isEndOfWord;
   TrieNode() {
      isEndOfWord = false;
   }
};
class Trie {
private:
   TrieNode* root;
public:
   Trie() {
      root = new TrieNode();
   }
   void insert(string word) {
      TrieNode* curr = root;
      for (char ch : word) {
         if (curr->children.find(ch) == curr->children.end()) {
            curr->children[ch] = new TrieNode();
         }
         curr = curr->children[ch];
      }
      curr->isEndOfWord = true;
   }
TrieNode* getRoot() {
       return root;
    }
    bool deleteWord(string word) {
       return deleteHelper(root, word, 0);
    }
private:
   bool deleteHelper(TrieNode* curr, string word, int index) {
      if (index == word.length()) {
         if (!curr->isEndOfWord) {
             return false; // Word does not exist in the Trie
         }
         curr->isEndOfWord = false; // Mark as deleted
         return curr->children.empty(); // Return true if no more children
      }
      char ch = word[index];
      if (curr->children.find(ch) == curr->children.end()) {
         return false; // Word does not exist in the Trie
      }
      TrieNode* child = curr->children[ch];
      bool shouldDeleteChild = deleteHelper(child, word, index + 1);
      
      if (shouldDeleteChild) {
         curr->children.erase(ch); // Remove the child node if necessary
         return curr->children.empty(); // Return true if no more children
      }
      return false;
   }
};
void printWords(TrieNode* node, std::string prefix) {
   if (node->isEndOfWord) {
      std::cout << prefix << std::endl;
   }
   for (auto entry : node->children) {
      printWords(entry.second, prefix + entry.first);
   }
}
int main() {
   Trie car;
   //inserting the elemnets
   car.insert("Lamborghini");
   car.insert("Mercedes-Benz");
   car.insert("Land Rover");
   car.insert("Maruti Suzuki");
   //Before Deletion
   cout <<"Tries elements before deletion: \n";
   printWords(car.getRoot(), "");
   //Deleting elements using deletion operation
   string s1 = "Lamborghini";
   string s2 = "Land Rover";
   cout<<"Elements to be deleted are: \n"<<s1<<" and "<<s2;
   car.deleteWord("Lamborghini");
   car.deleteWord("Land Rover");
   //After Deletion
   cout << "\nTries elements after deletion: \n";
   printWords(car.getRoot(), "");
}

Output

Tries elements before deletion: 
Maruti Suzuki
Mercedes-Benz
Land Rover
Lamborghini
Elements to be deleted are: 
Lamborghini and Land Rover
Tries elements after deletion: 
Maruti Suzuki
Mercedes-Benz

//Java code for Deletion operator of tries algotrithm
import java.util.HashMap;
import java.util.Map;
class TrieNode {
   Map<Character, TrieNode> children;
   boolean isEndOfWord;
   
   TrieNode() {
      children = new HashMap<>();
      isEndOfWord = false;
   }
}
class Trie {
   private TrieNode root;
   Trie() {
      root = new TrieNode();
   }
   void insert(String word) {
      TrieNode curr = root;
      for (char ch : word.toCharArray()) {
         curr.children.putIfAbsent(ch, new TrieNode());
         curr = curr.children.get(ch);
      }
      curr.isEndOfWord = true;
   }
   TrieNode getRoot() {
      return root;
   }
   boolean delete(String word) {
      return deleteHelper(root, word, 0);
   }
   private boolean deleteHelper(TrieNode curr, String word, int index) {
      if (index == word.length()) {
         if (!curr.isEndOfWord) {
             return false; // Word does not exist in the Trie
         }
         curr.isEndOfWord = false; // Mark as deleted
         return curr.children.isEmpty(); // Return true if no more children
      }
      char ch = word.charAt(index);
      if (!curr.children.containsKey(ch)) {
         return false; // Word does not exist in the Trie
      }
      TrieNode child = curr.children.get(ch);
      boolean shouldDeleteChild = deleteHelper(child, word, index + 1);
      if (shouldDeleteChild) {
         curr.children.remove(ch); // Remove the child node if necessary
         return curr.children.isEmpty(); // Return true if no more children
      }
      
      return false;
   }
}
public class Main {
   public static void printWords(TrieNode node, String prefix) {
      if (node.isEndOfWord) {
          System.out.println(prefix);
      }
      
      for (Map.Entry<Character, TrieNode> entry : node.children.entrySet()) {
          printWords(entry.getValue(), prefix + entry.getKey());
      }
   }
   public static void main(String[] args) {
      Trie car = new Trie(); 
      //Inserting the elements
      car.insert("Lamborghini");
      car.insert("Mercedes-Benz");
      car.insert("Land Rover");
      car.insert("Maruti Suzuki");
      //Before Deletion
      System.out.println("Tries elements before deletion: ");
      printWords(car.getRoot(), "");
      String s1 = "Lamborghini";
      String s2 = "Land Rover";
      System.out.print("Element to be deleted are: \n" + s1 + " and " + s2);
      car.delete(s1);
      car.delete(s2);
      System.out.println("\nTries elements after deletion: ");
      printWords(car.getRoot(), "");
   }
}

Output

Tries elements before deletion: 
Lamborghini
Land Rover
Maruti Suzuki
Mercedes-Benz
Element to be deleted are: 
Lamborghini and Land Rover
Tries elements after deletion: 
Maruti Suzuki
Mercedes-Benz

#python Code for Deletion operation of tries algorithm
class TrieNode:
    def __init__(self):
        self.children = {}
        self.isEndOfWord = False
class Trie:
    def __init__(self):
        self.root = TrieNode()
    def insert(self, word):
        curr = self.root
        for ch in word:
            if ch not in curr.children:
                curr.children[ch] = TrieNode()
            curr = curr.children[ch]
        curr.isEndOfWord = True
    def search(self, word):
        curr = self.root
        for ch in word:
            if ch not in curr.children:
                return False
            curr = curr.children[ch]
        return curr.isEndOfWord
    def startsWith(self, prefix):
        curr = self.root
        for ch in prefix:
            if ch not in curr.children:
                return False
            curr = curr.children[ch]
        return True
    def delete(self, word):
        return self.deleteHelper(self.root, word, 0)

    def deleteHelper(self, curr, word, index):
        if index == len(word):
            if not curr.isEndOfWord:
                return False  # Word does not exist in the Trie
            curr.isEndOfWord = False  # Mark as deleted
            return len(curr.children) == 0  # Return True if no more children
        ch = word[index]
        if ch not in curr.children:
            return False  # Word does not exist in the Trie
        child = curr.children[ch]
        shouldDeleteChild = self.deleteHelper(child, word, index + 1)
        if shouldDeleteChild:
            del curr.children[ch]  # Remove the child node if necessary
            return len(curr.children) == 0  # Return True if no more children
        return False
    def getRoot(self):
        return self.root
def printWords(node, prefix):
    if node.isEndOfWord:
        print(prefix)
    for ch, child in node.children.items():
        printWords(child, prefix + ch)
trie = Trie()
#inserting the elements
trie.insert("Lamborghini")
trie.insert("Mercedes-Benz")
trie.insert("Land Rover")
trie.insert("Maruti Suzuki")
#Before Deletion
print("Tries elements before deletion: ")
printWords(trie.getRoot(), "")
#deleting the elements using Deletion operation
s1 = "Lamborghini"
s2 = "Land Rover"
print("Elements to be deleted are:\n",s1 ,"and",s2)
trie.delete(s1)
trie.delete(s2)
print("Tries elements after deletion: ")
printWords(trie.getRoot(), "")

Output

Tries elements before deletion: 
Lamborghini
Land Rover
Mercedes-Benz
Maruti Suzuki
Elements to be deleted are:
 Lamborghini and Land Rover
Tries elements after deletion: 
Mercedes-Benz
Maruti Suzuki

Searching in a trie is a rather straightforward approach. We can only move down the levels of trie based on the key node (the nodes where insertion operation starts at). Searching is done until the end of the path is reached. If the element is found, search is successful; otherwise, search is prompted unsuccessful.

Example

Following are the implementations of this operation in various programming languages −

C C++ Java Python 
//C program for search operation of tries algorithm
#include <stdio.h>
#include <stdlib.h>
#include <stdbool.h>
#define ALPHABET_SIZE 26
struct TrieNode {
   struct TrieNode* children[ALPHABET_SIZE];
   bool isEndOfWord;
};
struct TrieNode* createNode() {
   struct TrieNode* node = (struct TrieNode*)malloc(sizeof(struct TrieNode));
   node->isEndOfWord = false;
   
   for (int i = 0; i < ALPHABET_SIZE; i++) {
      node->children[i] = NULL;
   }
   return node;
}

void insert(struct TrieNode* root, char* word) {
   struct TrieNode* curr = root;
   for (int i = 0; word[i] != '\0'; i++) {
      int index = word[i] - 'a';    
      if (curr->children[index] == NULL) {
         curr->children[index] = createNode();
      }  
      curr = curr->children[index];
   } 
   curr->isEndOfWord = true;
}
bool search(struct TrieNode* root, char* word) {
   struct TrieNode* curr = root;   
   for (int i = 0; word[i] != '\0'; i++) {
      int index = word[i] - 'a';
      if (curr->children[index] == NULL) {
         return false;
      }   
      curr = curr->children[index];
   }
   return (curr != NULL && curr->isEndOfWord);
}
bool startsWith(struct TrieNode* root, char* prefix) {
   struct TrieNode* curr = root;
   for (int i = 0; prefix[i] != '\0'; i++) {
      int index = prefix[i] - 'a';  
      if (curr->children[index] == NULL) {
         return false;
      } 
      curr = curr->children[index];
   }
   return true;
}

int main() {
   struct TrieNode* root = createNode();
   //inserting the elements
   insert(root, "Lamborghini");
   insert(root, "Mercedes-Benz");
   insert(root, "Land Rover");
   insert(root, "Maruti Suzuki");    
   //Searching elements
   printf("Searching Cars\n");
   //Printing searched elements
   printf("Found? %d\n", search(root, "Lamborghini"));     // Output: 1 (true)
   printf("Found? %d\n", search(root, "Mercedes-Benz"));   // Output: 1 (true)
   printf("Found? %d\n", search(root, "Honda"));           // Output: 0 (false)
   printf("Found? %d\n", search(root, "Land Rover"));      // Output: 1 (true)
   printf("Found? %d\n", search(root, "BMW"));             // Output: 0 (false)   
   //Searching the elements the name starts with?
   printf("Cars name starts with\n");
   //Printing the elements
   printf("Does car name starts with 'Lambo'? %d\n", startsWith(root, "Lambo"));       // Output: 1 (true)
   printf("Does car name starts with 'Hon'? %d\n", startsWith(root, "Hon"));         // Output: 0 (false)
   printf("Does car name starts with 'Hy'? %d\n", startsWith(root, "Hy"));          // Output: 0 (false)
   printf("Does car name starts with 'Mar'? %d\n", startsWith(root, "Mar"));         // Output: 1 (true)
   printf("Does car name starts with 'Land'? %d\n", startsWith(root, "Land"));        // Output: 1 (true)   
   return 0;
}

Output

Searching Cars
Found? 1
Found? 1
Found? 0
Found? 1
Found? 0
Cars name starts with
Does car name starts with 'Lambo'? 1
Does car name starts with 'Hon'? 0
Does car name starts with 'Hy'? 0
Does car name starts with 'Mar'? 1
Does car name starts with 'Land'? 1

//C++ code for Search operation of tries algorithm
#include <iostream>
#include <unordered_map>
using namespace std;
class TrieNode {
public:
   unordered_map<char, TrieNode*> children;
   bool isEndOfWord;
   
   TrieNode() {
      isEndOfWord = false;
   }
};
class Trie {
private:
    TrieNode* root;
public:
   Trie() {
      root = new TrieNode();
   }
   void insert(string word) {
      TrieNode* curr = root;
      for (char ch : word) {
         if (curr->children.find(ch) == curr->children.end()) {
            curr->children[ch] = new TrieNode();
         }
         curr = curr->children[ch];
      }
      curr->isEndOfWord = true;
   }
   TrieNode* getRoot() {
      return root;
   }
   bool search(string word) {
      TrieNode* curr = root;
      for (char ch : word) {
         if (curr->children.find(ch) == curr->children.end()) {
            return false;
         }
         curr = curr->children[ch];
      }
      return curr->isEndOfWord;
   }
   bool startsWith(string prefix) {
      TrieNode* curr = root;
      for (char ch : prefix) {
         if (curr->children.find(ch) == curr->children.end()) {
            return false;
         }
         curr = curr->children[ch];
      }
      return true;
   }
};
void printWords(TrieNode* node, std::string prefix) {
   if (node->isEndOfWord) {
      std::cout << prefix << std::endl;
   }
   for (auto entry : node->children) {
      printWords(entry.second, prefix + entry.first);
   }
}
int main() {
   Trie car;
   //inserting the elements
   car.insert("Lamborghini");
   car.insert("Mercedes-Benz");
   car.insert("Land Rover");
   car.insert("Maruti Suzuki");
   cout<<"Tries elements are: "<<endl;
   printWords(car.getRoot(), "");
   //searching elements
   cout<<"Searching Cars"<< endl; 
   // Printing searched elements in Boolean expression
   cout << "Found? "<<car.search("Lamborghini") << endl;     // Output: 1 (true)
   cout << "Found? "<<car.search("Mercedes-Benz") << endl;    // Output: 1 (true)
   cout << "Found? "<<car.search("Honda") << endl;     // Output: 0 (false)
   cout << "Found? "<<car.search("Land Rover") << endl;    // Output: 1 (true)
   cout << "Found? "<<car.search("BMW") << endl;   // Output: 0 (false)   
   //searching names starts with?
   cout<<"Cars name starts with" << endl;
   //Printing the elements
   cout << "Does car name starts with 'Lambo'? "<<car.startsWith("Lambo") << endl;   // Output: 1 (true)
   cout << "Does car name starts with 'Hon'? "<< car.startsWith("Hon") << endl;    // Output: 0 (false)
   cout << "Does car name starts with 'Hy'? "<< car.startsWith("Hy") << endl;    // Output: 0 (false)
   cout << "Does car name starts with 'Mer'? "<< car.startsWith("Mar") << endl;    // Output: 1 (true)
   cout << "Does car name starts with 'Land'? "<< car.startsWith("Land")<< endl;   // Output: 1 (true)
   return 0;
}

Output

Tries elements are: 
Maruti Suzuki
Mercedes-Benz
Land Rover
Lamborghini
Searching Cars
Found? 1
Found? 1
Found? 0
Found? 1
Found? 0
Cars name starts with
Does car name starts with 'Lambo'? 1
Does car name starts with 'Hon'? 0
Does car name starts with 'Hy'? 0
Does car name starts with 'Mer'? 1
Does car name starts with 'Land'? 1

//Java program for tries Algorithm
import java.util.HashMap;
import java.util.Map;
class TrieNode {
   Map<Character, TrieNode> children;
   boolean isEndOfWord;
   TrieNode() {
      children = new HashMap<>();
      isEndOfWord = false;
   }
}
class Trie {
   private TrieNode root;
   Trie() {
      root = new TrieNode();
   }
   void insert(String word) {
      TrieNode curr = root;
      for (char ch : word.toCharArray()) {
         curr.children.putIfAbsent(ch, new TrieNode());
         curr = curr.children.get(ch);
      }
      curr.isEndOfWord = true;
   }
TrieNode getRoot() {
   return root;
   }
   boolean search(String word) {
      TrieNode curr = root;
      for (char ch : word.toCharArray()) {
         if (!curr.children.containsKey(ch)) {
            return false;
         }
         curr = curr.children.get(ch);
      }
      return curr.isEndOfWord;
   }
   boolean startsWith(String prefix) {
      TrieNode curr = root;
      for (char ch : prefix.toCharArray()) {
         if (!curr.children.containsKey(ch)) {
            return false;
         }
         curr = curr.children.get(ch);
      }
      return true;
   }
}
public class Main {
public static void printWords(TrieNode node, String prefix) {
   if (node.isEndOfWord) {
      System.out.println(prefix);
   }
   for (Map.Entry<Character, TrieNode> entry : node.children.entrySet()) {
      printWords(entry.getValue(), prefix + entry.getKey());
   }
}
   public static void main(String[] args) {
      Trie car = new Trie();
      //Inserting the elements
      car.insert("Lamborghini");
      car.insert("Mercedes-Benz");
      car.insert("Land Rover");
      car.insert("Maruti Suzuki");
      System.out.print("Tries elements are: \n");
      printWords(car.getRoot(), " ");
      //searching the elements
      System.out.println("Searching Cars");
      //Printing the searched elements
      System.out.println("Found? " + car.search("Lamborghini"));     // Output: true
      System.out.println("Found? " + car.search("Mercedes-Benz"));   // Output: true
      System.out.println("Found? " + car.search("Honda"));           // Output: false
      System.out.println("Found? " + car.search("Land Rover"));      // Output: true
      System.out.println("Found? " + car.search("BMW"));             // Output: false  
      //searching the elements name start with?
      System.out.println("Cars name starts with");
      //Printing the elements
      System.out.println("Does car name starts with 'Lambo'? " + car.startsWith("Lambo"));       // Output: true
      System.out.println("Does car name starts with 'Hon'? " + car.startsWith("Hon"));         // Output: false
      System.out.println("Does car name starts with 'Hy'? " + car.startsWith("Hy"));          // Output: false
      System.out.println("Does car name starts with 'Mer'? " +car.startsWith("Mar"));         // Output: true
      System.out.println("Does car name starts with 'Land'? " + car.startsWith("Land"));        // Output: true
   }
}

Output

Tries elements are: 
 Lamborghini
 Land Rover
 Maruti Suzuki
 Mercedes-Benz
Searching Cars
Found? true
Found? true
Found? false
Found? true
Found? false
Cars name starts with
Does car name starts with 'Lambo'? true
Does car name starts with 'Hon'? false
Does car name starts with 'Hy'? false
Does car name starts with 'Mer'? true
Does car name starts with 'Land'? true

#Python code for Search operation of tries algorithm
class TrieNode:
    def __init__(self):
        self.children = {}
        self.isEndOfWord = False
class Trie:
    def __init__(self):
        self.root = TrieNode()
    def insert(self, word):
        curr = self.root
        for ch in word:
            if ch not in curr.children:
                curr.children[ch] = TrieNode()
            curr = curr.children[ch]
        curr.isEndOfWord = True
    def search(self, word):
        curr = self.root
        for ch in word:
            if ch not in curr.children:
                return False
            curr = curr.children[ch]
        return curr.isEndOfWord
    def startsWith(self, prefix):
        curr = self.root
        for ch in prefix:
            if ch not in curr.children:
                return False
            curr = curr.children[ch]
        return True
    def getRoot(self):
        return self.root
def printWords(node, prefix):
    if node.isEndOfWord:
        print(prefix)
    for ch, child in node.children.items():
        printWords(child, prefix + ch)
if __name__ == '__main__':
    car = Trie()
   #Inserting the elements
    car.insert("Lamborghini")
    car.insert("Mercedes-Benz")
    car.insert("Land Rover")
    car.insert("Maruti Suzuki")
    print("Tries elements are: ")
    printWords(car.root, " ")
    #Searching elements
    print("Searching Cars")
    #Printing the searched elements
    print("Found?",car.search("Lamborghini"))     # Output: True
    print("Found?",car.search("Mercedes-Benz"))   # Output: True
    print("Found?",car.search("Honda"))           # Output: False
    print("Found?",car.search("Land Rover"))      # Output: True
    print("Found?",car.search("BMW"))             # Output: False
    #printing elements name starts with?
    print("Cars name starts with")
    print("Does car name starts with 'Lambo'?", car.startsWith("Lambo"))       # Output: True
    print("Does car name starts with 'Hon'?",car.startsWith("Hon"))         # Output: False
    print("Does car name starts with 'Hy'?",car.startsWith("Hy"))          # Output: False
    print("Does car name starts with 'Mer'?",car.startsWith("Mer"))         # Output: True
    print("Does car name starts with 'Land'?",car.startsWith("Land"))        # Output: True

Output

Tries elements are: 
 Lamborghini
 Land Rover
 Mercedes-Benz
 Maruti Suzuki
Searching Cars
Found? True
Found? True
Found? False
Found? True
Found? False
Cars name starts with
Does car name starts with 'Lambo'? True
Does car name starts with 'Hon'? False
Does car name starts with 'Hy'? False
Does car name starts with 'Mer'? True
Does car name starts with 'Land'? True
Print Page
Previous
Next
Advertisements