
- Data Structures & Algorithms
- DSA - Home
- DSA - Overview
- DSA - Environment Setup
- DSA - Algorithms Basics
- DSA - Asymptotic Analysis
- Data Structures
- DSA - Data Structure Basics
- DSA - Data Structures and Types
- DSA - Array Data Structure
- Linked Lists
- DSA - Linked List Data Structure
- DSA - Doubly Linked List Data Structure
- DSA - Circular Linked List Data Structure
- Stack & Queue
- DSA - Stack Data Structure
- DSA - Expression Parsing
- DSA - Queue Data Structure
- Searching Algorithms
- DSA - Searching Algorithms
- DSA - Linear Search Algorithm
- DSA - Binary Search Algorithm
- DSA - Interpolation Search
- DSA - Jump Search Algorithm
- DSA - Exponential Search
- DSA - Fibonacci Search
- DSA - Sublist Search
- DSA - Hash Table
- Sorting Algorithms
- DSA - Sorting Algorithms
- DSA - Bubble Sort Algorithm
- DSA - Insertion Sort Algorithm
- DSA - Selection Sort Algorithm
- DSA - Merge Sort Algorithm
- DSA - Shell Sort Algorithm
- DSA - Heap Sort
- DSA - Bucket Sort Algorithm
- DSA - Counting Sort Algorithm
- DSA - Radix Sort Algorithm
- DSA - Quick Sort Algorithm
- Graph Data Structure
- DSA - Graph Data Structure
- DSA - Depth First Traversal
- DSA - Breadth First Traversal
- DSA - Spanning Tree
- Tree Data Structure
- DSA - Tree Data Structure
- DSA - Tree Traversal
- DSA - Binary Search Tree
- DSA - AVL Tree
- DSA - Red Black Trees
- DSA - B Trees
- DSA - B+ Trees
- DSA - Splay Trees
- DSA - Tries
- DSA - Heap Data Structure
- Recursion
- DSA - Recursion Algorithms
- DSA - Tower of Hanoi Using Recursion
- DSA - Fibonacci Series Using Recursion
- Divide and Conquer
- DSA - Divide and Conquer
- DSA - Max-Min Problem
- DSA - Strassen's Matrix Multiplication
- DSA - Karatsuba Algorithm
- Greedy Algorithms
- DSA - Greedy Algorithms
- DSA - Travelling Salesman Problem (Greedy Approach)
- DSA - Prim's Minimal Spanning Tree
- DSA - Kruskal's Minimal Spanning Tree
- DSA - Dijkstra's Shortest Path Algorithm
- DSA - Map Colouring Algorithm
- DSA - Fractional Knapsack Problem
- DSA - Job Sequencing with Deadline
- DSA - Optimal Merge Pattern Algorithm
- Dynamic Programming
- DSA - Dynamic Programming
- DSA - Matrix Chain Multiplication
- DSA - Floyd Warshall Algorithm
- DSA - 0-1 Knapsack Problem
- DSA - Longest Common Subsequence Algorithm
- DSA - Travelling Salesman Problem (Dynamic Approach)
- Approximation Algorithms
- DSA - Approximation Algorithms
- DSA - Vertex Cover Algorithm
- DSA - Set Cover Problem
- DSA - Travelling Salesman Problem (Approximation Approach)
- Randomized Algorithms
- DSA - Randomized Algorithms
- DSA - Randomized Quick Sort Algorithm
- DSA - Karger’s Minimum Cut Algorithm
- DSA - Fisher-Yates Shuffle Algorithm
- DSA Useful Resources
- DSA - Questions and Answers
- DSA - Quick Guide
- DSA - Useful Resources
- DSA - Discussion
Divide & Conquer Algorithm
Using divide and conquer approach, the problem in hand, is divided into smaller sub-problems and then each problem is solved independently. When we keep dividing the sub-problems into even smaller sub-problems, we may eventually reach a stage where no more division is possible. Those smallest possible sub-problems are solved using original solution because it takes lesser time to compute. The solution of all sub-problems is finally merged in order to obtain the solution of the original problem.
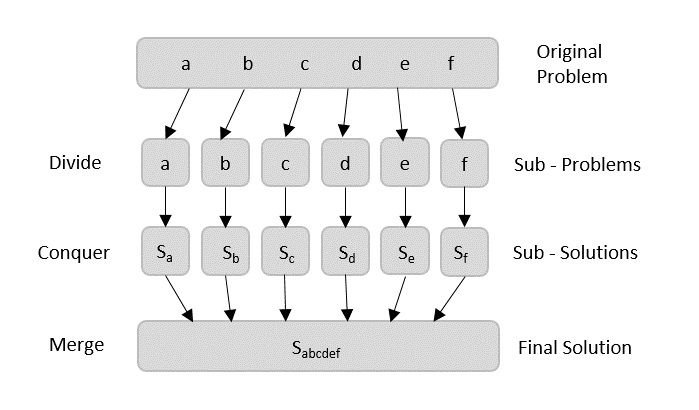
Broadly, we can understand divide-and-conquer approach in a three-step process.
Divide/Break
This step involves breaking the problem into smaller sub-problems. Sub-problems should represent a part of the original problem. This step generally takes a recursive approach to divide the problem until no sub-problem is further divisible. At this stage, sub-problems become atomic in size but still represent some part of the actual problem.
Conquer/Solve
This step receives a lot of smaller sub-problems to be solved. Generally, at this level, the problems are considered 'solved' on their own.
Merge/Combine
When the smaller sub-problems are solved, this stage recursively combines them until they formulate a solution of the original problem. This algorithmic approach works recursively and conquer & merge steps works so close that they appear as one.
Arrays as Input
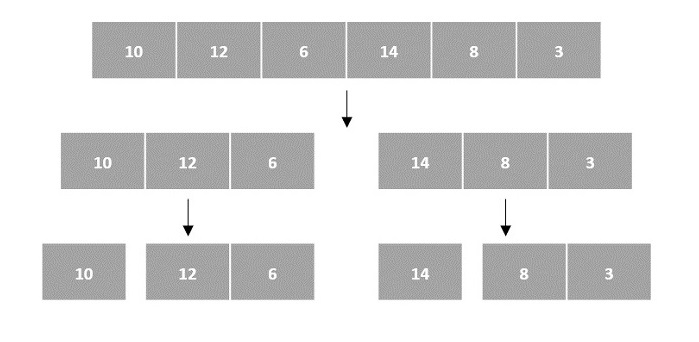
There are various ways in which various algorithms can take input such that they can be solved using the divide and conquer technique. Arrays are one of them. In algorithms that require input to be in the form of a list, like various sorting algorithms, array data structures are most commonly used.
In the input for a sorting algorithm below, the array input is divided into subproblems until they cannot be divided further.
Then, the subproblems are sorted (the conquer step) and are merged to form the solution of the original array back (the combine step).
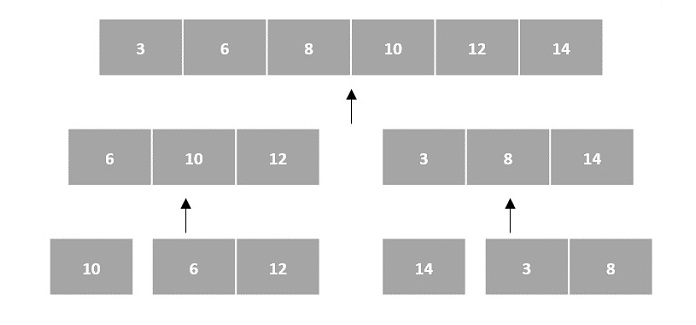
Since arrays are indexed and linear data structures, sorting algorithms most popularly use array data structures to receive input.
Linked Lists as Input
Another data structure that can be used to take input for divide and conquer algorithms is a linked list (for example, merge sort using linked lists). Like arrays, linked lists are also linear data structures that store data sequentially.
Consider the merge sort algorithm on linked list; following the very popular tortoise and hare algorithm, the list is divided until it cannot be divided further.
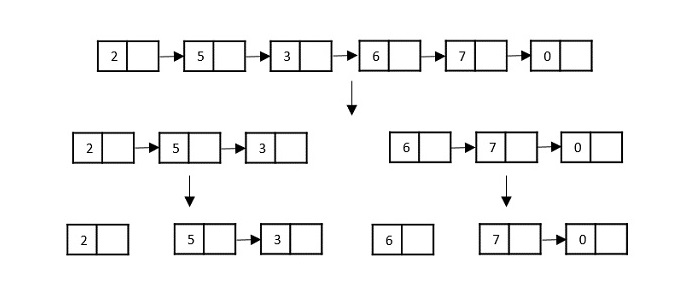
Then, the nodes in the list are sorted (conquered). These nodes are then combined (or merged) in recursively until the final solution is achieved.
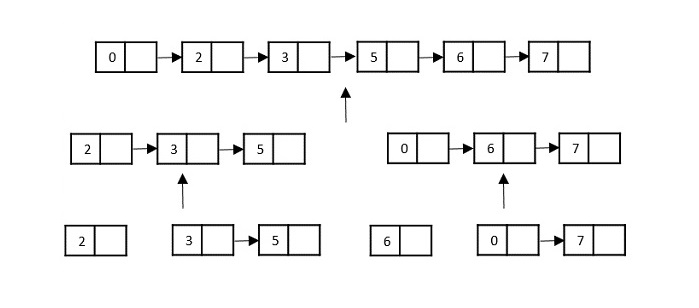
Various searching algorithms can also be performed on the linked list data structures with a slightly different technique as linked lists are not indexed linear data structures. They must be handled using the pointers available in the nodes of the list.
Pros and cons of Divide and Conquer Approach
Divide and conquer approach supports parallelism as sub-problems are independent. Hence, an algorithm, which is designed using this technique, can run on the multiprocessor system or in different machines simultaneously.
In this approach, most of the algorithms are designed using recursion, hence memory management is very high. For recursive function stack is used, where function state needs to be stored.
Examples of Divide and Conquer Approach
The following computer algorithms are based on divide-and-conquer programming approach −
Closest pair (points)
There are various ways available to solve any computer problem, but the mentioned are a good example of divide and conquer approach.
