Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
What is Ambiguous Grammar?
A Grammar that makes more than one Leftmost Derivation (or Rightmost Derivation) for the similar sentence is called Ambiguous Grammar.
Example − Verify whether the following Grammar is Ambiguous or Not.
E → E+E|E $\ast$ E|id
Solution
For string id + id * id, there exist two parse trees.
E ⇒lm $\underline{E}$+E
⇒ id+ $\underline{E}$
⇒ id+$\underline{E}$ $\ast$ E
⇒ id+id $\ast$ $\underline{E}$
⇒ id+id $\ast$ id
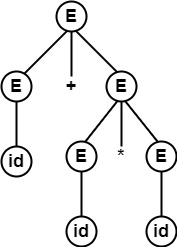
E ⇒lm $\underline{E}$ $\ast$ E
⇒ $\underline{E}$+E $\ast$ E
⇒ id+ $\underline{E}$ $\ast$ E
⇒ id+id $\ast$ $\underline{E}$
⇒ id+id $\ast$ id
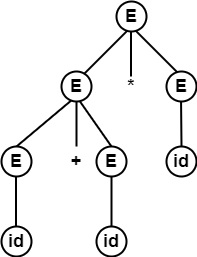
So, the same string is generated using two different leftmost derivations. Each is having a different parse tree.
∴ Two different parse trees exist for string id + id * id.
∴ Grammar is Ambiguous.
Conversion of Ambiguous to Unambiguous Grammar
The productions containing more than one occurrence of a given non-terminal on its right-hand side are ambiguous productions.
Example − E → $\underline{E}$ * $\underline{E}$
It contains two E’s on R.H.S.
It can convert these types of Ambiguous productions to Unambiguous production by introducing a new Non-terminal to move right most of these non-terminal farther down the Parse Tree.
Example1 − Consider the Grammar
E → E+E|E $\ast$ E|(E)| id
Convert this Ambiguous Grammar into Unambiguous Grammar.
Solution
Step1 − Introduction a non-terminal T (term) which cannot be further addition of two terms.
E → E+T | T T → E * E | (E) |id
Step2 − As we have production E → T. Substitute E with T to get
T→T∗T
Introduce another non-terminal F (factor) that cannot be further factorized or cannot be multiplication of two numbers.
Substitute T with F to get,
T → T * F | F F → (E) | id
∴ Unambiguous Grammar will be
E → E+T | T T → T * F | F F → (E) | id
Example2 − Prove that following Grammar is Ambiguous for the string if c then if c2 then s1 else s2.
<statement> →if<cond> then<statement> | if<cond> then<statement> else<statement>
| another statement
Convert it into Unambiguous Grammar.
Solution
Given grammar is Ambiguous since there exists two Parse Trees for the same string because else condition can belong to any if statement.
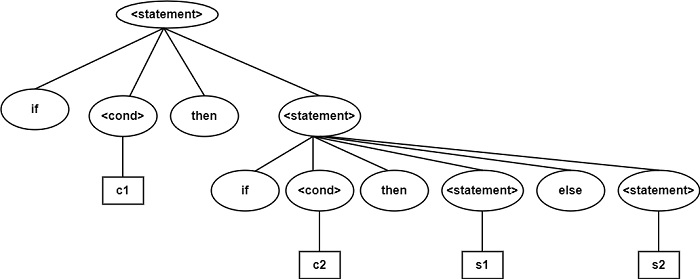
In the above Parse tree, else belongs to second if.
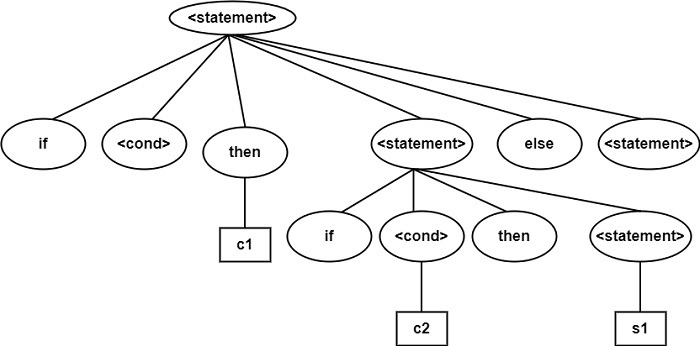
In the above Parse tree, else belongs to first if.
Conversion to Unambiguous Grammar
The Unambiguous Grammar will be −
<statement>→<match−statement>|<Unmatch−statement> <match−statement>→if<cond>then<match−statement>else <match−statement>| other−statement <Unmatch−statement>→if<cond>then<statement>| if<cond>then <match−statement>else<Unmatch Statement>
14K+ Views
