How to convert left linear grammar to right linear grammar?

Regular grammar describes a regular language. It consists of four components, which are as follows −

G = (N, E, P, S)

Where,

• N: finite set of non-terminal symbols,

• E: a finite set of terminal symbols,

• P: a set of production rules, each of one is in the forms

• S → aB

• S → a

• S → ∈,

• S ∈ N is the start symbol.

The above grammar can be of two forms −

• Right Linear Regular Grammar

• Left Linear Regular Grammar

Now, let us see the steps to convert left linear grammar to right linear grammar −

Example 1

Consider a left linear grammar as given below −

S→ Sa|Abc
A→ Sa|Ab|a

Step 1 − We will convert the given left linear grammar to finite automata.

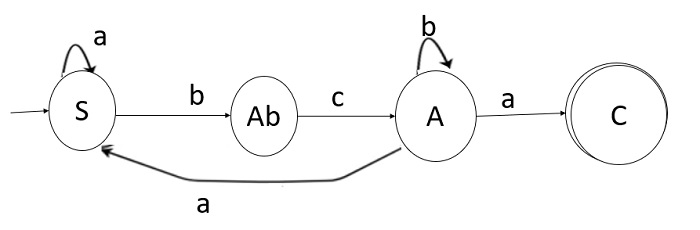
Step 2 − We will now interchange the initial and final state.

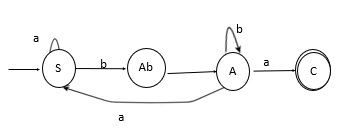
Step 3 − Now we will reverse the direction of all transactions.

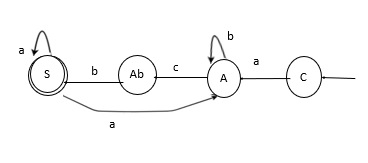
Step 4 − We will construct the regular grammar for the above finite automata which will be right linear grammar, as shown below −

C→aA
A→bA|cb
S→aS

Example 2

Consider another example

The given left linear grammar is −

S→S10|S11|B|e
B→B0|0

First eliminate non-deterministic of grammar

S→SA|B|e
A→10|11
B→B0|0

So, the right linear grammar is −

S→BS’|S’
S’→e|10S’|11S’
B→0B’
B’→0B’|e

Bhanu Priya

e

Updated on: 14-Jun-2021

7K+ Views

Kickstart Your Career

Get certified by completing the course

Get Started